一、系统方案

随着计算机及其网络应用的日益普及，尤其是互联网应用的迅猛发展，计算机及其网络系统的安全管理问题日显突出，各种非法的计算机及网络入侵事件频频发生。据统计，网络入侵的70%~80%来自于网络内部，因此加强对计算机使用者身份的监督和管理，防止合法用户的越权和恶意访问以及非法用户的非法访问都显得十分重要。

那么，我们怎样加强对计算机使用者身份的监督和管理呢？

首先，传统的密码技术是最常用的用户访问控制手段，但密码又比较容易遗失或被破解。

于是，人们提出了多个基于各种生物特征的用户身份认证方法，是的身份认证智能化。这些生物特征包括：指纹、虹膜、面部、声音、掌形（纹）等。但基于这些生物特征的用户身份认证方法均需要额外价格不菲的硬件设备（其价格从数百美元到数万美元不等），这也就使得基于这些生物特征的用户身份认证方法无法得到广泛的应用。

为利用现有普通电脑硬件，完成基于生物特征的用户身份认证，人们提出了基于用户击键特征来进行用户身份认证的方法，该方法利用用户输入口令时的击键压力、击键节奏等所构成的用户生物特征，来进行用户身份的认证工作。用户由于不同的生理特点和习惯，在使用键盘时存在击键力度、键盘熟练程度等明显差异（类似于笔迹、指纹）。

受智能密码的启发，即不同用户的键盘使用习惯、特征存在差异，我们提出一种将用户键盘使用特征和神经网络技术相结合的用户身份监督、管理方法。本系统就是利用这种差异提取特征量， 建立模型， 实现对用户身份的辨别和监控。

目前，国内外有关的基于用户击键生物特征进行身份认证研究的公开报道并不多：Dunn认为击键时延符合正态分布并使用了距离分类法；Monrose 和Rubin提出了一种基于K近邻聚类方法的算法；Kacholia和Pandit提出了一种基于启发式聚类的算法，但并没有给出聚类算法的细节；Ru 和Eloff及Tapiador 和Sigüenza尝试了模糊数学的方法；朱明等人也提出了基于示例学习的方法对用户身份的真伪进行判断，曲维光和宋如顺等人则利用对神经网络进行训练来区分不同的用户，Monrose 等人将这一技术用于强化用户身份验证。但是，他们的研究都是基于软件层面的，而且采样数据也很有限。

我们提出的智能安全键盘将压力传感器加入传统键盘中，旨在利用已有的用户名和密码，通过用户特定的击键特征，即按键时间长短、时间间隔和压力三个参数，来判定某一击键序列是否为某特定用户的行为，进而对用户身份的真伪进行判断识别，以此来强化身份验证的效果，防止密码被他人非法使用，加强对计算机使用者身份的监督和管理，使键盘操作更安全，从而达到信息安全的目的。

二、实现方案

（一）理论基础

根据一个简化的统计，人脑由百亿条神经组成，每条神经平均连结到其它几千条神经。通过这种连结方式，神经可以收发不同数量的能量。神经的一个非常重要的功能是，它们对能量的接受并不是立即作出响应，而是将它们累加起来，当这个累加的总和达到某个临界阈值时，将自己的那部分能量发送给其它的神经。大脑通过调节这些连结的数目和强度进行学习。尽管这是个生物行为的简化描述。但同样可以充分有力地被看作是神经网络的模型。

阈值逻辑单元（Threshold Logic Unit，TLU）

理解神经网络的第一步是从对抽象生物神经开始，并把重点放在阈值逻辑单元(TLU)这一特征上。一个TLU是一个对象，它可以输入一组加权系数的量，对它们进行求和，如果这个和达到或者超过了某个阈值，则输出一个量。用符号标注这些功能，首先，输入值以及它们的权系数分别记为X1,X2,...,Xn和W1,W2,...,Wn。接着，求和计算出的Xi*Wi，产生了激发层a，换一种方法表示：

a = (X1 * W1)+(X2 * W2)+...+(Xi * Wi)+...+ (Xn * Wn)

阈值称为theta。最后，输出结果y。当a>=theta时y=1，反之y=0。输出可以是连续的，因为它也可以由一个squash函数s（或 sigma）判定，该函数的自变量是a，函数值在0和1之间，y=s(a)。

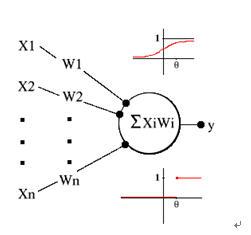
阈值逻辑单元，带有 sigma 函数（顶部）和 cutoff 函数（底部）

TLU 会分类，假设一个TLU有两个输入值，它们的权系数等于1，theta值等于1.5。当这个 TLU 输入<0,0>、<0,1>、<1,0>和<1,1>时，它的输出分别为0、0、0、1。TLU将这些输入分为两组：0组和1组。

TLU 的学习原理

神经网络的学习机制是模仿大脑调节神经连结的原理。TLU通过改变它的权系数和阈值来学习。当SUM(Xi*Wi)>=theta时TLU在临界点时输出的是1而不是0，临界点是出现在SUM(Xi*Wi)+(-1*theta)>=0的时候。所以，我们可以把-1看成一个常量输入，它的权系数theta在学习的过程中进行调整。这样，当SUM(Xi*Wi)+(-1*theta)>=0时，y=1，反之y=0。

在学习过程中，神经网络输入一系列需要分类的术语示例和它们的正确分类或者目标。

这样的输入可以看成一个向量：<X1,X2,...,Xn,theta,t>，这里t是一个目标或者正确分类。神经网络用这些来调整权系数，其目的使学习中的目标与其分类相匹配。更确切地说，这是有指导的学习，与之相反的是无指导的学习。前者是基于带目标的示例，而后者却只是建立在统计分析的基础上。权系数的调整有一个学习规则，一个理想化的学习算法如下所示：

fully_trained = FALSE

DO UNTIL (fully_trained):

fully_trained = TRUE

FOR EACH training_vector = <X1, X2, ..., Xn, theta, target>::

# Weights compared to theta

a = (X1 * W1)+(X2 * W2)+...+(Xn * Wn) - theta

y = sigma(a)

IF y != target:

fully_trained = FALSE

FOR EACH Wi:

MODIFY_WEIGHT(Wi) # According to the training rule

IF (fully_trained):

BREAK

学习规则有很多，通过对收集的大量资料的研究分析，我们发现，有一条似乎合理的规则是基于这样一种思想，即权系数和阈值的调整应该由分式(t-y)确定。这个规则通过引入学习率alpha(0<alpha<1)完成。Wi中的更改值等于(alpha*(t-y)*Xi)。当alpha趋向于0时，神经网络的权系数的调整变得保守一点；当alpha趋向于1时，权系数的调整变得激进。使用这个规则的神经网络称为感知器，这个规则被称为感知器学习规则。

关于 delta 规则

delta 规则是基于梯度降落这样一种思路的。在权系数的调整中，神经网络将会找到一种将误差减少到最小的权系数的分配方式。

将我们的网络限制为没有隐藏节点，但是可能会有不止一个的输出节点，设p是一组学习中的一个元素，t(p,n)是相应的输出节点n的目标。设y(p,n)由以上提到的squash函数s决定，这里a(p,n)是与p相关的n的激活函数，或者用(p,n)=s(a(p,n))表示为与p相关的节点n的squash过的激活函数。为网络设定权系数（每个Wi），也为每个p和n建立t(p,n)与y(p,n)的差分，这就意味着为每个p设定了网络全部的误差。因此对于每组权系数来说有一个平均误差。但是delta规则取决于求平均值方法的精确度以及误差。对于每个Wi，平均误差定义如下：

sum = 0

FOR p = 1 TO M: # M is number of training vectors

FOR n = 1 TO N: # N is number of output nodes

sum = sum + (1/2 * (t(p,n)-y(p,n))^2)

average = 1/M * sum

delta规则就是依据这个误差的定义来定义的。因为误差是依据那些学习向量来说明的，delta规则是一种获取一个特殊的权系数集以及一个特殊的向量的算法。而改变权系数将会使神经网络的误差最小化。任何Wi发生的变化都如下所示：alpha*s'(a(p,n))*(t(p,n)-y(p,n))*X(p,i,n)。

X(p,i,n)是输入到节点n的p中的第i个元素，alpha是已知的学习率。最后s'(a(p,n))是与p相关的第n个节点激活的squashing函数的变化（派生）率，这就是delta规则，并且当alpha非常小的时候，权系数向量接近某个将误差最小化的向量。用于权系数调节的基于delta规则的算法就是如此。

梯度降落（直到误差小到适当的程度为止）如下：

step 1: for each training vector, p, find a(p)

step 2: for each i, change Wi by:

alpha * s'(a(p,n)) * (t(p,n)-y(p,n)) * X(p,i,n)

delta规则算法总是在权系数上调整，而且这是建立在相对输出的激活方式上，不一定适用于存在隐藏节点的网络。

反向传播

反向传播这一算法把支持delta规则的分析扩展到了带有隐藏节点的神经网络。当输出节点从隐藏节点获得输入，网络发现出现了误差，权系数的调整可以通过一个算法来找出整个误差是由多少不同的节点造成的，具体方法如下：

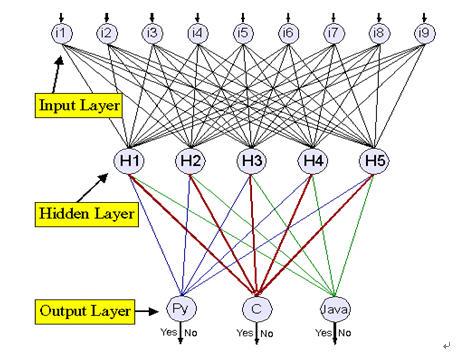
“代码识别”反向传播的神经网络

反向传播算法同样来源于梯度降落原理，在权系数调整分析中的唯一不同是涉及到t(p,n)与y(p,n)的差分。通常来说Wi的改变在于：

alpha * s'(a(p,n)) * d(n) * X(p,i,n)

其中d(n)是隐藏节点n的函数。一方面，n影响输出节点越多，n造成网络整体的误差也越多。另一方面，如果输出节点影响网络整体的误差越少，n对输出节点的影响也相应减少。这里d(j)是对网络的整体误差的基值，W(n,j)是n对j造成的影响，d(j)*W(n,j)是这两种影响的总和。但是n几乎总是影响多个输出节点，也许会影响每一个输出结点，这样，d(n)可以表示为：SUM(d(j)*W(n,j))

这里j是一个从n获得输入的输出节点，联系起来，我们就得到了一个学习规则。

第1部分：在隐藏节点n和输出节点j之间权系数改变，如下所示：

alpha * s'(a(p,n))*(t(p,n) - y(p,n)) * X(p,n,j)

第2部分：在输入节点i和输出节点n之间权系数改变，如下所示：

alpha * s'(a(p,n)) * sum(d(j) * W(n,j)) * X(p,i,n)

这里每个从n接收输入的输出节点j都不同。关于反向传播算法的基本情况大致如此。

将Wi初始化为小的随机值。

使误差小到适当的程度要遵循的步骤如下：

第1步：输入学习向量；

第2步：计算隐藏节点的输出；

第3步：在第2步的基础上计算输出节点的输出；

第4步：计算第3步所得的结果和期望值之间的差；

第5步：把第4步的结果填入学习规则的第1部分；

第6步：对于每个隐藏节点n，计算d(n)；

第7步：把第6步的结果填入学习规则的第2部分。

通常把第1步到第3步称为正向传播，把第4步到第7步称为反向传播。

至此，我们已经成功地通过神经网络算法对用户需要分类的术语示例进行了正向学习，对用户需要验证的数据进行了识别，并且对经过验证的数据进行了反向传播学习。

（二）实现原理

使用Xilinx Spartan 3E Starter-kit的开发板开发应用程序的过程大致分为两部分——硬件和软件。

⒈硬件部分。借助Xilinx Platform Studio 9.1i with SP2（一下简称为XPS）良好的界面和易用性，我们借助其自带的IP核实现大部分开发板上设备的驱动，但是由于我们的项目要用到PS/2键盘、A/D转换器以及CC2420射频板等相应的IP核并没有附带在XPS中的设备，因此我们正在完成这些设备的IP核的设计，以便搭起我们所需要的硬件平台。

⒉软件部分。通过XPS中附带的Xilinx Platform Studio SDK（以下简称为XPSSDK）组件，我们使用C语言完成我们的项目的核心部分的设计。XPSSDK的外壳实际上使用的是开源软件Eclipse，其友好的界面可以极大方便我们的项目的开发。软件核心部分分为信号处理模块和密码处理模块。其中，信号处理模块采用神经网络算法，密码处理模块采用混沌算法。

⑴信号处理模块

信号采集部分主要采集三个系数：按键时间长短、按键时间间隔和力感模拟信号。其中前两个系数可以通过按键产生的通码和断码得到（每个通码和下一个断码之间构成一个按键时间长短，每个断码与下一个通码之间构成一个按键时间间隔），力感模拟信号可以通过绑定在每个按键下面的力度传感器采集到。

若用TH(i)表示第i个键按下的持续时间(Hold-time，即按键时间长短),则TH(i)=Trelease(i) -Tpress(i),Tpress(i)表示第i个键的按下时刻,Trelease(i)表示第i个键抬起的时刻。令TL(i,i+1)表示连续敲击第i个键和第i+1个键的时间间隔。则TL(i,i+1)=Tpress(i+1) -Trelease(i)。对于我们采集到的力感系数，每按键一次产生一个相关力度模拟信号，经Spartan 3E开发板上的A/D转换器将其转化为数字信号，得到相应的力感值TM(i)。若用户口令由n个字符组成,则最后我们得到一个3n-1维的信号采集特征向量[TH(1), TM(1),TL(1,2),TH(2), TM(2),TL(2,3),TH(3), TM(3),……,TL(n-1,n),TH(n) , TM(n)]。

然后我们将这些特征向量作为BP神经网络的输入层神经元，使用BP算法通过一边向后传播误差,一边修正误差的方法来不断调节网络参数(权值或阈值),以实现或逼近所希望的输入输出映射关系，最后得以对合法用户的身份进行辨别。

BP算法的学习过程如下:

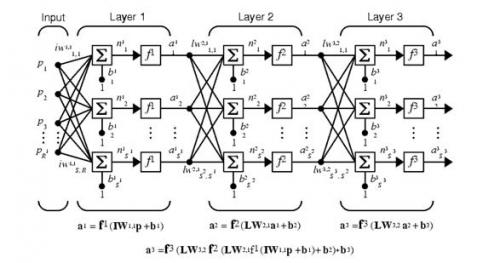
①正向传播：输入信息从输入层经隐含层逐层处理，并传向输出层，每层神经元的状态只影响下一层神经元的状态（如下图所示）。

②反向传播：如果在输出层不能得到期望的输出，则转入反向传播，将误差信号沿原来的连接通路返回，通过修改各层神经元的权值，使误差信号最小。

BP算法的主要步骤如下：

①置所有权值为较小的随机数；

②提供训练集，给定输入向量X=(x1,x2,……,xm)和期望的目标输出向量D=(d1,d2,……,dn)；

③前向计算，计算实际输出，计算隐含层,输出层各神经元的输出： ；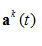

④对输出层计算δ： ；

⑤从后向前计算各隐层δ： ；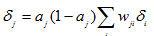

⑥计算并保存各权值修正量： ；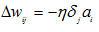

⑦修正权值： ；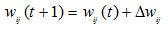

⑧判断是否收敛，如果收敛则结束，不收敛则转至(3)重复计算，直到误差Ep满足要求。

本系统实现设计的BP网络考虑到用户的口令长度通常为8~16个，对应生成的特征的维数为23-47维，因此网络的输入节点数定为20~50，可依据口令长度选择。隐含层节点数需要在实现过程中不断模拟训练进行确定，以使判别效果达到最佳。

⑵密码处理模块

设混沌序列为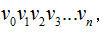，其中，

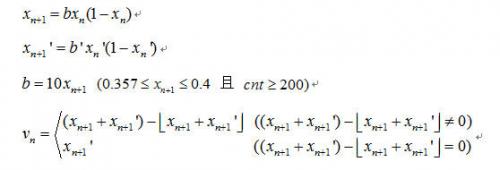
考虑到这四个值在PS/2总线上传输带来的安全性的问题，我们决定让其在密码处理模块和PC机端分别生成，生成函数如下：

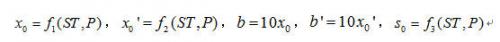
（三）硬件框图

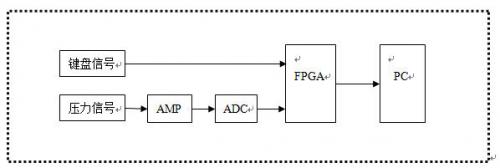
在硬件框图中，键盘信号包括按键时间长短、按键时间间隔和密码明文三个信号，该信号通过RS232总线传送至FPGA。由于FPGA的ADC对电压的范围有要求，压力信号先通过AMP进行放大处理后，再通过ADC转换成数字信号后再传送至FPGA。在FPGA上，信号处理模块运用神经网络算法对采集的信号样本进行处理，对于通过神经网络的信号样本，通过密码处理模块的混沌算法对密码进行加密后，再通过RS232总线送至PC。在PC端，密码实际上为密码原文经混沌加密以后的密文。

三、设计与实现的功能

1．安全性。以应用为基础，以神经网络为核心，以混沌算法辅助完成基于有限学习正例集合的正反例识别。通过采集用户击键习惯相关系数，采用BP神经网络算法动态学习、判别合法用户特征，再通过混沌算法对密码进行加密处理，实现高效、高用户辨别能力的身份认证。

2．多用户支持。利用FPGA的大量数据处理能力，可以方便地实现采样数据与相关数据库中大量数据的迅速比对。

3．力感识别。通过对相关资料的学习，我们发现目前关于用户特征信息采样的研究工作都是基于击键时间长短和时间间隔的，我们通过力度传感设备将用户击键力度数字化之后，作为用户特征信息的一个方面，进行比对验证和学习。

4．密码键盘与普通键盘的切换。单用户应用环境中，可以通过硬件开关屏蔽传感器不进行相应数据处理而实现密码键盘与普通键盘的切换。

5．成本低廉。对用户的眼底图像、指纹、头像等的识别均需要特殊的硬件设备，且有些设备价格相当昂贵，不利于系统的实施和推广。而除了力感识别所需的压力传感器以外，了解用户的击键节奏不需要添加其他硬件，是各种生物特征用户认证技术中代价较小的一种，易于为用户所接受。

四、性能指标

在系统检测方面，我们将分别模拟单用户和多用户应用环境，采集相关数据，通过以下两个评价指标，检测系统的性能：

1．检测率（Detection Rate，DR）：被检测到的假冒样本的数量和测试集中总的假冒样本的数量的比率；

2．虚警率（False Positive Rate，FPR）：正常样本数据被误检为假冒样本的数量和测试集中总的正常样本的数量的比率。

五、系统特色

本系统最大的特色在于采用了神经网络算法，智能地对用户击键特征进行学习和识别。

人工神经网络模型主要考虑网络连接的拓扑结构、神经元的特征、学习规则等。目前，已有近40种神经网络模型，其中有反传网络、感知器、自组织映射、Hopfield网络、波耳兹曼机、适应谐振理论等。根据连接的拓扑结构，神经网络模型可以分为：(1)前向网络 网络中各个神经元接受前一级的输入，并输出到下一级，网络中没有反馈，可以用一个有向无环路图表示。这种网络实现信号从输入空间到输出空间的变换，它的信息处理能力来自于简单非线性函数的多次复合。网络结构简单，易于实现。反传网络是一种典型的前向网络。(2)反馈网络 网络内神经元间有反馈，可以用一个无向的完备图表示。这种神经网络的信息处理是状态的变换，可以用动力学系统理论处理。系统的稳定性与联想记忆功能有密切关系。Hopfield网络、波耳兹曼机均属于这种类型。

学习是神经网络研究的一个重要内容，它的适应性是通过学习实现的。根据环境的变化，对权值进行调整，改善系统的行为。由Hebb提出的Hebb学习规则为神经网络的学习算法奠定了基础。Hebb规则认为学习过程最终发生在神经元之间的突触部位，突触的联系强度随着突触前后神经元的活动而变化。在此基础上，人们提出了各种学习规则和算法，以适应不同网络模型的需要。有效的学习算法，使得神经网络能够通过连接权值的调整，构造客观世界的内在表示，形成具有特色的信息处理方法，信息存储和处理体现在网络的连接中。

本系统采用的神经网络算法的学习方式为监督学习。我们将训练样本的数据加到网络输入端，同时将相应的期望输出与网络输出相比较，得到误差信号，以此控制权值连接强度的调整，经多次训练后收敛到一个确定的权值。当样本情况发生变化时，经学习可以修改权值以适应新的环境。

人工神经网络特有的非线性适应性信息处理能力，克服了传统人工智能方法对于直觉，如模式、语音识别、非结构化信息处理方面的缺陷，使之在神经专家系统、模式识别、智能控制、组合优化、预测等领域得到成功应用。人工神经网络与其它传统方法相结合，将推动人工智能和信息处理技术不断发展。近年来，人工神经网络正向模拟人类认知的道路上更加深入发展，与模糊系统、遗传算法、进化机制等结合，形成计算智能，成为人工智能的一个重要方向，将在实际应用中得到发展。将信息几何应用于人工神经网络的研究，为人工神经网络的理论研究开辟了新的途径。神经计算机的研究发展很快，已有产品进入市场。光电结合的神经计算机为人工神经网络的发展提供了良好条件。

神经网络在这个领域中有很多优点，使得它越来越流行。它在类型分类/识别方面非常出色。神经网络可以处理例外及不正常的输入数据，这对于很多系统都很重要（例如雷达及声波定位系统）。很多神经网络都是模仿生物神经网络的，即是他们仿照大脑的运作方式工作。神经网络也得助于神经系统科学的发展，使它可以像人类一样准确地辨别物件而有电脑的速度！

基于软件实现的神经网络也有些不好的地方。这通常都是因为缺乏足够强大的硬件。神经网络的力量源自于以并行方式处理资讯，即是同时处理多项数据。因此，要一个串行的机器模拟并行处理是非常耗时的。但是，我们将该算法转移到硬件板上来实现，避免了这一缺陷。

本系统的另一个特色点在于对密码的混沌加密。

混沌理论是一种迅速发展的新科学，致力于研究复杂的、非线性的、动态的系统。混沌理论不是关于无序的理论，虽然从字面上看起来是这样。相反，它可以看作是一种更好地理解秩序的方法。

混沌系统具有三个关键要素：一是对初始条件的敏感依赖性；二是临界水平，这里是非线性事件的发生点；三是分形维，它表明有序和无序的统一。混沌系统经常是自反馈系统，出来的东西会回去经过变换再出来，循环往复，没完没了，任何初始值的微小差别都会按指数放大，因此导致系统内在地不可长期预测。

混沌是一个难以精确定义的数学概念。一般而言，“混沌”是指由确定性方程描述的动力学系统中表现出的非确定性行为，或称之为确定的随机性。“确定性”是因为它由内在的原因而不是外来的噪声或干扰所产生，而“随机性”是指其不规则的、不能预测的行为，只可能用统计的方法描述。混沌动力学系统的主要特征是其状态对初始条件的灵敏依赖性，混沌反映其内在的随机性。混沌理论是指描述具有混沌行为的非线性动力学系统的基本理论、概念、方法，它把动力学系统的复杂行为理解为其自身与其在同外界进行物质、能量和信息交换过程中内在的有结构的行为，而不是外来的和偶然的行为，混沌状态是一种定态。混沌动力学系统的定态包括：静止、平稳量、周期性、准同期性和混沌解。混沌轨线是整体上稳定与局部不稳定相结合的结果，称之为奇异吸引子。一个奇异吸引子有如下一些特征：(1)奇异吸引子是一个吸引子，但它既不是不动点，也不是周期解；(2)奇异吸引子是不可分割的，即不能分为两个以及两个以上的吸引子；(3)它对初始值十分敏感，不同的初始值会导致极不相同的行为。

我们正是利用混沌算法的以上特性，结合基于用户按键特征的混沌初值，生成相应的混沌序列对密文进行处理，从而极大地加强了本系统的安全性。

六、系统测试

（一）测试方案

取10人，每两人一组，共5组。10个用户使用同一台电脑和键盘，要求他们根据自身的输入习惯使用，不要刻意模仿，依次进行如下实验。

实验一：10个用户分别按自己正常的输入习惯输入自己设定的6位密码8次，各个用户分别形成自己的训练样本。经过神经网络学习后，各用户再分别输入自己预定的6位密码，测试本系统的虚警率。

实验二：各用户按自己的正常输入习惯分别输入错误的6位密码，测试本系统的检测率。

实验三：每组用户分别用该组另一用户的6位密码尝试登录本系统，测试本系统的检测率。