集成电路的开发人员再也不能如以前那般准确地预测未来了。 理论上来说,一个提交生产的新集成电路设计会有明确的规格,其性能特征也会有一个准确的描述。但实际情况并非如此,通常生产过程开始之后,开发人员还是会对设计增加一些新的要求。
集成电路生产团队一般都会想方设法满足开发人员的这些后续要求。但是,他们还是会碰到很棘手的情况,比如,开发人员通常会要求改变由生产测试部门制定的射频滤波器的特性描述方法。这会引起测试软件代码的一系列变化。这样不仅会耽误测试进程,延缓芯片设计定型的进度,并且有可能会使测试代码产生错误,因为整个生产团队经常处于加快制造过程的巨大压力下,可能没有足够的时间用于全面调试测试代码。
因此,奥地利微电子公司的测试工程团队试图研究一种新的方法来对射频滤波器进行特征描述,以此解决上述问题。团队的策略是开发一个标准的测试程序,它可同时用于特征描述和生产过程中。此外,该程序还可进行一些简单的修改,以适应各种不同规格的集成电路的要求。这个新的标准程序被放置在一个测试代码库中,使基本的测试IP能得到反复再利用。
测试团队选择的方法是使用一个线性调频器,扫描滤波器的频率范围,通过单次测量可描述滤波器的特性。
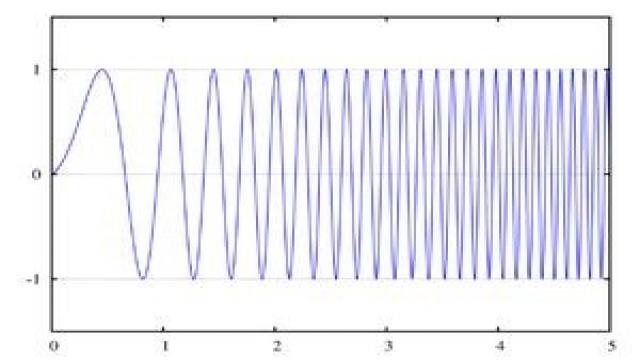
图1:线性调频
团队考虑到使用多频声来描述滤波器特性的可能性。但是,该方法并不适合输入功率灵敏度较低的设备。如果要使用多频声,各个频率分量必须根据频率总数被划分,以此保证整体的峰值系数低于最大输入功率。如果不这么做,单个频率之间会相互影响引起互调失真,干扰频率扫描的结果。
如何构建一个线性调频器
在一个线性调频中,信号的瞬时频率呈线性增加趋势,并且没有跳频(如图1所示)。但考虑到任意波形发生器(AWG)中有限的内存大小,测试工程师必须构建一个离散形的线性调频器。线性调频的公式如下:f(t) = f0 + kt。其中,f0代表起始频率(时间t=0),k代表频率增加率或调频转换速率。
当线性调频的扫描过程完成并且获得扫描结果后,该新方法还要求对集成电路设计者想要进行特征描述的滤波器进行关键参数的提取:提取幅值响应,即过滤器的3dB点、10dB点以及滤波器的带宽。有时,也需要提取其它一些参数,如相位响应和群延迟。
为了在数字信号处理器中构建线性调频信号,我们必须了解以下这些参数:
• 测量带通滤波器的转角频率时应该达到怎样的精确度?
• 测量设备中的哪些特性有利于测量工作的展开?存储深度、最大采样频率,还是波形拼接?
• 滤波器的转角频率和带宽是多少?
随着最新测试码开发工具中syntax的出现,在数字信号处理器中构建线性调频波形图变得非常简单。通常情况下,syntax提供一个选项,它可根据样本数、采样频率、数组大小、相位延迟以及Sinx/x 修正,使用内置函数构建一个正弦波形。通过将该测试码放入一个回路,并线性地增加bin数,将会产生一组呈线性增加趋势的音频波形。只要根据取样原理确保该过程的连贯性,那么这些波形就会拼接在一起,并形成一个离散的线性调频信号。
若没有产生单个波形的内置函数,那么我们可以使用取样原理。取样原理要求在数组中M呈线性增加,并且要求快速傅里叶变换呈逆向运作,如:
取样原理方程式:Fs/Ft = N/M
傅里叶频率计算方程式:Ff = Fs/N
一旦逆向快速傅里叶变换完成,每个时域的数据必须相互拼接,以此产生一个数组。该数组的尺寸大小相当于样品数乘以音频数。在这里,我们必须注意确保数组小于任意波形发生器的内存。
奥地利微电子公司为晶圆代工客户开发的线性调频测试中,最困难的是测试带宽最窄的滤波器,它的中心频率为40kHz,带宽约为80kHz。3dB点的测量精度需在5kHz之内。在这样的情况下,我们构建了一个线性调频器,它包含100个频率分辨率为1kHz的离散频率。线性调频信号初始频率为1kHz终止频率为100kHz(如图2)。
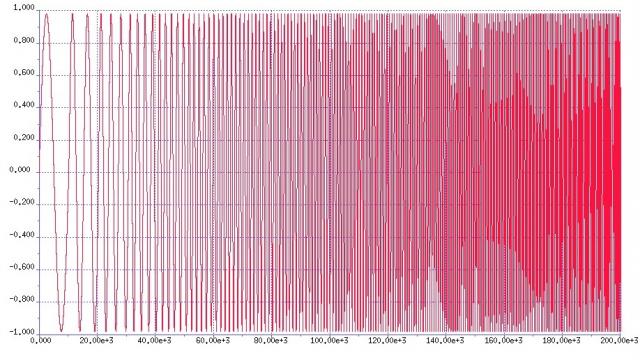
图2:归一化的线性调频信号
通过分析在频率范围内的信号特征我们可以知道频率响应是否符合预期的1kHz至100kHz的平坦的频谱特征,因为在这个扫描过程中,信号幅度保持不变。通过对线性调频信号进行快速傅里叶变换我们可以看到以下的频率响应(如图3); 一个平坦的频率响应可以提供一个新的频率范围,它能使相对测量值(如3dB值)变得更为准确。
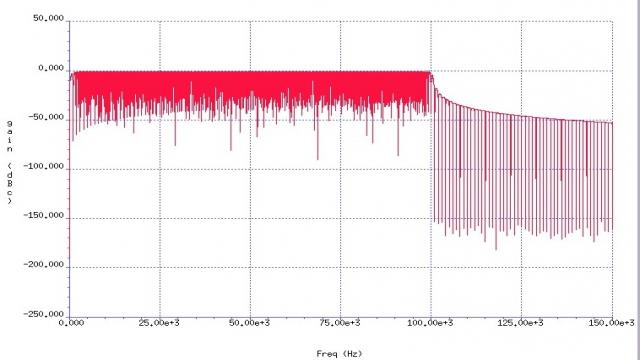
图3:线性调频信号的快速傅里叶变换
信号产生后的下一步是测量。为了方便比较,采样的点数和采样频率应与信号生成时一致。图4显示了利用单次量测获取的带通滤波器的曲线特征。通过使用数字信号处理器分析该结果,我们便可以计算出3dB点值。
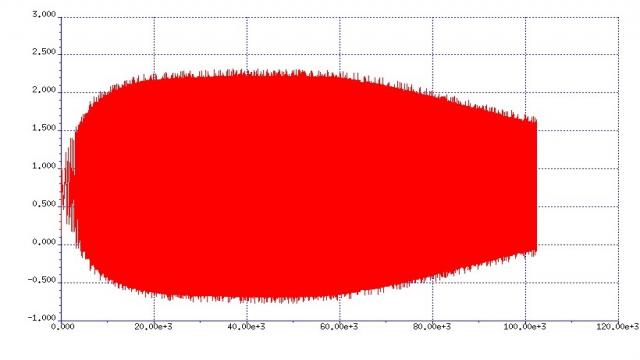
图4:单次量测获取时间域
在完成对所获取的数组进行快速傅里叶变换后(如图5),过滤器的3dB点值便通过使用数字信号处理按照以下顺序准确的计算出来:
1) 取数组平滑区段的平均值,这可以确保数组没有急剧的变化。
2) 将获取的数组由伏特转为dBc。
3) 在整个数组中增加3dB值,此时,负3dB点的数值变为0dB。
4) 提取具有极小变量的数组段
5) 对所提取的数组段进行极值分析,确定低通3dB点的位置。
6) 颠倒数组段,将滤波器的高通部分放置在数组的起始位置。
7) 对颠倒的数组段进行极值分析,确定高通3dB点的位置。在这里必须记住,这个数值必须从所有点中减去。
8) 通过傅里叶频率分析法增加数组的位置,得到的结果是正负3dB点的频率值。
9) 两个3dB点的频率值相减就能得到滤波器的带宽。
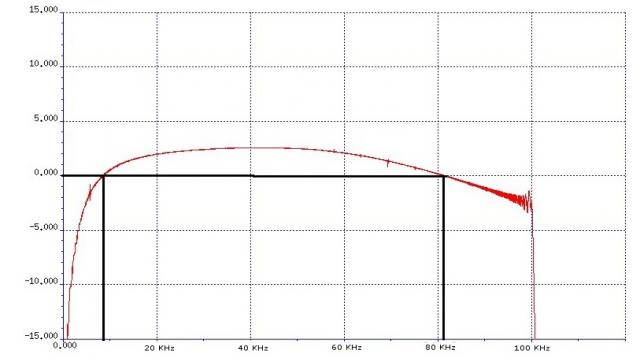
图5:图4中数组的频域特性
如果上述测试方法是健壮的,那么从实验室获得的结果与生产测试人员获得的结果之间会有一个确切的相关性。这里列出的一个例子表明,上限截止频率的测量结果一般都稳定在84.3kHz,标准偏差为36Hz(如图6)。
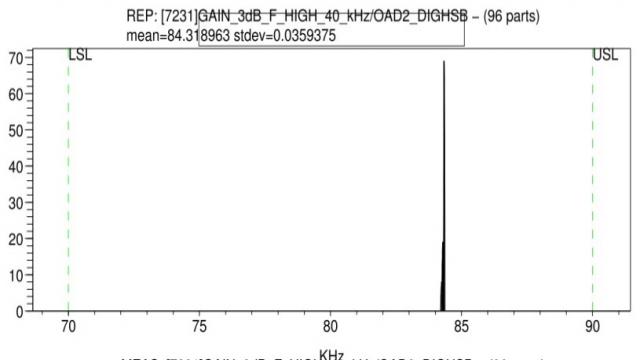
图6:40kHz带通滤波器上限截止频率的重复性
图7表明,实验结果和生产测试人员获得的结果极其接近。结合稳定性的数据,表明上述的测试方案是RF芯片生产测试的理想方法。
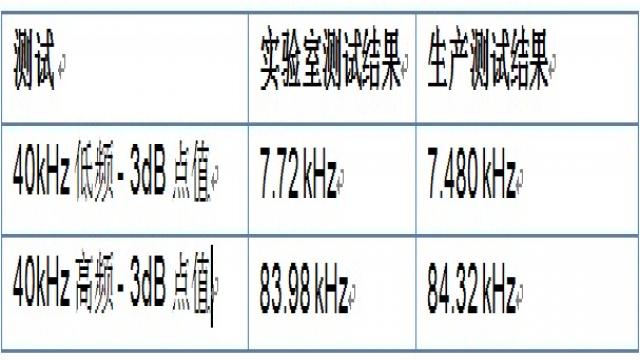
图7:40kHz过滤器实验结果的相关性
文章开篇介绍了奥地利微电子公司研究该测试方法的目的是为了找到一种测试方案,能使IP在多个测试项目中反复使用。重复使用的策略是建立在一个归一化的波形,该波形以1kHz的增速由1kHz增长至100kHz。由于归一化频率为1kHz,按比例增加任意波形发生器的采样频率就可以方便地改变波形的分辨率。
例如,采用1kHz的傅里叶频率的线性调频来测试一个40kHz的过滤器,它的3dB值要求适度精确。同样的一个波形,如果它已经被放置在任意波形发生器的存储器里,通过增加Fs,这个波形便可用于其它滤波器的测试,以此节省任意波形发生器的内存。例如,某应用中滤波器的中心频率为550kHz,高频部分的3dB点约为800kHz。Fs乘以10产生傅里叶频率为10kHz而非1kHz的波形;线性调频将从10 kHz开始并在1MHz结束。如图8所示,这种测试方法产生相关性较高的测试结果。
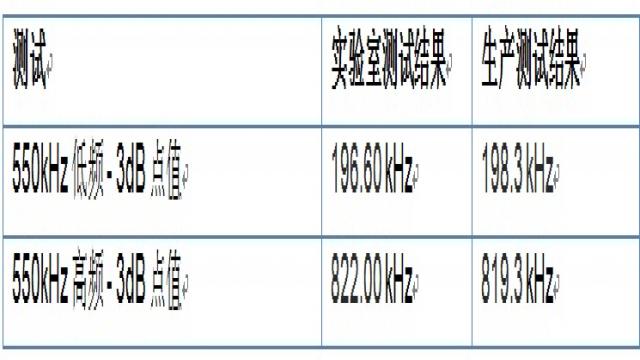
图8:550kHz滤波器实验结果的相关性
通过将测试结果和源波形进行比较我们可以看到,误差比源波形的分辨率要小(分辨率为10kHz,误差为3kHz)。这是因为选取的数组段以与插值类似的方式运作。
使用一个合适的傅里叶频率分辨率的线性调频信号可以得到一个好的相关性,因此可用于对芯片进行特征描述。采用这种方法设计的信号可产生归一化的波形,因此通过改变任意波形发生器的采样频率,能以更低的分辨率获得更高的频率。这样一来,这种方法就显得非常灵活,可适用于多种不同设备。