机车车辆企业是典型的订单式生产企业，面对全球经济一体化，客户需求个性化以及产品交货高速化的经济时代，机车车辆行业面临着快速响应客户需求、缩短产品交货期、提高产品质量和改进产品服务的压力。为了在激烈的市场竞争中求得生存和发展，企业需要从生产调度环节进行优化。生产调度是制造系统的一个研究热点，调度的任务是根据生产目标和约束，为每一个对象确定具体的加工路径、时间、机器和操作等，优良的调度策略对于缩短产品的生产时间，降低成本有着极大的作用。

订单生产调度问题属于一类NP-hard组合问题，因此寻找具有多项式复杂性的最优算法几乎是不可能的。传统的启发式算法、智能模拟退火算法、禁忌算法、神经网络法等算法其共性是对生产线优化问题寻求满足实际需要的近似解或满意解，但都是局部寻优的方法。而各种基于统计优化的方法诸如模拟退火法、遗传算法等，提供了一种解决调度优化问题的新途径，但也存在着一定程度的枚举，一般来说收敛到最优解较慢，并且对于判断解的最优性也很困难。将遗传算法与优化算法结合起来对解决订单生产调度问题具有较高的性能。

1 混合遗传算法

1.1 遗传算法

遗传算法由于其运算的简易性和解决问题的高效性而被广泛应用于众多的领域。理论上已经证明，遗传算法能从概率的意义上以随机的方式寻求到问题的最优解。但是另一方面，应用实践表明，在遗传算法的应用过程中也会出现一些不尽如人意的问题，这些问题主要表现为：容易产生早熟现象、局部寻优能力较差等。并且一般来说，对很多问题，基本遗传算法的求解效果往往不是解决这个问题的最有效的方法，它比起专门针对该问题的知识型启发算法的求解效率要差，虽然这种知识型启发算法并保证不了一定能够找到问题的全局最优解。另外，遗传算法也无法避免多次搜索同一个可行解的情况，这也是影响遗传算法运行效率的一个重要因素。

1.2 混合遗传算法

梯度法、爬山法、模拟退火算法、列表寻优法等一些优化算法却具有很强的局部搜索能力，而遗传算法由于其运算的简易性以及另一些含有问题与相关知识的启发式算法的运行效率也比较高。因此可以预计，在遗传算法的搜索过程中融合这些优化方法的思想，构成一种混合遗传算法是提高遗传算法运行效率和求解质量的一个有效手段。

混合遗传算法是在标准遗传算法中融合了局部搜索算法的思想，其特点主要体现在以下两个方面：

（1）引入了局部搜索过程。基于群体中各个个体所对应的表现型，进行局部搜索，从而找出各个个体在目前的环境下所对应的局部最优解，以便达到改善群体总体性能的目的。

（2）增加了编码变换操作过程。对局部搜索过程所得到的局部最优解，再通过编码过程将它们变化为新的个体，以便能够以一个性能较优的新群体为基础来进行下一代的遗传进化操作。

2 机车车辆业面向订单生产调度模型

订单生产调度问题中存在着多种优化目标或者综合优化目标，调度问题的优化目标通常从生产的成本和生产的时间两个方面来考虑。从生产成本方面来考虑，其优化目标有：制品最少、库存最少、设备利用率最高等；从生产时间方面来考虑，其优化目标有：最小完成时间、最大程度满足交货期、最小流动时间和最小等待时间等。这两个方向的优化目标之间彼此不是相互孤立的，其中的许多具体目标之间联系非常密切，有的相互促进，有的相互冲突，也有的毫无联系。本算法采用以总加工时间最小为目标，具体表示为：

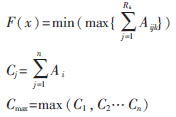
其中：Rk表示需要在设备k上加工的总工序数；Aijk表示第i个工件的第j道工序在设备k上完成加工所需要的时间。这个时间包括开始加工此道工序之前的等待时间Wijk和从开始加工到完成此道工序的所需时间Nijk;Cj表示订单j的生产时间是订单j中包括的所有部件全部完成的时间总和；Cmax为所有订单在并行生产的情况下，最大完工时间，即各个订单完成时间最晚的订单的完成时间；目标函数F（x）的目的是使得最长需要时间尽可能地短。这样，经过算法的多次迭代后就可以生成调度的近似最优解，得到满意的调度结果。

3 混合遗传算法的生产调度设计

根据上述思想，设计的混合遗传算法的基本步骤如下：

（1）输入数据，并初始化种群。

（2）计算种群的适配值的样本方差FSD.

（3）判断遗传算法的停止准则是否满足要求。如果满足停止算法，输出结果，否则继续以下步骤。

（4）基于当前种群进行选择交叉操作。

（5）计算种群的样本方差fsd,判断fsd是否小于FSD/n,若小于则进行第（6）步，如果大于则进行变异操作。

（6）初始化禁忌搜索算法，当前染色体即为初始解。

（7）判断禁忌搜索算法迭代准则是否满足要求，如果满足结束禁忌搜索，进行第（2）步；否则继续以下操作。

（8）产生候选解集。

（9）根据设定的渴望水平和禁忌表情况，选择一个解，并更新禁忌表。

（10）转到步骤（7）。

（11）转到步骤（2）。

4 仿真实验

本文的仿真试验中，以某机车车辆行业的10个零件、10台机器的调度问题为例。下面给出加工时间阵、机器顺序阵以及GATS算法计算10次所得的最优工件排序阵及其对应的最优加工Gantt图，如图1所示，最优解为87个单位时间。同时，该调度问题的Gantt图也明显地反映了此问题的求解复杂性。通过Gantt图可以清晰地了解到在每台机器上加工的工件及其各工序加工的起始时间和终止时间。如果调度的最佳解不是唯一的，则该调度算法同样也可以将它们全部搜索到，该算例的最佳调度结果就也不是唯一的，图1只是其中的一个最佳调度的Gantt图。

以下是其各个矩阵的表示方法，其中机器顺序阵为Jm;加工时间阵为T;工件排列阵为MJ.

（1）机器顺序阵Jm,Jm（i,j）表示加工i工件的第j个操作的机器号。

（2）加工时间阵T,T（i,j）为j工件在机器上的加工时间。

（3）工件排列阵MJ,MJ（i,j）为i机器上第j次加工的工件号。

实验在仿真环境下分别使用GATS和GA计算了10次，并且记录了每次得到目标函数的最小值，如表1所示。由表1的结果表明，禁忌搜索算法在10次运算中有2次达到最小值，而且最差的值与最优值之间的偏差也只有3,结果波动不大。

为了验证算法的有效性，在交叉算法和变异算法以及一些参数设置相同的情况下，采用传统的遗传算法重复运算10次得到的最优解为95,与最差值之间的偏差为8.同时可以比较出，禁忌搜索混合遗传算法比传统的遗传算法有较好的稳定性。

在充分分析机车车辆行业生产调度特点的基础上，提出的遗传算法和禁忌搜素算法混合的混合遗传算法应用在生产调度中。实验数据表明，改进的混合遗传算法既保存了遗传算法和禁忌搜索算法的各自优点，又针对各自的不足做了改进，使得混合遗传算法既克服了禁忌搜索算法对初始解的依赖性，又克服了遗传算法爬山能力差、易于早熟的缺点。实验证明，本文提出的混合遗传算法可以改善原有算法，是可行的。