引言

在超声波测距车载应用中，例如：超声波泊车辅助 （UPA） 和盲点探测 （BSD） 等，系统发射的超声波被周围物体反射回来。系统接收反射波（回波），然后将物体的回波振幅与某个阈值比较，从而实现探测物体的目的。物体越靠近系统，其回波也越强。因此，阈值随时间而变化，是一种相对常见的情况。本文将向您论述，该阈值无需变化，可以保持固定不变。

超声波测距

小轿车中使用的高级驾驶员辅助系统 （ADAS） 便是一种超声波测距应用。安装在车载前后保险杠和后视镜上的超声波传感器发射出超声波，然后接收周围物体反射回来的超声波。超声波的传播时间（飞行时间）用于计算到物体的距离，从而帮助驾驶员泊车：寻找泊车点，或者探测驾驶员盲点区域内的物体。车载前后保险杠安装的传感器达到 4 个之多，另外，每个后视镜上还各装有一个传感器。

在超声波高级驾驶员辅助系统中，压电式传感器一般用于将电信号转换为超声波，然后再把反射回来的超声波转换为电信号。接受反射回波时，压电式超声波传感器的低接收机灵敏度通常会导致电信号非常微弱。

图 1 显示了用于处理回波电压的典型信号链。TI PGA450-Q1 是一款集成车载超声波传感器信号调节器，适用于 UPA 系统等应用。

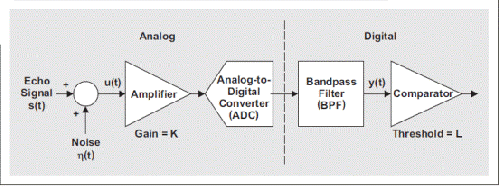
图 1 使用回波处理探测物体的 ADAS

超声波接收机接收到的回波信号s（t）被噪声破坏。图 1 所示输入相关噪声η（t）为外部环境噪声和所有信号链组成部分的和，其与时间（t）相关。被破坏的信号 u（t） 经由放大器使用增益 K 放大，然后通过一个模数转换器 （ADC） 被数字化。数字化的 AM 信号经过一个带通滤波器 （BPF） 按线路传输。该滤波器主要用于改善信号的信噪比。把经滤波后的信号 y（t） 与阈值 L 比较，以探测某个物体的存在。BPF 的后面一般会有一个振幅解调器，其将信号转换为基带，以进行比较。但是，本文为了方便说明，我们忽略了这种解调器。因此，探测物体的关键是阈值 （L） 的选择。那么，我们如何选择 L 呢？

回波振幅

发射器产生的超声波为一系列载波频率下的正弦波脉冲，并以声压级 （SPL） 来描述。SPL 的计算方法如下：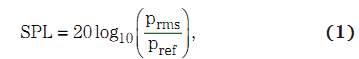

其中，Prms 为 RMS 声压，而 pref 为基准声压。常用基准声压为 20 Pa,即 0.0002 bar.

传感器对某个物体产生的超声波 SPL,取决于物体到传感器的距离。特别需要请注意的是，声压同距离成反比例关系：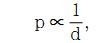

其中，p 为声波压力，而 d 为物体到传感器的距离。超声波传感器规范说明了30cm 距离的 SPL.由该值，利用这一距离定律，我们便可以计算出任意距离 x的 SPL:

其中，x 为传感器和物体之间的距离，并且 x > 30 cm.因此，x 距离的 SPL 为：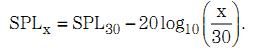

也就是说，超声波从传感器传播到物体过程中，会损失声压。

声波从物体反射回来，返回到传感器，声压进一步损失。另外，由于空气和物体都会吸收一部分声压，所接收回波的 SPL 可以通过方程式 3 进行近似计算。具体方程式请见本页末尾处，方程式中 α 为空气吸收系数。请注意，空气吸收的 SPL 与声波在空气中传播的距离与正比。换句话说，SPL 损失与 x 成正比。我们使用因数 2,是因为声波在传感器和物体之间传播两次-一次从传感器到物体，一次从物体到传感器。根据方程式 1,传感器接收的回波脉冲的声压计算方法如下：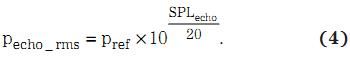

超声波接收机将接收到的声波转换为电信号。转换过程受到接收机灵敏度 （dB）的影响。1 Pa 声压产生 10 V 时，接收机灵敏度为 0 dB.因此，利用方程式 5和 6,可以把以 dB 表示的接收机灵敏度转换为 V/Pa.

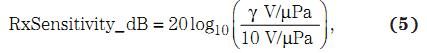
其中，γ 为以 V/Pa为单位的接收机灵敏度。方程式 5 可以重写为：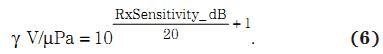

我们可以将方程式 4、5 和 6 组合为方程式 7（见本页末尾），以计算超声波接收机产生的电压。方程式 7 可以简写为：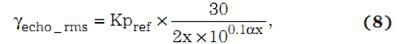

其中，增益（K）为一个常量。

方程式 8 表明，随着物体到传感器的距离 x 增加，回波电压下降。换句话说，物体越靠近，回波振幅变大，而物体远离时，回波振幅变小。

图 2 表明，接收到的电压与物体到传感器的距离有关，假设参数取值情况如下：

30cm 距离时发射 SPL= 106 dB

空气吸收=1.3 dB/m

物体吸收=0 dB

接收机灵敏度=–85 dB

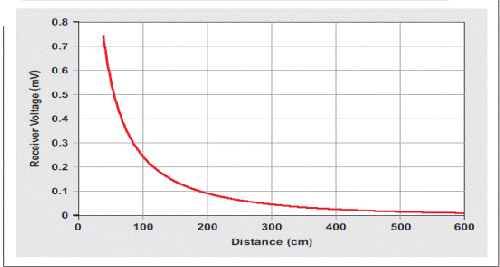
图 2 接收机电压为物体到传感器距离的函数

可变阈值方案

前一小节表明，从物体接收到的回波的振幅，会随物体到传感器的距离增加而减小。另外，由图1我们知道，回波处理路径的输入信号为u（t） = s（t） + η（t），其中s（t）为回波信号，而η（t）为输入相关噪声。换句话说，回波信号振幅不仅随距离增加而减小，并且会被噪声破坏，而回波处理系统只能通过处理回波信号来探测某个物体的存在。选择阈值时，一种常用的方法是阈值方案。使用这种方法时，阈值随时间而变化。特别是，超声波刚被发射出来时，阈值较大，之后，随着经过时间的增加而减小。这种方法的基本原理是，利用信号振幅的可预测衰变，确定阈值大小：越靠近物体，回波和阈值越大，从而实现物体探测。离物体越远，回波和阈值就越小。

图3描述了可变阈值方法的概念。该图显示了不同距离时物体回波解调举例。TI PGA450-Q1 评估模块的一个测试装置用于收集波形数据。该图显示了一种可能的阈值方案。

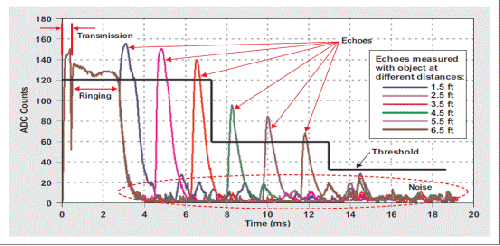
图 3 一个可能阈值方案的解调回波信号波形

尽管这种可变阈值方案方法原则上有效，但它存在两个缺点：

可变阈值方案要求器件内部有存储器，以将时间与阈值关系存储至方案表中。如果阈值有 3 个可能的取值（如图 3 所示），则该表就会有 6 种可能的输入。另外，对于车载中使用的高级驾驶员辅助系统 （ADAS） 来说，用户需要输入多种可能的传感器安装位置，因为传感器可以安装于车载保险杠或者后视镜上任何位置。例如，如果一个传感器有 10 个可能的安装位置，那么器件就需要存储多达 60 个位置数据。这就增加了器件的成本，因为要求使用更多的存储空间。

在车载保险杠和反视镜上安装好传感器后，系统制造厂商会“校准”方案表。校准过程就是确定各个阈值，以及切换阈值的时间。这种校准通常是一项耗时费钱的工作，特别是一个表中需要多个输入数据时更是这样。

总之，可变阈值方案的主要缺点是，它增加了超声波测距系统的总成本。

固定阈值

可变阈值方法使用基于时间变化的阈值，与这种方法不的同是，固定阈值方法将信号噪声用作基线。系统噪声用于确定阈值，这样物体不存在就不对其进行探测。

另外，由图 1 我们知道，回波处理路径输入信号为 u（t） = s（t） + η（t）。回波信号是一系列载波频率 fc（t） 下的正弦波脉冲，其计算方法如下：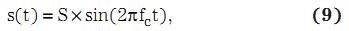

其中，S 为回波信号振幅。因此，方程式 10 给出了放大信号的 RMS 值：

请注意，这种一连串的脉冲仅短暂出现，从而让信号振幅看似受到长时间调制。

带通滤波器 （BPF） 的y （t） 输出可以表示为：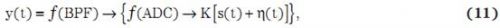

其中，（BPF） 为 BPF 的数字滤波器函数，而（ADC） 为 ADC 的量化函数。假设回波信号的基准时间为 t0 = 0（通常为发射器发射超声波的时间），则 y（t） < L、tend < t < tobject 和 y（tobject） ≥ L,并且 tend 大于零且为所发射脉冲初始脉冲群的末尾时，则可以声明 tobject 时探测到物体的存在。问题是，“我们可以选择使用一个固定阈值，弃用可变阈值方案吗？”要回答这个问题，我们可以利用方程式12,并假设t为一个瞬间值，从而照顾到各个噪声组成部分：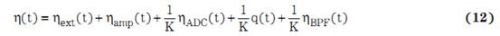

变量定义如下：

K=放大器增益

ηext（t）=外部噪声

ηamp（t）=放大器噪声

ηADC（t） = ADC电路噪声

q（t） = ADC量化

ηBPF（t） =BPF计算数学误差

各个噪声组成部分彼此不相关。另外，我们假设每个噪声组成部分为零平均值和非零方差高斯。

把方程式9和12代入方程式11后，BPF输出变为：

根据方程式9,BPF噪声的RMS为：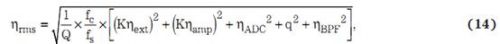

其中，Q 为 BPF 的品质因数，fs 为 ADC 采样频率，而所有噪声项均为 RMS值。知道方程式 14 所表示噪声的 RMS,并假设 6.6 波峰因数的情况下，所选阈值为：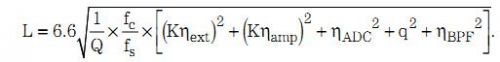

上述方程式可以表示为：

换句话说，我们可以利用方程式 15 选择固定阈值。图 4 显示了使用固定阈值的举例回波响应。

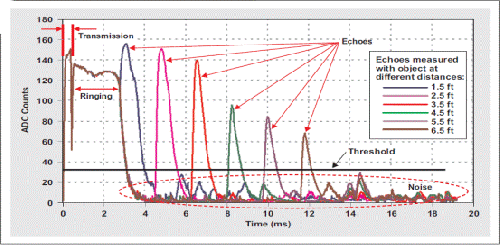
图 4 使用固定阈值处理回波数据

使用这种方法的一个明显优点是，它仅需要存储一个输入数据。如果一个传感器有 10 个可能的安装位置，只需总共存储 10 个输入数据便可。相比前面介绍的可变阈值方法，存储空间需求减少了 6 倍。请注意，如果放大器增益 （K） 改变，方程式 15 同样也提供了一种调节阈值的机制。

方程式 15 提供了一种确定阈值大小的分析方法。一般而言，需要利用噪声分析确定阈值大小。进行噪声分析的一种替代方法是，使用一个阈值对车载上安装的传感器进行校准。可将物体放置到传感器规定测距范围的最远处，然后完成测距校准。所选择的阈值需足够大，以在没有物体时超过处理后信号的噪声值，并确保仅在有物体时信号能够穿过该阈值。请注意，在使用这种方法选择阈值时，也应考虑 BPF 衰减。最后，为了提高物体探测系统的稳健性，信号的振幅必须在某段时间大于固定阈值。