1. 引言
强瞬态电磁脉冲辐射场能对电子系统产生较强的干扰及破坏,近年来愈来愈受到重视。对电磁脉冲能量的准确测量是研究瞬态电磁脉冲能量对电子设备的毁伤及其防护机理的基础工作。
瞬态电磁脉冲有以下特点:(1)脉冲的上升时间短(快的达亚纳秒量级,慢的为微秒量级); 宽度窄(窄的为纳秒量级,宽的为毫秒量级)。从频谱看,其能量分布在非常宽的频带上,可以从直流一直到几百兆赫兹。(2)我们关心的电磁脉冲辐射场多为近 区场,其电场与磁场之间不满足远场波阻抗关系,电场、磁场都要同时给出才能准确描述电磁脉冲场的特性。(3)电磁脉冲产生的随机性很强,重复性差。如雷电 电磁脉冲、舰船、飞机等电力电子系统的电磁脉冲辐射噪声时发生的时间、部位的随机性等。(4)测量空间有限,测试设备体积太大还会干扰被测场,影响测量的 精度。因此瞬态电磁脉冲辐射场的测量设备要满足以下几个要求:测量系统带宽满足测试要求;一次测量能同时得到三个极化方向的电场或磁场;测试设备体积小。
目前国内外普遍采用光纤传输系统来测量电磁脉冲辐射场。这些产品采用的传感器大多数都是单极化的,只能测量某一方向的电场或磁场。当需要了解同一场点的全部信息时,要分别沿不同极化方向对电场、磁场进行多次测试或者一次测量采用多个测量传感 器。这样的测量存在以下问题:(1)缺乏相位信息,不利于电场或磁场分量的合成;(2)而重复性较差的电磁脉冲采用多次测量的方法,不仅测量误差大,而且 有时难以实现;(3)一次测量采用多个测量传感器会引起相互的干扰,需要占用较大的空间,而且测量位置不能保证在同一点。
基于以上原因考虑,本文提出了一种三维瞬态电场测量天线模型-平板型结构,为了检验其效果,使用FDTD法对模型进行了数值模拟,得出了一些重要结论,对天线的实物设计提供依据。
2. 三维宽带天线的结构及其数据仿真
2.1 FDTD法
时域有限差分法(Finite Difference-Time Domain,简称FDTD是一种电磁场数值计算方法。该方法直接对依赖时间变量的Maxwell旋度方程做二阶精度的中心差分近似,把旋度方程 中电场和磁场的微分算子转换成差分形式,也就是说,它把Maxwell方程时间和空间上的连续变量在时域和空域中离散化,并在每个离散点上用差分代替微分。由于FDTD法直接来源于Maxwell方程,所以从理论上讲,它具有最广泛的适用性。
在对Maxwell方程差分化的过程中,FDTD存在着数值稳定性问题和数值色散问题。数值稳定性问题限制了时间步的大小:
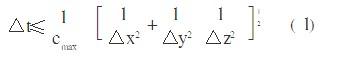
数值色散限制了一定频率下的网格尺寸,在计算时,通常要求 。其中,是被研究媒质空间的最小波长值(对应最高频率)。在模拟大结构时,有时将要求放宽为
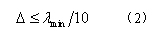 (2)
(2)
计算域的划分如图1所示,整个计算域是由六个面包围的立方体,四周设置10层的被修正的完 全匹配层 (MPML)吸收边界条件,为了便于入射波的引入和参数的提取,将整个计算区域分成两个区域:总场区和散射场区,它们的连接边界如图1 的虚线所示,入射波就从该边界引入。

2.2 三维传感器结构
对于数值模拟中传感器结构,选用平板型三维电场传感器,见图2。体积应尽可能的小以减少传感器对被测电场的影响,结构内部是10×10×10cm的导电立方体,作为天线的接地极;在它的六个表向外等距离放置大小相等的6个正方形导电平板,作为天线的极板。
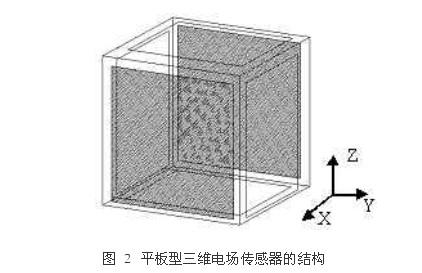
图2 平板型三维电场传感器的结构
为了使数值模拟的结果对传感器的实物设计提供依据,本文设计了5种模型,见表1,分两种情 况:第一组,保持正方形平板的尺寸不变,改变平板距离内部立方体的长度(No.1、2、3);第二组,保持平板距离内部立方体的长度不变,改变正方形平板 的尺寸大小(No.1、4、5)。
表1计算模型的机构
模型编号
天线极板边(cm)
天线极板到接地极的距离(nS)
1
8
1
2
8
0.5
3
8
1.5
4
6
1
5
4
1
HEMP的時域波形入圖3所示。其副值為5x100000V/m;上升前沿時間為2.47ns,脈沖寬度均為22ns。
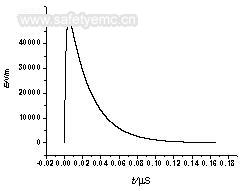
图3入射平面波电压波形
2.3 计算结果分析
FDTD计算中,空间步长取0. 5cm,时间步长取5×10-3/2c,c为自由空间的波速。计算区域60×60×60个空间步长,被10层的MPML包围。
(1)保持平板距离内部立方体的距离不变,改变正方形平板的边长。三个极化方向上天线的结 构对称,因此现只以Z方向上进行说明。Uz是Z方向上内部立方体与左右两边的正方形平行板之间的感应电压。当天线极板到接地极的距离均为1cm,改变天线 极板边长。当三维天线的z极化方向与入射波电场极化方向一致时计算结果见表2。图4是 Uz的典型波形,图5是HEMP与Uz的归一化波形对比,从图中可以看出,低频有失真。
表2第一组模型感应电压Uz的波形参数
模型号
天线极板边(cm)
峰值(V)
上升时间(nS)
脉宽(nS)
1
8
783
2.4
24
4
6
750
2.4
24
5
4
728
2.4
24
(2)保持正方形天线极板的边长不边,均为8cm,改变天线极板到内部接地体的距离,当三维天线的z极化方向与入射波电场极化方向一致时,Uz的计算结果见表3。
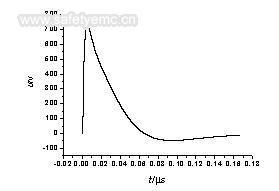
图4三维天线z方向感应电压z时的域波形
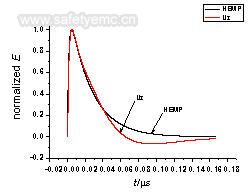
图5入射场波形与Uz归一化波形比较
表3第二组模型感应电压Uz的波形参数
模型号
距离长度(cm)
峰值(V)
上升时间(nS)
脉宽(nS)
1
1
783
2.4
24
2
0.5
399
2.4
24
3
1.5
1145
2.4
24
(3)为了研究改变导电立方体尺寸对三维测量带宽的影响,也设计一组计算模型,模型的结构参数及数值模拟的统计结果见表4。可以看出,接地极的边长的改变对天线的频率响应影响很大。
表4 仅改变接地体尺寸时的计算模型参数及天线频率响应数值仿真结果
序
号
计算模型参数
频率响应
接地极的边长(cm)
天线极板至接地极的距离(cm)
极板边长(cm)
感应电压的3dB带宽(MHz)
1
9
1.5
4
816
2
7
1.5
4
1010
3
6
1.5
4
1153
4
5
1.5
4
1376
5
4
1.5
4
1800
3. 结论
(1) 从数值模拟结果上来看,保持天线平板到内部立方体的距离不变,只改变正方形平板的尺寸大小,对感应电压影响不大;保持正方形平板的尺寸不变,改变平板到内部立方体的距离,对计算结果有很大影响,距离增加一倍,感应电压的峰值近似增加一倍。
(2)从感应电压的波形看,三维天线的高频响应很好,低频响应不足,需要在实际设计时对低频进行补偿。
(3)接地极的边长的改变对天线的频率响应影响很大,接地极的边长减小可以提高天线的带宽。
 畅学电子
畅学电子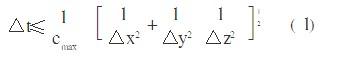
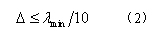 (2)
(2)