摘要：为了实现在不重新设计标准试飞数据处理软件的前提条件下，正确处理补码格式的试飞数据。通过分析试飞数据处理算法和校线的关系以及试飞数据和校线的关系，利用解析几何中线性方程横坐标平移不改变纵坐标数值的特性和补码格式数值的单调性，提出了仅对标准校线进行恰当地修改就能正确处理补码格式的试飞数据的一种方法。有效地保障了民机试飞任务的顺利进行，并为以后其他类型的试飞数据处理提供了解决思路。

关键词：补码；校线；传感器；数据处理

随着我国航空技术的不断发展，已经有实力自主研制民用飞机，以ARJ21为代表的支线客机以闪亮登上国际客机序列的历史舞台，即将在国际支线客机领域里占上一席之地。支线客机包含复杂的电子系统，被测试的参数多达上万，所以会产生多种格式的试飞数据。

飞行试验数据是支线飞机研制过程飞行试验中所获得的最宝贵的科研信息资料，凝聚了设计、制造、试飞等多方面技术人员的心血，甚至冒着生命危险而取得。飞行试验数据数据处理是飞行试验工程中非常重要的环节，直接提供了试飞数据结果。该结果不仅为支线飞机的试验定型、鉴定、合格审定等提供最直接的定量依据，同时也是被试对象全面、客观真实的模型的数字体现。

试飞数据处理结果是数据处理工程师对飞行试验原始数据进行校准、解算的结果。试飞工程师通过分析数据处理结果，得出被试飞机的性能指标是否满足设计要求、存在哪些不足、以及如何改进等结论，为飞机定型和改良提供重要的科学依据。试飞数据处理结果的准确性直接影响试飞定型的结果。

1 补码的概念和性质

1．1 补码的概念

数值在计算机中表示的形式为机器数，计算机只能识别0和1，使用的是二进制，为了能方便与二进制的转换，还使用了十六进制和八进制。下面将介绍为何要引入补码这个概念。

数值有正负之分，计算机就是用一个数的最高位存放符号(0为正，1为负)来区分正负数的，这就是机器数的原码。假设机器能处理的位数为8，即字长为1 b，原码能表示数值的范围为-127～0，+0～127共256个。

有了数值的表示方法就可以对数进行算术运算，但是很快就发现用带符号位的原码进行乘除运算时结果正确，而在加减运算的时候就出现了问题，如([x]表示十进制x，假设字长为8 b)：[1]-[1]=[1]+([-1])=[0]，但(00000001)原+(10000001)原=(10000010)原=[-2]，显然不正确。因为在两个整数的加法运算中是没有问题的，于是就发现问题出现在带符号位的负数身上。为了解决这个问题，又引入了反码。对除符号位外的其余各位逐位取反就产生了反码。反码的取值空间和原码相同且一一对应。下面是反码的减法运算：[1]-[2]=[1]+[-2]=[-1]，(00000001)反+(11111101)反=(11111110)反=[1]，正确。[1]-[1]=[1]+[-1]=[0]，但(00000001)反+(11111110)反=(11111111)反=[-0]有问题。事实上，上面的计算出现了+0和-0，在人们的计算概念中零是没有正负之分的，于是就引入了补码这个概念。负数的补码就是对反码加一，而正数的原码、反码、补码是一样的。在补码中用-128代替了-0，所以补码的表示范围为：-128～0～127共256个。注意：-128没有相对应的原码和反码，[-128]=(10000000)。补码设计的目的是：第一，使符号位能与有效值部分一起参加运算，从而简化运算规则。第二，使减法运算转换为加法运算，进一步简化计算机中运算器的线路设计。经过上面的讨论，可以得出任意进制数的补码的表示形式：设R为基数，位数为n的原码N，补码为：(N)补=Rn-N。以十进制为例，2的补码为：(2)补=10-2=8，46的补码为：(46)补=100-46=54。

1．2 补码的性质

1．2．1 取值范围

设基数为2，位数为n：

(1)原码的表示范围：-(2n-1-1)～+(2n-1-1)

(2)反码的表示范围：-(2n-1-1)～+(2n-1-1)

(3)补码的表示范围：-2n-1～+(2n-1-1)

1．2．2 加减运算的性质

(1)一个正数的补码执行求补运算，其结果恰是与其绝对值相同的负数的补码；同样地，对一个负数的补码执行求补运算，其结果恰是与其绝对值相同的正数的补码。可用公式表示：(+x)补求补←→(-x)补求补。

(2)两个数补码的和，等于这两个数和的补码。可用公式表示：(x)补+(y)补=(x+y)补。

(3)两个数补码的差，等于这两个数差的补码。可用公式表示：(x)补-(y)补=(x-y)补。

1．2．3 单调性

把二进制补码的符号位转化成数值位，如果二进制数值对应的十进制数值越大，则实际表示的负数值越大，反之，亦然。例如：[-1]补=(1111 1111 1111 1111)=[655 35]，[-2]补=(1111 1111 1111 1110)=[655 34]。

2 试飞数据处理算法分析

2．1 校线的概念以及校线和传感器的关系

校线是校准曲线的简称，指在规定条件下，表示被测量值与仪器仪表实际测得值之间关系的曲线。它主要包括直线校准、抛物线校准，多项式校准和双曲线校准等。

在支线飞机试飞中，有一部分测试参数属于加装参数，通过各种类型的传感器配合测试技术才能完成对这些参数的测量工作。下面简要介绍传感器的概念和工作原理。

传感器是一种能把物理量或化学量转变成便于利用的电信号的器件。传感器把某种形式的能量转换成另一种形式的能量。它有有源的和无源的两类：有源传感器能将一种能量形式直接转变成另一种，不需要外接的能源或激励源。无源传感器不能直接转换能量形式，但它能控制从另一输入端输入的能量或激励能，传感器承担将某个对象或过程的特定特性转换成数量的工作。其“对象”可以是固体、液体或气体，而它们的状态可以是静态的，也可以是动态(即过程)的。对象特性被转换量化后可以通过多种方式检测。对象的特性可以是物理性质的，也可以是化学性质的。按照其工作原理，它将对象特性或状态参数转换成可测定的电学量，然后将此电信号分离出来，送入传感器系统加以评测或标示。

从传感器的工作原理可知，传感器把物理量转化成电信号输出，电信号通常用电压表示，而电压值在采集时被转换成码值(16位的整型值)，所以，电信号和物理量的对应关系将转换成码值和物理量的对应关系。在试飞数据处理中，码值和物理量对应关系的点的对数又被叫做点对校准曲线。

2．2 校线在试飞数据处理算法中的作用

从第2．1节的介绍中看出，校线实际上就是测试记录的试飞数据原码到实际工程中物理量的对应关系。理论上，点对校准曲线的点对个数越多，数据处理的结果越准确。然而，在实际工程应用中，不能枚举所有点对关系，仅选择有代表性的几个点对关系。那么如何解算未在校线中出现的原码的物理量。在试飞数据处理技术中已经形成了非常成熟的算法——线性插值方法。根据实际需要，采用线性内插和线性外插相结合的方式完成所有试飞数据原码到物理量的解算任务。通常情况下，原码值被当做16位无符号整型数值进行处理。

为了方便说明点对校准曲线和试飞数据算法是如何有机结合，完成试飞数据处理的，引入了二维直角坐标系和直线方程进行详细分析讨论。对于直线，可以用数学方程的形式表示为：y=kx+b。当k≠0时，直线可以表示为：y=k(x+b／k)，当k=0时，直线可以表示为：y=b。在试飞数据处理中，k=0是没有意义的，所以讨论的所有问题的表现形式均是y=kx。对于点对校准的应用可以用图1，图2来说明(其中图1和图2中实心点的x坐标，从左到右的依次为x1，x2，x3，x4，x5，对应y坐标为y1，y2，y3，y4，y5)。

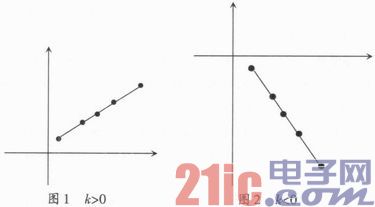
图中的实心点就是点对校准曲线的特征点。标准化的试飞数据处理软件对于特征点内的原码值采用线性内插值解算对应的物理量，对于特征点外的原码值采用线性外插值解算对应的物理量。从实际工程应用中可知，校线的特征点连线并不是一条直线，而是一条折线段，所以，选取校线的特征点越多，数据结果的精度越高。

3 补码格式数据处理方法的研究

当特殊类型的测试参数的原码被记录成补码格式，并按照图3给出相应的校线。

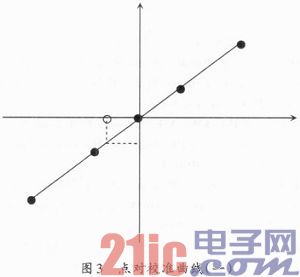
图3中的虚心点表示要求解的参数对应的码值，通过线性内插值，很容易求出参数在这一点的对应的物理量。但是，如果不考虑补码情况下，原码值将被认为是超过32 767的正整数值，如图4所示。

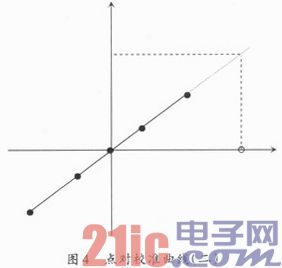
按照线性外插值求解，结果显然是错误(其中，除了原点，图3和图4实心点的x坐标，从左到右的依次为x1，x2，x3，x4，对应)y坐标为y1，y2，y3，y4。虚心点坐标(x，y)。以后图例中坐标点均按此规定描述)。

通过线性方程进行分析，修改点对校准曲线，可以解决这个问题。修改点对校准曲线的方法是，将码值为非负整数的特征点保持不便，把码值为负整数的特征点换算成补码，然后将补码按照无符号值和原码值对应，构成新的点对校准曲线，按照补码的单调性和直线的平移性可知，这种方式的变换不改变计算的结果。

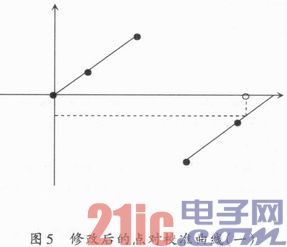
转换后的点对校准曲线如图5所示，按照这种方式就能求解出正确的物理量。但是，还有一种特殊情况没有考虑到，如果仅仅按照转化点对校准曲线的方法来处理补码数据，对于大于x2又小于32 767的值，将会出现错误，如图6所示。

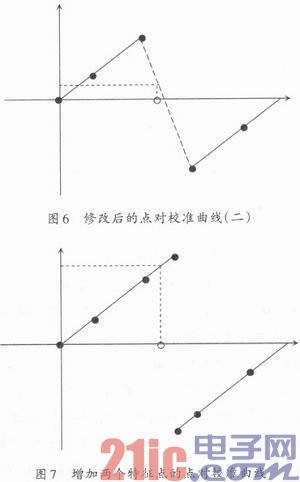
从图6中可以看出，对于大于x2小于x3的码值，经过上述方法进行处理，将得到错误的物理量。通过增加点对校准曲线的特征点可以解决这种特殊情况。在特征点x2和x3之间加入两个新的特征点x2’=32 767和x3’=32 768，并按照线性外插分别求出x2’对应的物理量y2’和x3’对应的物理量y3’，如图7所示。

由图7可知，能正确解算图6出现的特殊情况。

4 结语

本文通过讨论校准曲线和试飞数据处理方法的关系，以及补码在数值上单调性，采用解析几何中线性方程平移的特性。提出了仅对校准曲线做一定的修改，就能正确处理补码格式的试飞数据。这种解决方法不用修改标准化的试飞数据处理软件，就能得到正确的试飞数据处理结果，有效地保障了支线飞机定型试飞任务的顺利进行。同时，也给生成校准曲线的试飞工程师提供了一种解决类似问题的思路。