本文先通过电磁环境、抛物方程的预测方法，推导出抛物方程计算总的传播损耗等于传播因子和损耗因子对 电磁波场量的叠加，设计了电磁环境预测系统。最后以海战场电磁环境为例进行了仿真，结果证明该方法对陆海空等典型地海场景中的复杂电磁环境电磁波场强或接 收功率的预测是非常有效的，具有较好的理论研究和应用价值。

0 引言

雷达、远距离无线通信、北斗卫星导航系统（BDS）、电子对抗还是遥感遥测等依赖电磁波的系统，都避免不了对电磁波传播特性的分析。对复杂环境中的电磁波传播一种粗略的分析方法是将环境视为自由空间，而精确的分析 必然考虑电波传播实际环境如地形、地物以及大气层环境变化的影响等。然而传统解析法如基尔霍夫近似法（Kirchhoff Approximation,KA）、微扰法（SmallPerturbation Method,SPM）等不能用于求解粗糙表面的散射特性，虽然最近发展了一些改进算法，但未考虑大气环境的影响，且计算量较大。射线追踪法可以定量地描 述电磁波在各种大气环境条件下的轨迹，但没有解决场分布的问题。抛物方程法可处理非均匀大气与复杂边界条件下的电磁波传播问题，且可用迭代法求解，在解决电磁波传播问题方面得到了广泛运用。

由于电磁环境构成较为复杂，本文只研究构成电磁环境中最主要部分，它是影响处于电磁环境中武器平台的关键因素，主要包括自然界热噪声和人为产生的无线电发射。自然界热噪声一般为高斯白噪声，它均匀地分布在每个频率上，主要影响无线电接收机的底噪电平，决定了无线电接收机的接收灵敏度或者说是通信质量。人为产生的无线电发射往往会对不同地区产生不同影响。因此刻画电磁环境应采用场论的方法，主要采用的物理量为场强。根据电磁波传播路径损耗、天线方向增益、发射功率，就可以预测某个地理位置的最大场强的大小。综合多个发射电台在某一地理位置场强的大小和热噪声就可以描述某个地理位置的电磁环境。

由于军用复杂电磁环境的构成以30 MHz~300 GHz为主，因此本文仅研究该频段内复杂电磁环境的预测方法。

1 基于统计模型的复杂电磁环境预测方法

复杂电磁环境主要由自然电磁辐射和人为电磁辐射形成。自然电磁辐射主要是热噪声，人为电磁辐射主要 是无线电发射电台。这两者是形成复杂电磁环境的关键因素。此外，不同地域电磁环境不同，或者说是电磁环境与地理位置有关，因此描述和刻画电磁环境应采用物 理学中场论的方法。也就是说描述电磁环境的最佳物理量是场强或功率通量密度。场强是矢量，功率通量密度是标量。这两个物理量之间可以相互转换。

1.1 人为电磁辐射对电磁环境的影响

对于主要影响电磁环境之一的无线电发射电台，它影响电磁环境的主要发射参数模型如图1所示，主要包括了工作频段内的必要带宽内发射、带外发射、杂散、谐波。因此，在构造电磁环境时这些因素都应当考虑在内。

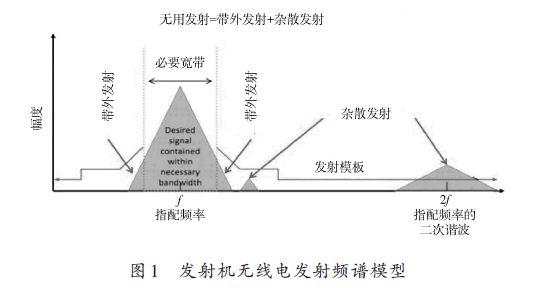
必要带宽内发射一般称为带内发射，带外发射和杂散发射一般称为无用发射。带内发射和无用发射的大小主要由发射功率和滤波器决 定。由于各个生产厂家在生产设备时选择的滤波器不同，因地不同厂家生产的无线电设备造成的无用发射也不一样。但是凡是经过型号核准或无线电发射机检测的无 线电设备都必须满足规定的发射模板（或频谱模板）的技术指标规范。表1给出了我国8 MHz数字电视地面广播传输系统的发射模板。因此，可以根据发射模板预测发射设备的最大无用发射功率。这一方法也满足电磁干扰预测的保守原则。

为了预测的准确度，必须考虑特殊区域的地理地形条件和定向接收天线的方位。电磁波即使在自由空间的传播，定向天线接收到的信号强度也与天线的方向有关，因而收到的信号强度不同。下面举例进行说明。

假设在同样的电磁环境中，完全相同的两个接收天线的地理位置和接收天线方向如图2所示。由于辐射源和被干扰设备的相对位置与方位不同，从而对被干扰设备的干扰程度不同，而且干扰程度与夹角θ 有关。

对于图2中所示的地理位置关系，目前研究的方法有3种：以水平面为基准，将被干扰设备等效到水平平面；以被干扰设备为基准，将辐射源等效到高度为h 的水平面；以辐射源与高度为h 的被干扰设备之间的连接虚线所在平面为基准，将辐射源和被干扰设备等效到该平面上。

1.2 自然电磁辐射对电磁环境的影响

自然电磁辐射最重要的就是热噪声。热噪声是稳定上升到绝对零度（开氏温标K,0 K=-273 ℃）以上时激发的电子随机运动引起的。它可以像其他电磁能量那样产生辐射，特性是高斯白噪声，分布在每个频率上。噪声功率表达式为：

工程应用中，为分辨小信号一般采用式（1）的对数并乘以10的形式，于是得到噪声功率为：

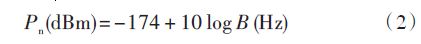
1.3 无线电磁波的传播

无线电磁波在传播过程中主要遭受到的损耗是扩散损耗、路径损耗和吸收损耗。扩散损耗主要是无线电磁 波的球面效应（惠更斯原理）产生的损耗。路径损耗是无线电磁波在传播中遇到障碍物时产生的损耗。吸收损耗主要是无线电磁波受到大气中水和氧气引起的损耗。 由于高频才出现吸收损耗，一般来说不考虑电磁波的吸收损耗。对于自由空间来说，电磁波因扩散（见图3）形成的自由空间损耗为：

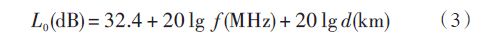
电磁波的自由空间损耗与电磁波传播的频率和距离密切相关。它决定了无线电发射台站对某一地理位置的最大场强的预测，影响到无线电台站间部署的位置、使用的频率和发射的功率等参数。最大场强预测公式为：

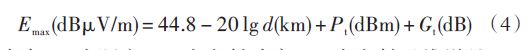
比较典型的有Egli模型，Okumura-Hata模型，CCIR（ITU-R）公式，Ibrahim-Parsons 模型，COST 231-Hata 模型，Lee模型等。

在构成复杂电磁环境的多个无线电的第i 个辐射源，它在某一位置j 产生的最大场强为：

这样遍历所考虑的辐射源集合的每个元素，即i ={1,2,3,…，N} 就可以知道各辐射源对某一个地理位置电磁环境构成的影响。

2 基于PE的复杂电磁环境预测方法

抛物型方程（Parabolic Equation,PE）是从基本的麦克斯韦方程组经严格推导，分离掉时间因子和后向传播分量后得来的，并且方程中包含了折射效应和绕射效应，满足全波解 的要求，通过PE 方程能够很好地解决直、绕射和散射等过程对电磁波传播的影响，从而给出电磁场强预测的确定解。

在线性、各向同性的均匀媒质中，E 和H 满足的麦克斯韦方程的微分形式如下：

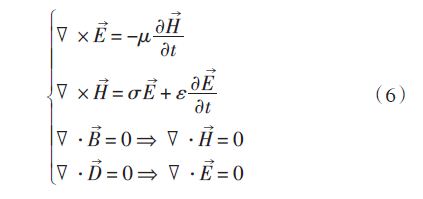
上述方程组中，μ 是磁导率，ε是电容率，σ 是电导率。

根据取旋度与求导法则得：

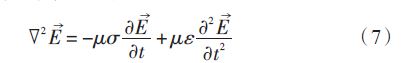
式（7）称为电场的一般波动方程。

研究二维坐标下的电磁波传播特性。即为在x-z直角坐标系内建立电磁波传播模型，其中x 代表水平传播方向，z 代表垂直传播方向，如图4所示。

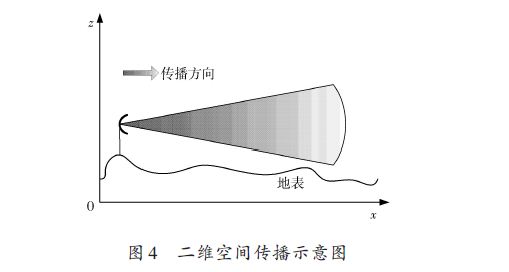
当计算区域选择在二维坐标系中时，引入时谐矢量场Ψ ,其表达式为：

则得到了二维坐标系情况下的标准抛物型方程（SPE）表达式。

场强的大小或分布取决于在传播路径上的损耗情况。求解SPE解时可将场量进行分解，分解后的结果为两个不同因子的乘积。因此，传播损耗在数值上等于传播空间的传播损耗（称为损耗因子）与电磁波发射天线的空间发散损耗（称为传播因子）之和。

传播空间的传播损耗不仅与电磁波的波长或频率有关，还与传播距离的大小有关，单位为dBW,其表达式如下：

电磁波发散损耗的大小，等于参考点处电场值与自由空间中全向天线在同一点处电场值的比值，根据本文中u 的表达式，则发散损耗为：

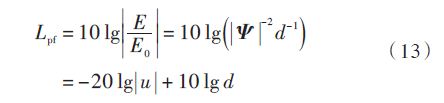
式中：d 为参考点与天线之间的水平距离，单位为km;λ 为波长，单位为m.

在传输平面内，总的传播损耗等于传播因子和损耗因子对电磁波场量的叠加，从而基于SPE的传播模型其总的传播损耗为：

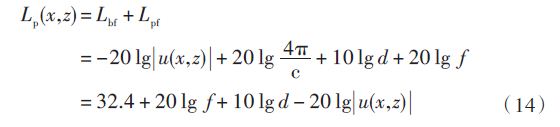
其中电磁波频率的单位为MHz.利用PE方程确定了无线电磁波的传播损耗，即可计算接收点的接收功率，确定该点的电磁环境。

3 复杂电磁环境预测系统

基于以上理论分析，构建典型场景下的电磁环境预测系统。复杂电磁环境预测系统由四个模块组成，即参数输入模块，图形显示模块，操作模块和结果显示模块。其中，参数输入模块包括典型战场场景选择，辐射源及接收点参数设置，地图加载等。复杂电磁环境预测系统演示总界面如图5所示。

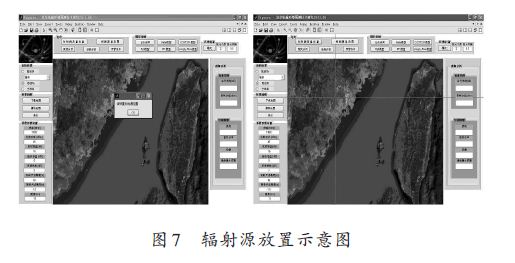
场景分为三种，如图6所示。操作模块包括辐射源放置，场强预测，图形绘制，模型选择，可以根据战场 环境特点，选择相应模型进行图形绘制与分析。以海战场为例进行复杂电磁环境预测，并给出分析结果。辐射源放置如图7所示，仿真参数设置如下：辐射源频率1 500 MHz,发射功率46 dBm,发射增益16 dB,接收增益为0 dB,系统损耗为3 dB,发射天线高度为30 m,接收天线高度为1.5 m,收发天线距离为15 km .

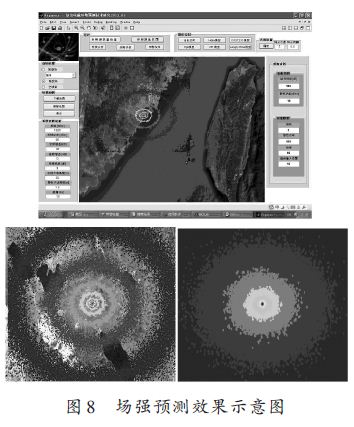
距辐射源一定距离的接收点处的电磁环境预测结果如图8所示，覆盖区的接收功率用颜色的深浅（由红至蓝）来衡量，其中红色表示功率越强，蓝色表示越弱。

如图9 所示分别给出了自由空间、基于统计模型（Oku-mura-Hata）以及基于PE 的电磁波传播损耗、接收功率及场强随距离的变化关系。

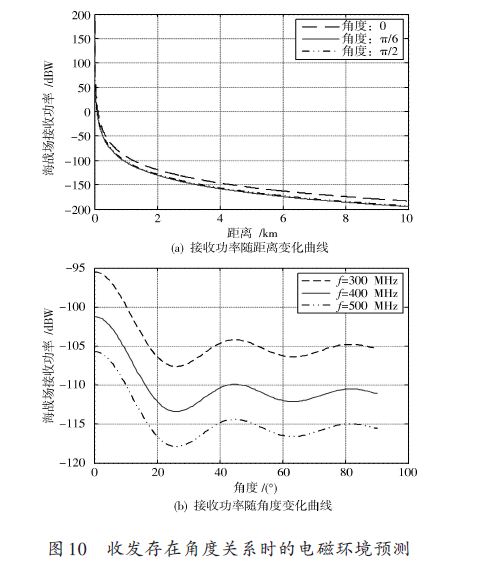
当辐射源与定向接收存在角度关系时，不同工作频率及角度关系下，接收点的功率如图10 所示。图10（a）为不同角度接收功率随距离的变化；图10（b）为不同频率接收功率随角度的变化。

当海面电磁波传播收发天线高度均为10 m,海面路径0.6倍菲涅耳间隔路径距离内没有障碍，计算模型与ITU-R_P.1546-3模型的仿真对比如图11所示。

对特定战场环境中某地理位置处的电磁环境进行预测，即可按照上述思路，在考虑影响辐射源电磁辐射因素的基础上，结合具体的环境信息，在不同环境场景中调用不同的电磁波传播模型，最终实现电磁环境的预测。

4 结语

从以上的仿真可以看出，本系统可以方便、快速地模拟计算出电磁波在复杂战场环境下的路径损耗、接收功率与场强值，并能够直观、实时地显示，因此，复杂电磁环境预测系统对于战场复杂电磁环境下武器装备受扰分析与效能评估具有辅助作用。本仿真系统在电磁环 境预测过程中，虽然考虑了电磁波传播路径损耗、天线方向增益、发射功率等因素，但对于传播路径损耗影响因素、天线极化特性等，考虑得还不是很充分，因此本 系统还有待于完善，将以上因素考虑进去，将为今后的电磁环境预测系统提供更加完美的仿真环境。