实际应用经常只会用到数据转换器模拟信号范围的一部分。如果在应用中只用到该范围的一半或者四分之一，则可以很容易地计算出有效分辨率。但如果遇到的是一个更复杂的分数，又该怎么办呢？本文将介绍在使用任何模拟信号范围时有效分辨率的计算。

电压裕量

模拟系统通常会留出一定的裕量，以针对增益误差、漂移、设计容限或设备调校不佳进行调整。在模拟世界和数字世界之间进行转换时，我们同样需要在数字世界保留一定的裕量。以0至10V的工业控制电压为例，如果我们只允许ADC量化最大10V的电压，那么，所有的下行设备必须限制在10V，否则将会丢失信息。因此，工业控制中通常留有5%甚至20%的裕量。

其他系统（例如视频系统）往往在视频信号中添加了同步信号。1VP-P视频信号中很可能包括700mV的有用视频信号和300mV的同步脉冲。如果利用12位ADC对这样的信号进行数字转换，视频本身将仅使用可用范围的70%，或者4096个可用代码中只使用2867个代码。现在，如果保留5%的裕量，则使用范围将会更低。

因此，在模拟和数字世界之间转换时，我们必须保证数字世界能够应对系统裕量。这一点很重要，但应对裕量却造成了有效分辨率的降低。

任意模拟范围的有效分辨率计算

我们首先从小孩的数学练习开始——真有这么简单吗？

我儿子最近问了我一道数学题，大致内容如下。我有一张巨大的纸，将其剪成两半；我将这两半摞在一起，那么总厚度将为原来的2倍。现在，我又将这叠纸剪成两半，并再次将它们摞在一起。此时的总厚度为最初单张纸的4倍。依此类推，重复以上过程多少次后，纸摞起来的高度可以到达月亮？

他需要推导的公式与计算有效分辨率的公式非常相似，公式中使用了对数。

以电压为0至10V、20%裕量的工业控制为例，实际范围为0至12V。如果采用16位DAC，那么0至10V信号的有效分辨率是多少（图1）？

图1：理想的16位DAC特性，为系统设计留有容限和裕量。

我们知道，对于R位分辨率的DAC，其阶梯数量为2R。因此，定义N为阶梯数量：

我们需要求出R，所以需要用到对数计算。在等式两侧取对数：

式子简化为：

回到工业控制的例子，对于0至10V的范围，实际上仅使用了可用阶梯数量的10/12=0.833倍。在一个16位的系统中，编码值为54613。将该数字代入公式，即可计算出有效分辨率：

因此，如果留出20%裕量，有效分辨率仅降低了大约0.3位。

实际上，就位数而言，减少的位数与原始分辨率无关。我们可以通过所用代码与可用代码之比得出减少的位数。

因此，在以上700mV视频和300mV同步信号的视频例子中，使用了0.7倍的可用代码：

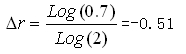
结果损失了0.51位。所以，在12位系统中的有效分辨率为11.49位，在16位系统中为15.49位。

对于那些想知道剪多少次纸后才能从地球到达月球的人，可以进行以下计算：纸堆的高度T=p×2C，式中：p为单张纸的厚度，C为剪纸的次数。注意到相似性了吗？按照相同的方式，我们可求解出C，于是C=Log（T/p）/Log（2）。

如何完成我儿子的家庭作业呢？我测得一张打印纸的厚度为0.11mm。月球与地球的距离大约为300，000km。因此，我们需要剪纸的次数为Log（3×1011/0.11）/Log（2）=42次。好，我们现在动手……所需的时间并不长嘛。所需剪纸的次数少得让人难以置信。

本文小结

在任何进行模拟和数字世界相互转换的系统中，我们都要考虑裕量。这通常会降低系统的有效分辨率。本文推导的公式能够在已知模拟信号占数字范围比例的条件下，计算出有效分辨率。实际上，正如示例所示，即使留出较大的裕量开销，所减少的ENOB也不到1位。