0 引言
出于实现成本和复杂度考虑,数字通信接收机通常采用固定频率晶振实现信号采样。由于工艺原因,实际频率和额定频率之间会存在不可避免的频率误差,从而使得基于数字电路实现的采样钟恢复环路是多数系统中的必不可少的模块之一。
目前,针对不同场景,学者们已经提出了多种采样钟恢复算法[1?3],它们的基本架构类似,主要区别在于定时误差检测采用的算法不同,而且对输入信号的特性要求也不同。纵观这些定时误差检测算法,最常用的包括Gardner检测算法[4?5]和相关检测算法[2].其中,前者要求输入检测器的数据率为符号率的两倍,而且数据中的过零点要足够多,目前,这种方法已经成功应用到欧洲DVB?C、美国ATSC?T等多种系统接收机实现中。另外,由于卫星通信中多采用低阶QPSK等调制方式,满足其对过零特性的要求,Gardner算法在卫星通信领域也有很大的应用前景,如DVB?S/DVB?S2等系统接收机。相关检测算法适合发送信号中包含一段已知的训练信号,且该段数据的自相关特性较优,算法需要输入的数据率是符号率的四倍,相关检测算法也有很广泛的应用,也涌现了许多改进算法以及在基本构架基础上的并行实现方法[6?11].
但是,实际的通信体制中,存在许多场景,仅部分信号满足过零特性,如仅有一段数据采用过零特性较好的调制方式,其他数据采用OFDM 调制或者其他调制方式。此时,上文提到的两种检测方法都不能直接应用。
出于这种考虑,本文给出了一种结合使能控制的采样钟同步实现方法,该方法既利用了通常的Gardner算法结构,具有低复杂度特性,又保证了环路可以可靠工作。
1 典型的基于Gardner 算法的采样钟同步环路
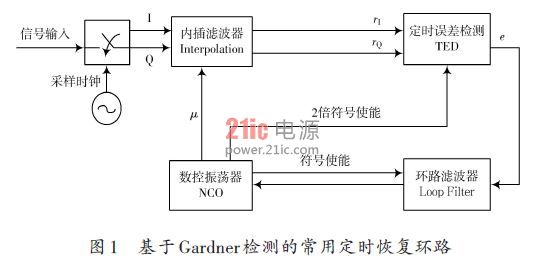
如图1 所示,基于Gardner 算法的采样钟同步环路包括四个主要部分:内插滤波器、Gardner定时误差检测器、低通滤波器和数控振荡器。内插滤波器根据输入的数据序列和小数因子内插得到新的数据符号,可以采用三角内插、分段抛物内插等实现,其内插性能决定了环路的恢复精度;低通滤波器实现对估计误差的滤波,其带宽决定了环路是否收敛、收敛速度以及收敛精度;数控振荡器根据滤波器输出计算符号率使能信号和两倍的符号率使能信号,其中前者控制滤波器,后者控制Gardner 定时误差检测器。Gardner 定时误差检测器用三个连续的采样点来求得定时误差,即:

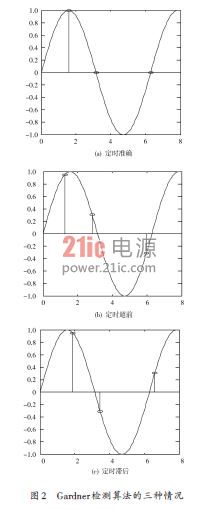
式中:r(1/ 2 - τ) ,r(-τ) ,r(1 - τ) 分别表示中间时刻、前一时刻以及后一时刻对应的采样点,三个采样点的示意如图2所示:
2 结合使能控制的采样钟同步实现方法
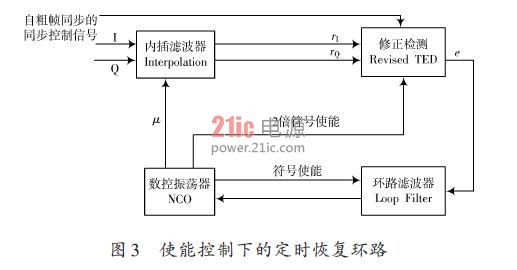
接收机首先通过相关等得到粗同步信号,用于指示满足过零点特性的数据段,其次采样钟恢复环路通过输入的粗同步信号控制整个环路工作,如图3所示。
环路工作流程如下:
(1)采样数据送入内插滤波器后,根据小数因子计算内插后符号;
(2)内插符号作为定时误差检测器的输入,如果粗同步使能信号为高,内插后的符号数据用于计算定时误差,两倍符号使能信号为高时检测器工作;
否则,定时误差设置为零;
(3)定时误差结果送入低通滤波器,符号使能为高时滤波器工作;
(4)低通滤波器输出给数控振荡器;
(5)数控振荡器生成符号使能信号控制低通滤波器,生成两倍符号使能信号控制定时误差检测器,从而形成一个闭环。
3 计算机仿真分析
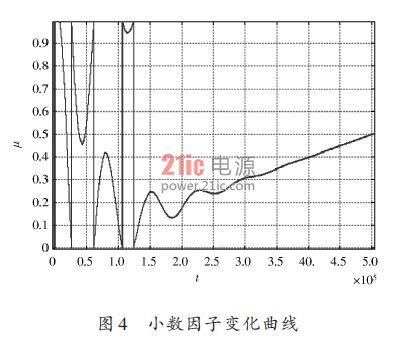
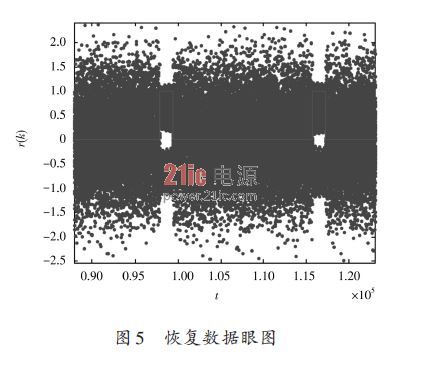
图4和图5分别给出了仅有10%可同步信号时的小数因子μ变化曲线以及恢复的数据眼图,其中可同步部分采用QPSK,其他部分未任意调制数据。如果输入数据总满足过零特性,此时恢复信号性能最佳,和全工作环路相比较而言,使能控制环路会出现误差增加现象,但是,如果信道PPM足够小,该方案恢复精度完全满足需求。
4 结论
本文通过利用同步控制信号,提出了一种改进的定时恢复算法实现结构,并给出了具体的实现流程,通过仿真说明了算法的可行性。提出实现结构可用于任何发送信号为部分信号满足多零点要求的场景,具有较高的工程实现价值,目前已经成功应用到伪随机(PN)+正交频分复用(OFDM)体制的解调器中。