心电信号检测是医生诊断治疗心血管疾病的重要辅助手段，但由于心电信号检测实际条件不理想，心电信号中常混有各种干扰信号，常见有肌电干扰、基线漂移和工频干扰。文中针对肌电干扰，采用数字滤波方法进行了去除噪声的滤波器设计。并通过对心电图信号滤波器的设计，不仅提高了ECG信号滤波器的去噪效果，且提高了工作效率。

现代医学表明，心电信号（Electrocardiograph，ECG）含有临床诊断心血管疾病的大量信息，心电信号的检测是心血管疾病预防诊断的重要辅助手段。而实际中心电信号中通常混入各种随机噪声。噪声的存在降低了诊断的准确性。因此，如何有效去除各种干扰和噪声是务必要解决的问题。

国际上最先用于完成心电信号滤波任务的是通过不同的电子元器件组成模拟电路来实现滤波功能的模拟心电滤波器。但这种模拟心电滤波器需较为复杂的电路，滤波效果也不理想，且成本较高，因而未得到大规模应用。目前数字滤波器由于性能可靠、精度高、设计简单等优点已被广泛采用，尤其是应用计算机软件编程的方法已成为国际上心电图机滤波干扰的主要手段。

1肌电干扰及常用数字滤波方法

1.1心电信号中的肌电干扰

心电信号检测主要存在肌电干扰、基线漂移和工频干扰3种噪声。而其中影响较大的则是肌电干扰。所谓肌电干扰，指人体多种电现象混杂在一起，某一生理量有时是信号，在另一场合则可能是噪声，即被测生理变量以外的人体电现象所引起的噪声。肌电干扰由人体肌肉颤动引起，发生率具有随机性，频率范围在5～2 000 Hz之间。

1.2常用的数字滤波方法介绍

（1）切比雪夫数字低通滤波器。其在过渡带比巴特沃斯数字低通滤波器的衰减快，对噪声的去除效果较好，但频率响应的幅频特性不如巴特沃斯数字低通滤波器平坦，在通频带内存在幅度波动。而切比雪夫数字低通滤波器和理想滤波器的频率响应曲线之间的误差最小。

（2）巴特沃斯带阻滤波器。是在通带内有最大平坦的频率响应曲线，能最大限度地让通带内的信号通过，在阻带则逐渐地下降为零。在振幅的对数对角频率波特图上，从某一边界角频率开始，振幅随角频率的增加逐步减少，趋向负无穷。

（3）小波变换算法。是一种新的变换分析方法，其继承和发展了短时傅里叶变换局部化的思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的时间——频率窗口，是进行信号时频分析和处理的理想工具。其主要特点是通过变换能够充分突出问题某些方面的特征，因此，小波变换在许多领域均得到了成功的应用。

（4）双线性Z变换法设计数字滤波器。是使用最普遍、最有成效的一种模拟滤波器变数字滤波器的工具。这是因为大部分的滤波器与本设计的低通滤波器相同都具有分段常数的频响特性，其在通带内要求逼近一个衰减为零的常数特性，而在阻带部分要求逼近一个衰减为∞的常数特性，这种特性的滤波器通过双线性变换后，虽频率发生了非线性变化，但幅频特性仍保持分段常数的特性。

2心电信号检测中滤除肌电干扰方法

肌电干扰属于高频干扰，设计选用切比雪夫数字低通滤波器。具体步骤是：首先设计切比雪夫型的模拟低通滤波器，再将该模拟滤波器转换为数字滤波器。设计用到的技术指标：心电信号通带截止频率ωp；阻带截止频率ωs；通带最大衰减系数αp；阻带最小衰减系数αs.对于肌电干扰ωp=ωs=αp=1 dB，αs=15 dB.

2.1切比雪夫型模拟低通滤波器的设计

首先进行归一化处理，然后联立关于通带和阻带最大衰减系数的方程求解ε和N，将其代入到|H（jλ）|2，继而求解归一化传递函数H（p），其中p是归一化频率λ对应的拉氏变量，解得

2.2将模拟转变为数字滤波器

该方法在变换公式中s与z的关系无论是分子还是分母部分均为线性的，其主要优点是消除了脉冲响应不变法所固有的频谱混叠现象。

将模拟低通滤波器的传递函数化为

由此便完成了模拟到数字的转换，进而构成滤除肌电干扰的切比雪夫数字低通滤波器设计。

3仿真设计

3.1对肌电干扰的抑制效果

根据以上对肌电干扰噪声的分析结合切比雪夫数字低通滤波方法，在Matlab程序当中输入对应的参数进行仿真，仿真结果如图1所示。

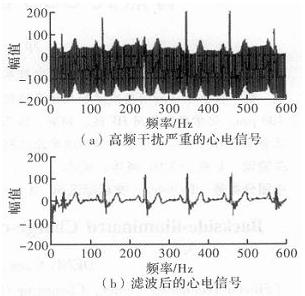
图1 心电信号受干扰前后对比图

3.2验证与分析

为验证本次设计滤波器的有效性和实用性，此处采用图2所示受到严重干扰的心电信号进行试验，验证结果如下。

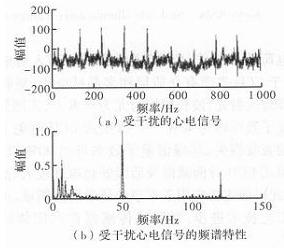
图2 滤波前的心电信号及其幅频特性

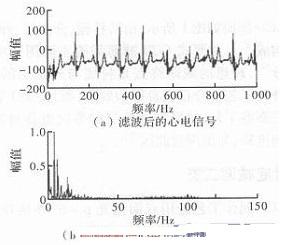
图3 滤波后的心电信号及其幅频特性

从图3中可看出，滤波后心电信号中的肌电干扰即高频干扰部分得到了明显的抑制，虽在100 Hz附近仍存在小范围干扰，但从滤波整体效果上看，该滤波器是满足设计要求的。

4结束语

本设计以数字滤波为依据，结合Matlab进行软件程序设计，进而实现了对肌电干扰滤波器的设计。该设计程序有效性高、实用性强，且能够较好地滤除肌电干扰，大幅提高了心电信号检测的准确性，为其在临床中更好地诊断治疗提供了帮助。