摘要：采用跨层优化方法，分析了无线传感器网络点对点链路的吞吐量优化问题。首先推导出吞吐量的理论表达式；随后以最大化吞吐量为目标，采用一种基于分层优化的数学框架，分别得到物理层最优符号速率、最优调制星座体积和MAC层最优数据包长；在此基础上，通过联合优化物理层参数和MAC层参数实现了链路吞吐量的最大化；最后提出了一种自适应跨层优化策略。在不同的信噪比条件下，根据该自适应策略来配置相应的最优物理层参数和MAC层参数，便可以保证链路的吞吐量达到最优值。仿真结果表明，与传统的分层优化相比，跨层优化后链路的吞吐量性能得到了明显提高。

关键词：无线传感器网络；移动性；吞吐量；跨层优化

引言

吞吐量是无线传感器网络(Wireless Sensor Network，WSN)的一项重要性能指标，它直接反映了无线传感器网络工作运行的效率，如何提高吞吐量一直都是无线传感器网络研究的热点。

R．J．Lavery在参考文献中首次建立了经典的Adhoc网络点对点链路模型，明确了点对点链路模型吞吐量的数学定义式。作者以吞吐量为优化目标，针对影响吞吐量的符号速率和数据包长度这两个参数分别作了优化，得到了不同条件下的最优符号速率和数据包长。随后Taesang Yoo等人在参考文献中提出了一种数学框架，采用符号速率、数据包长度、调制星座体积3个参数作为优化变量，实现了MQAM调制方式下点对点链路吞吐量的优化。其后的参考文献基于参考文献提出的模型和假设，对链路的吞吐量也作了类似的研究和优化分析。但是参考文献的吞吐量优化都是基于参考文献建立的Ad hoc网络点对点链路模型，而目前针对无线传感器网络吞吐量的研究相对较少。

针对上述问题，本文将针对在WSN中如何最大化点对点链路吞吐量这一问题展开研究。为了最大化吞吐量，本文采用跨层优化机制，不仅考虑了符号速率和调制星座体积这两个物理层(PHY)主要参数，还考虑了MAC层的数据包长度，通过PHY和MAC层参数的联合优化，保证在不同通信距离下链路的吞吐量能够达到最优。

1 系统模型和假设

为了简化分析，本文只考虑WSN中两个通信节点之间的点对点链路。WSN中点对点通信链路一般由单个的发射机、接收机以及无线通信信道组成。假定发射机节点发送的每个数据包总长为K+C=L位，其中K为有用信息数据长度，C为循环冗余校验码CRC(Cyclical Redundancy Che ck)，用来检测每个数据包中的误码，在本文的仿真分析中C=16位。接收机节点使用CRC校验接收到的数据包。假定CRC只进行检错而没有进行纠错编码，并且CRC有足够的冗余度可以检测到每个数据包的所有误码。当接收机接收到的数据包中不包含误码时，便发送一个ACK反馈帧给发射机，告之数据已经正确接收；否则发送一个NACK反馈帧。当发送节点接收到NACK帧时，便重传该数据包，否则传送下一个新的数据包。在实时通信中，ACK仍有可能产生误码，从而导致系统的吞吐量下降。为了简单起见，这里假定ACK／NACK反馈帧在传输过程中不会出现误码。

根据参考文献，点对点链路的吞吐量可以定义为：每秒成功接收到的有用信息比特数。对于一个基于上述模型和假设条件的点对点传输链路，其吞吐量通式为：

其中，b为每个调制符号所包含的比特数，Rs为符号速率，f(b，rs，L)为包成功传送率(PSR)，它定义为正确地接收到一个数据帧的概率。PSR由下式给出：

其中Pr为信号接收功率，N0为AWGN信道中噪声的半边功率谱密度。

同时，接收信噪比定义为：SNR=Pr／(N0·B) (4)

其中B=1 MHz为系统带宽。比较式(3)、(4)，可以得到符号信噪比rs与接收信噪比SNR之间的关系为：

2 吞吐量分层优化

2．1 物理层参数优化

2．1．1 符号速率优化

为了找到最优符号速率，以使得链路的吞吐量达到极大值，对式(1)求关于Rs的偏导数并令该导数为0，即令，可以得到如下关于rs的微分方程：

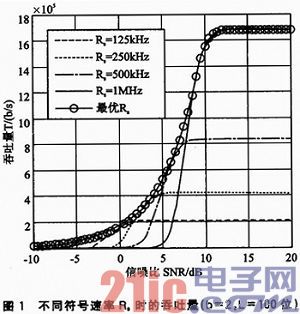
图1给出了4种不同符号速率条件下，吞吐量与SNR的关系曲线。可以看出，当SNR较高时，链路能够支持较高的符号速率，从而获得较大的吞吐量；然而当SNR低于一定值时，吞吐量迅速减小，此时应采用较低符号速率以维持一定的吞吐量。因此，在实际的通信系统中，为了得

到最优吞吐量，必须根据SNR进行自适应速率调整。根据式(8)可求解得到当L=100、b=2时，。当SNR发生变化时，应根据式(9)来调节数据速率Rs，确保，以保证得到最优吞吐量。据此得到的最优吞吐量曲线如图1所示。

2．1．2 调制星座体积优化

从式(7)、(8)可以看到，调制星座体积b对Pe、rs也有影响，因而链路的最优吞吐量也取决于调制星座体积的大小。同样，对式(1)求关于b的偏导数，并令，可得：

由上式可知，b*取决于L、Pe和rs，而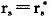时，b*仅取决于L和Pe；根据不同调制方式下的误符号率Pe，通过求解(10)式，可得该调制方式下的b*。

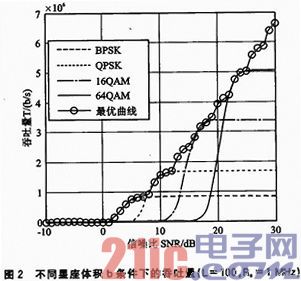
图2显示了不同信噪比条件下，星座体积b对吞吐量的影响。由图2可见，当信道条件较好，即SNR较大时，可以让每个符号承载更多的信息位，即采用高阶调制方式来提高系统的吞吐量；而当信道条件较差即SNR较小时，误符号率较大，此时应该采用低阶调制方式，以保证最优吞吐量。

2．2 MAC层优化

在Rs及其他系统参数一定的条件下，可以找到一个使吞吐量最大的包长，称为最优数据包长度，记做L*。L*可以用求极值的方法得到，对式(1)求关于L的偏导数，令，可求解得到最优数据包长度：

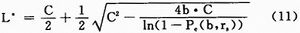
图3比较了在不同SNR、不同包长L条件下链路吞吐量。如图3所示，当SNR较大时，包长越大，吞吐量越大。这是因为，较近的通信距离使得信道条件比较好，信噪比较大，误包率非常小，f(b，rs，L)≈1。此时吞吐量T≈bRs(L—C)／L，即吞吐量与SNR无关，而是随着L的增大而增大。但是吞吐量不会随着L的增大而无限增大，当L>>C时，T≈b·Rs，即T的上限值为b·Rs。以上两点结论均可从图3中得到很好的验证。但是L不宜过大，因为若L过大，可能会引入其他的问题，譬如延时等。因此，要权衡时延等因素而选取一个尽可能大的数据包长度L，在本文仿真中设定最大包长Lmax=512。

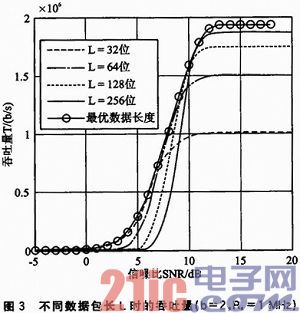
然而，从图3中还可以看到，随着SNR低于一定值时，吞吐量迅速下降为0。此时，求解式(11)得到不同通信距离下相应的最优数据包长L(d)*，进而得到吞吐量的最优曲线，如图3所示。从最优曲线可以看到，当SNR<2 dB时，T≈0，此时即使采用最优数据包长，提高不了吞吐量。因此，信道条件较差时，仅靠MAC优化并不能使吞吐量最大化。

3 物理层和MAC层跨层联合优化及自适应

在2．1～2．2节的分层优化中，只能求得吞吐量的极大值。为了使链路的吞吐量最大化，必须联合物理层和MAC实现跨层优化，即在WSN中，根据接收信噪比SNR和分层优化中所推导出的最优等式，计算出最优配置参数，然后自适应地在物理层调整Rs和b值，在MAC层调整L值。最优配置参数可联立求解最优等式(7)、(10)、(11)而得到：

从图1～图3的分层优化仿真图中可以看到：当SNR较大时，优化后的吞吐量的大小关系为T(b)>T(L)>T(Rs)；而当SNR低于一定值后，优化后的吞吐量的大小关系为T(Rs)>T(b)>T(L)。特别地，当SNR<2dB时，T≈0，调节L或b均已经失去优化能力；而从图1中可以看到，优化Rs后链路仍能获得不错的吞吐量性能。因此，为了使链路在不同的信噪比条件下都能有较高的吞吐量，必须进行跨层优化。

跨层优化后的最优吞吐量曲线如图4所示，同时给出了两种次优吞吐量曲线，以便进行对比分析。从图中可以看到，两条次优吞吐量曲线分别在较高信噪比(SNR>2dB)和较低信噪比(SNR<2 dB)条件下，与最优吞吐量曲线取得一致。因此，为了保证链路的最优吞吐量，可采取如下自适应调节策略：

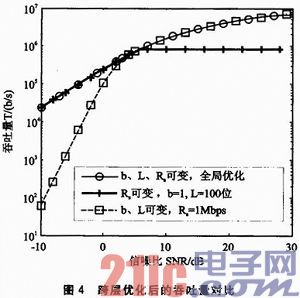
①高信噪比(SNR>2 dB)区：在此区域内信道条件相对较好，误符号率很低，应尽可能采用高的符号速率；但由于受系统带宽的限制，Rs ≤B，所以单方面通过增大符号速率并不能使吞吐量达到最优。此时，可以通过让每个符号承载更多的位信息，即采用高阶调制方式以提高系统的吞吐量并联合最优数据包长，可使吞吐量达到最优。最优参数对(b*，L*)可以通过联立求解式(10)、(11)得到。

②较低信噪比(SNR<2 dB)区：在此区域内信道条件急剧恶化，误符号率Pe较大，此时应以尽量降低Pe为主。由式(8)知，MQAM调制的误符号率主要取决于b和rs，为了尽可能降低Pe，应该采用BPSK，即b=1；同时调节符号速率Rs以使。由式(11)可求解得到在此区域内应采用的最优数据包长L(d)*=L(b=1，rs*)。

通过上述自适应策略来配置相应的参数组(b，L，Rs)，便可以保证在不同的信噪比条件下，链路的吞吐量始终能达到最优值。

结语

吞吐量是衡量无线传感器网络服务质量(QoS)好坏的重要标准。针对移动性无线传感器网络点对点链路的吞吐量问题，本文采用跨层优化分析的方法，定量地描述了两个移动节点之间无线通信链路的吞吐量表达式。根据吞吐量表达式，选择优化后的物理层参数符号速率Rs、调制星座体积b和MAC层参数数据包长度L，可以优化链路吞吐量。最后提出了一种能够根据节点间通信距离自适应跨层调节的优化策略。根据该跨层优化策略自适应调节物理层和MAC层参数，保证了在不同通信距离下链路的吞吐量始终保持最大化。

在进一步的研究工作中，将建立多跳移动性无线传感器网络吞吐量模型，并研究该模型下的吞吐量优化问题。