摘要：DV-Hop算法是无线传感器网络中一种典型的基于非测距的定位算法。针对DV-Hop存在的定位精度低的缺陷，本文提出了改进的算法。该算法中的平均跳距利用全网平均跳距与单个锚节点估计的平均跳距的均值来修正，并且根据连通度不同，选取最优的3个锚节点进行三边定位计算。

关键词：无线传感器网络；DV—Hop算法；平均跳距；连通度的不同；三边定位；定位精度

引言

无线传感器网络是由大量随机分布的传感器节点组成，是一种分布式的、自组织的网络。其关键技术包括：网络拓扑控制、节点定位、时钟同步、数据融合、路由协议等。而节点定位问题则是无线传感器网络中的一个最为基本和重要的问题。目前，无线传感器网络定位算法可以分为基于测距和基于非测距的定位算法。基于测距定位常用的测量方法有TOA、TDOA、AOA、RSSI，尽管这些技术相对精度高，但是对硬件要求很高。基于非测距定位常用的测量方法有：DV-Hop、质心、APIT、MDS—MAP。

DV—Hop为典型的基于非测距定位，其对硬件要求低，实现简单。它的不足之处在于计算平均跳距及定位坐标时会产生误差。因此针对DV—Hop算法的缺陷，提出了一系列的改进算法，参考文献对原始算法中的平均跳距进行改进，使用多个锚节点估算平均距离并且采用归一化加权的平均跳距。参考文献提出了基于几何学的定位算法，利用几何学中的斜率方法来判断锚节点间的位置关系，从中选取最优的锚节点序列，从而更精确地确定未知节点。参考文献引入共线度的概念，利用共线度参数，动态地调节未知节点可以收集的邻居锚节点的距离阈值，挑选网络中好的锚节点组进行位置估计，最后再用加权估计机制来得到最终的节点位置估计。这些方法都在一定程度上提高了定位精度。

本文针对DV—Hop算法中计算平均跳距和三边定位两方面存在的定位误差，提出了改进的算法。首先利用全网平均跳距来纠正单个锚节点的平均跳距，然后在最后计算三边定位时，利用节点间连通度的不同，选择最优组合的3个锚节点来参与定位，进一步提高定位精度。

1 DV—Hop算法介绍

美国路特葛斯大学的Dragos Niculescu等人利用距离矢量路由和GPS定位原理提出一系列分布式定位算法，合称APS，DV—Hop算法就是其中的一种。

DV—Hop分为3个步骤实现：

①锚节点i广播自身的位置信息IDi。初始跳数0，每发送一个节点信息，跳数就加1，然后转发，直到网络中所有的节点都收到锚节点的信息包。如果节点收到同一个锚节点不同的跳数信息，只取最小的跳数信息。

②当锚节点i接收到其他锚节点的位置和最小跳数信息后，就可以计算出平均每跳距离(Average Hop Distance，AHD)的计算公式：

其中，(xi，yi)、(xj，yj)分别为锚节点i、j的坐标；hij为两个锚节点之间的跳数。未知节点只接收离它最近的锚节点的AHDi，hopi为未知节点离最近锚节点的跳数，再根据跳数信息，即可算得未知节点与锚节点的距离P：

P=AHDi×hopi (2)

③当未知节点获得3个或者更多的锚节点信息时，可以利用三边定位或者最大似然相似求出未知节点的位置。(x，y)为未知节点的坐标，(xi，yi)为已知锚节点的坐标。根据式(2)即可算出未知节点的坐标：

2 改进后的DV—Hop算法

本文主要对DV—Hop算法里的第2步和第3步进行改进，第1步与原算法相同。原算法中，在第2步计算平均跳距的时候，未知节点接收来自最近的锚节点的平均跳距。但是由于网络节点分布的不均匀性，导致单个锚节点计算的平均跳距存在着一定的误差，因此本文引入全网平均跳距与单个锚节点平均跳距的均值来修正原算法中的平均跳距。在第3步中，锚节点的位置信息对定位精度影响很大，本文利用节点间连通度的不同，选取最优的3个锚节点，以减小定位误差。

2．1 平均跳距的改进

将全网平均跳距与单个锚节点估算出来的AHDi取平均来代替经典算法中的平均跳距，这样未知节点既有全网的估算信息，也具有离它最近的锚节点的估算平均跳距AHDi的局部信息。全网平均跳距公式为：

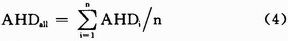
其中，n为网络中的锚节点的个数。

修正后的平均跳距AHD公式为：

AHD=(AHDall+AHDi)／2 (5)

2．2 基于选择性的3个锚节点

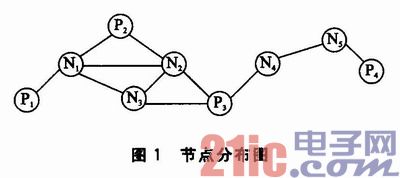
基于选择性的锚节点的定位算法利用连通度的不同，在三边节点定位时，选择最优的3个锚节点定位，使其定位误差最小。节点分布图如图1所示。未知节点N1利用三边定位时可以用不同的3个锚节点组(P1，P2，P3)、(P1，P2，P4)、(P2，P3，P4)、(P1，P3，P4)来定位。而用最大似然估计计算时，则选用(P1，P2，P3，P4)来定位，这样不同的锚节点组肯定会产生不同的定位位置。

2．2．1 基本规则

用未知节点与每个锚节点的最小跳数来定义连通度，用数组来表示。比如N1到所有锚节点的连通度为[1，1，2，5]。这样图1中的所有的未知节点的连通度可以用数组表示，如表1所列。

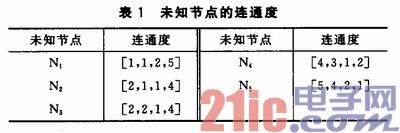
用未知节点之间连通度差的绝对值的和来定义连通度的不同，比如N1与N2之间连通度的不同为|1—2|+|1—1|+|2—1|+|5—4|=3。这样可以计算N1到其他所有未知节点的连通度的不同，如表2所列。

由表2可以得出，N2、N3到N1连通度不同为3、4，而N4、N5到N1连通度不同为9、11。说明N1离N2、N3更近。这一点也可以从图1中看出。

2．2．2 确定最优的3个锚节点

选择性锚节点的节点分布图如图2所示。未知节点Nx代表未知节点的实际位置，N(i,j,k)为根据3个锚节点组合所估算的位置，R为节点的通信半径，An是离N(i,j,k)最近的锚节点，Am为通信范围R之外的任意锚节点。

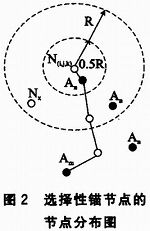
An的位置情况有3种：在0．5R的通信范围内；在0．5R～R的通信范围内；在R通信范围之外。这样计算AHD(i,j,k)，m就有3种可能：

其中，AHD(i,j,k),m为根据3个锚节点组合所估算的位置节点与锚节点Am之间的平均跳距，AHDn,m为锚节点An与锚节点Am之间的平均跳距，AHDm为锚节点Am的平均跳距。

N(i,j,k)与锚节点Am之间的距离P(i,j,k)，m可以计算出来，那么就可以算出N(i,j,k)与锚节点Am之间的跳数hop(i,j,k)，m，公式为：

假设一共有n个锚节点，这样N(i,j,k)与Nx计算出来的连通度的不同可以表示为

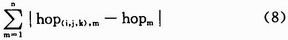
Nx选出最小的连通度不同的节点是最为靠近Nx的节点(即定位的误差最小)。

3 算法仿真实验

为了验证算法理论的可行性，在100 m×100 m的区域中，对提出的改进的DV—Hop算法用Matlab7．0进行实验仿真，将实验结果与原DV—Hop算法和参考文献的算法进行对比分析。仿真数据随机运行50次，最后取平均值。

3．1 测距误差

测距误差是指节点间的估算距离与实际距离的差值。在100 m×100 m的区域中，随机分布100个节点进行仿真实验，其中有一部分部署的是锚节点，是能够获知自身位置信息的节点，且锚节点和未知节点具有相同的通信半径。通过设置不同的锚节点比例和节点通信半径，比较改进的算法与原DV—Hop算法对测距误差的影响。图3为通信半径为10 m时的测距误差，图4为通信半径为20 m时的测距误差。

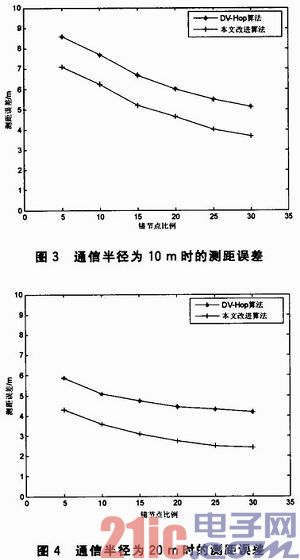
在同等条件下，改进的测距误差始终是低于原DV—Hop算法的，且不同的通信半径对测距误差也会产生不同的结果。图3中，通信半径为10 m，改进后的算法平均测距误差比原算法降低1．45 m；图4中，通信半径为20m，改进后的算法平均测距误差比原算法降低1．67 m。这是因为随着通信半径的变化，会对节点间的跳数和平均跳距产生影响。由于本文改进后的算法是用全网的平均跳距代替单个节点的平均跳距，这样使得对平均跳距的估计更为准确，估算距离也就越准确，越接近实际的距离。

3．2 定位误差

定位误差(Localization Error，LE)是指通过定位算法测量估计的坐标与实际坐标之间的差值，用这种差值除以节点的通信半径，就是定位误差率。计算方法如下：

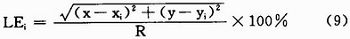
其中，(x，y)为未知节点的实际坐标，(xi，yi)为定位算法所估计出来的坐标；R为节点的通信半径。

图5和图6是节点总数分别为100和300、节点通信半径为10 m时，本文改进算法、DV—Hop算法和参考文献中的算法三者在锚节点比例不同时的定位误差比较结果。从两幅图中可以看出，在相同的半径和锚节点的环境下，改进算法的定位误差率要低于DV—Hop算法和参考文献中的算法。但是在锚节点比例较低的情况下，节点的定位误差较大。这是因为锚节点较少时，未知节点与锚节点之间的距离变远，导致计算平均距离时会产生很大的误差。因此随着锚节点比例的增加，能够有效地减小定位误差。

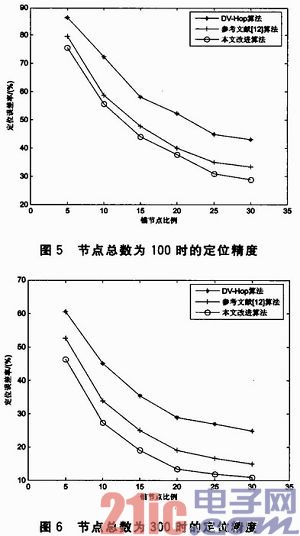
图5中，当锚节点的比例为30％时，DV—Hop的定位误差率为43．25％，参考文献算法的定位误差率为33．37％，而本文改进算法的定位误差率为28．34％。图6中，当锚节点的比例为30％时，DV—Hop的定位误差率为26．89％，参考文献算法的定位误差率为14．95％，而本文改进算法的定位误差率为10．21％。由此说明，本文的改进算法要优于其他两种算法。这是因为在参考文献中，只考虑了平均跳距一个因素对定位误差的影响，而本文改进算法则是从平均跳距的改进和利用连通度的不同选取锚节点两个方面考虑，使其定位误差进一步地减小。

结语

本文首先介绍了DV—Hop算法的基本思想，针对经典的DV—Hop算法中存在的定位精度不高的缺陷，提出了两点改进：

单个锚节点所估计的平均跳距来代替全网的平均跳距，会产生很大的误差，因此平均跳距利用全网平均跳距与单个锚节点估计的平均跳距的均值来修正；

根据连通度的不同选择最优的三个锚节点进行三边定位计算，以提高定位精度。

仿真实验数据表明，改进后的算法降低了测距误差，与参考文献等提出的算法比较，定位误差率进一步降低，从而提高定位精度。且在改进的过程中，没有添加硬件成本。