摘要：针对直接转矩控制(DTC)数字控制系统采样与控制时延所造成的电机转矩与磁链纹波增大的问题，提出一种应用于永磁同步发电机(PM SG)的预测DTC策略。通过建立PMSG的数学模型，深入分析控制系统的时延机理，建立了基于电机模型方程的转矩与磁链预测算法。最后构建了PMSG实验机组，实验结果表明，该预测策略在保持传统DTC优良动态性能的基础上，可有效减小转矩纹波，系统性能得到提升。

关键词：永磁同步发电机；直接转矩控制；时间延迟

1 引言

以风力发电为代表的可再生能源得到广泛关注，其中基于双馈感应发电机与PMSG的风电系统应用最为广泛。由于PMSG风电系统具有运行

效率高、调速范围宽等优点，且无需齿轮箱、滑环与电刷等，已成为大功率、海上风电领域极具潜力的发展方向。

为满足PMSG的高性能运行需求，DTC作为一种先进的交流电机控制策略，应用于风电领域极具优势。其中基于空间矢量调制(SVM)的DTC具有开关频率恒定、转矩纹波较小等优点。为改善传统DTC较大的转矩与磁链纹波，可采用基于开关表方法的预测DTC技术，但其控制算法较复杂，且无法克服开关频率不固定等问题。

为提高PMSG运行性能，在此建立PMSG数学模型，在分析控制系统采样延迟的基础上，提出一种基于SVM的预测DTC策略。通过搭建的PMSG实验机组，对所提方案进行了实验验证。

2 PMSG预测直接转矩控制

2．1 PMSG数学模型

两相静止α，β坐标系下PMSG的定子电压、磁链数学模型为：

2．2 预测直接转矩控制策略

传统DTC算法中，定子磁链与电磁转矩是根据当前采样点(假定为k时刻)的电压u(k)与电流值i(k)由式(1)，(2)算得，并根据DTC策略得到相应的目标电压矢量v(k)。理想情况下该电压矢量在k时刻施加，在k+1时刻使转矩与磁链达到给定值，如图1a所示。但由于采样及数字计算的延迟，期望电压矢量实际上是在一个采样周期后，即k+1时刻施加，在k+2时刻才使转矩与磁链达到给定值，如图1b所示。这使得转矩与磁链的响应始终滞后一个开关周期，降低了PMSG系统的运行性能。

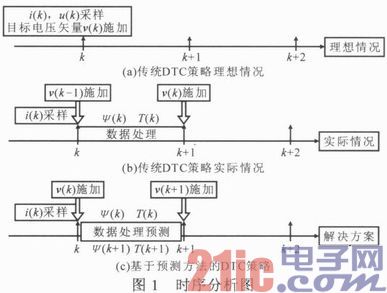
对此，这里给出一种基于预测方法的DTC策略，如图1c所示。根据k采样时刻电压电流值计算出定子磁链与转矩值，根据PMSG模型对k+1时刻的磁链与转矩值进行预测，进而选出合适的电压矢量。这样在k+1时刻，施加的电压矢量为v(k+1)，当k+2时刻到来时，使得k+2时刻的磁链与转矩值刚好达到给定，以解决由于时间延迟带来的转矩与磁链纹波较大等问题。

2．3 预测算法

为改善由于时间延迟导致PMSG运行性能下降的问题，需在DTC中加入对转矩和磁链的预测。由式(1)可得定子磁链的预测表达式为：

若能推导出isα(k+1)与isβ(k+1)，根据式(2)便可得到k+1时刻的转矩值，但由于所研究的PMSG为凸极电机，难以在α，β轴下求解电流值，鉴于此可在d，q旋转坐标系下对电流进行预测。

PMSG在d，q旋转坐标系下的电压方程为：

根据式(5)可预测k+1时刻的电流值，然后对其进行反Park变换(变换时需要转子位置信息θ，θ值由无位置传感器获得)，即可得到α，β轴

下电流的预测值，结合式(2)，(3)即可计算出k+1时刻的转矩预测值：

Te(k+1)=3np[ψsα(k+1)isβ(k+1)-ψsβ(k+1)isα(k+1)]／2 (6)

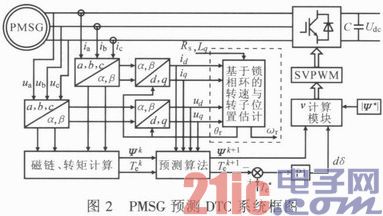
图2示出基于SVM的PMSG系统预测DTC框图，虚线框中为使用无位置传感器技术获得的转子位置与转速信息，预测算法模块使用式(3)～式(6)获得k+1时刻的转矩与磁链值，其他部分与常规SVM-DTC类似，通过SVPWM实现对机侧变流器的控制。

3 实验验证

为验证基于SVM技术的PMSG预测DTC策略，搭建了一套5．5kW PMSG控制系统，如图3所示。风力机模拟平台参数：感应电机功率7．5kW；电机极对数2；齿轮箱变比17：1。PMSG参数：额定功率5．5 kW；额定线电压230 V；额定电流19．5 A；额定转速80 r·min-1；极对数8；d轴电感77．56 mH；q轴电感107．4 mH；定子电阻1．1 Ω；直流母线电压260 V；额定转矩656 N·m。使用通用变流器控制的7．5 kW感应电动机作为风力机模拟平台，通过齿轮箱降速与额定功率为5．5 kW PMSG相连。PMSG由机侧变流器实现发电控制，由于在实际风力发电系统中直流母线电压通常由网侧变流器来提供，并维持恒定，在此通过直流电源作为直流母线供电电源，并在直流母线上并联电阻Rdc作为系统负载，用来消耗PMSG发出的电能。

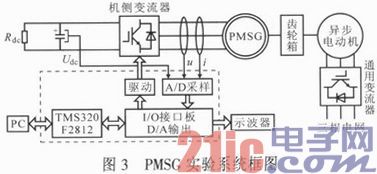
图4a，b为PMSG在传统DTC和预测DTC下的稳态转矩与电流波形，其中转速为40 r·min-1，转矩给定为-350 N·m，电流有效值为7．4 A，此时PMSG输出功率为1．5 kW。可见，传统DTC下，实际转矩在给定转矩值上下波动，纹波水平约为8％，电流THD值为7．29％；预测DTC下，转矩纹波明显减小，约为给定值的4％，电流THD值为5．9％，相比于传统DTC有所改善。

图4c，d示出PMSG在传统DTC与预测DTC下的动态响应波形，转矩均从-350 N·m阶跃至-150 N·m，同时电流值也相应地减小，预测DTC和传统DTC下响应时间分别为6．3 ms和6．5 ms，可见所提出的预测DTC策略保留了传统SVM-DTC优良的动态特性。

4 结论

由于DTC策略在每个采样周期内均需进行数据处理，导致相应的采样与控制时间延迟，增大了转矩与磁链的控制误差。为此提出一种基于空间矢量调制技术的PMSG预测DTC策略，该方案通过对转矩和磁链的预测，可有效弥补时间延迟对系统性能的影响。实验结果表明，该预测算法可有效减小转矩纹波，同时也保留了传统空间矢量调制DTC优良的动态特性，提高了系统性能。