摘要：依据已经提出的电压阀和电流阀两种非线性电路模型以及由电压阀和电流阀构造出的晶体管模型，进一步对各种晶体管放大电路进行了非线性模型等效，并在等效的模型电路基础上，研究晶体管放大电路的静态工作点计算方法、动态参数计算方法。该方法具有电路直观、概念清晰、分析计算准确等特点，而且能够判断出晶体管是否截止或饱和、动态工作范围大小等。

关键词：电压阀；电流阀；晶体管放大电路；非线性模型

0 引言

以往的模拟电路对于晶体管放大电路的分析，由于没有能够将静态特性和动态特性统一为一体的电路模型，静态分析和动态分析需要分别使用不同的电路模型，对分析计算和概念理解均带来很多不便。依据已经提出的电压阀和电流阀两种非线性电路模型，可以建立起晶体管的等效电路模型，这种模型能比较全面地反映出晶体管的直流和交流特性，且适用范围可以包括晶体管的截止、放大和饱和三个区域。于是，通过该晶体管等效模型对晶体管放大电路进行模型化处理后，得到的等效电路将可以用于晶体管放大电路的静态工作点计算、晶体管放大电路的动态参数计算以及晶体管开关工作状态下的电路计算。

1 晶体管放大电路分析与计算

1．1 输入端与输出端之间不存在反馈的晶体管电路计算

设有晶体管放大电路如图1(a)所示，晶体管基极一发射极间的导通开启电压为Uon，基区体电阻为rbb，放大倍数为β。试分析电路的工作状态，并计算电路的静态工作点Q和动态参数。

根据晶体管等效电路模型，将图1(a)所示的晶体管电路表述为图1(b)所示的模型电路形式。模型电路中，电压阀V1的阈值电压Uz等于晶体管发射结的开启电压Uon，受控电流阀V2的限制电流Iz=βIb。

(1)静态分析

令电压阀V1开路，则可知电压阀两端电压为正向电压Ui。当Ui小于电压阀阈值电压Uz时，电压阀将截止，Ib=0，同时导致Iz=0，受控电流阀也处于截止状态，故Ic=0，输出电压Uo=VCC。这实际上是晶体管的截止状态。

当Ui大于电压阀V1阈值电压Uz时，电压阀将导通，有：

于是，若外电路产生的试图流过电流阀的电流时，电流阀将处于限制状态，使电流Ic=Iz，静态输出电压：

UCE=VCC-IcRc (6)

这就是晶体管的放大状态。Ib，Ic和UCE即指示了放大电路的静态工作点Q，故也常将这三个参数称为IBQ，ICQ和UCEQ。

若外电路产生的试图流过电流阀的电流时，电流阀V2将呈导通状态，使，输出电压Uo≈0。这实际上是晶体管的饱和状态。

(2)动态分析

对于处于放大状态的晶体管电路可进行动态分析。

设自晶体管电路输入端加入一个为△Ui的交变信号，因电压阀V1的阈值电压恒为Uon，而直流电压Ui已大于Uon，故交变信号△Ui可通过电压阀V1，引起的输入电流变化量为：

求输出电阻时，可令VCC=0，Ui=0，即电源两端均视为短路，从输出端加上电压△Uo，根据输出端电流△Io可知输出电阻为Rc。

在电路中，即近似为晶体管集电极电流Ic的饱和电流。若将晶体管静态工作电流ICQ设为等于，则Ic的动态范围也近似为。

1．2 输入端与输出端之间存在反馈的晶体管电路计算

设有晶体管放大电路如图2(a)所示，晶体管基极-发射极间的导通开启电压为Uon，基区体电阻为rbb，放大倍数为β。试分析电路的工作状态，并计算电路的静态工作点Q和动态参数。

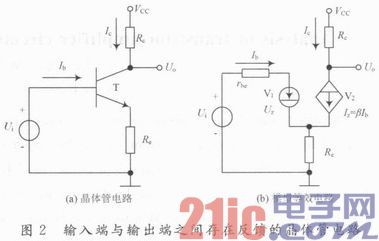
根据晶体管等效电路模型，将图2(a)所示的晶体管电路表述为图2(b)所示的模型电路形式。模型电路中，电压阀V1的阈值电压Uz等于晶体管发射结的开启电压Uon，受控电流阀V2的限制电流Iz=βIb。

(1)静态分析

假设晶体管处于放大状态，即流过受控电流阀的电流等于限制电流：

再由式(2)可求得rbe。若Ib>0，则表示晶体管处于非截止状态。此时，还需进一步验证晶体管是否处于放大状态。若：

Ic=βIb<VCC／(Rc+Re) (16)

表明晶体管处于放大状态，否则表明晶体管处于饱和状态。处于放大状态时：

UCE=VCC-Ic(Rc+Re) (17)

(2)动态分析

对于处于放大状态的晶体管电路可进行动态分析。

设自晶体管电路输入端加入一个为△Ui的交变信号，引起的输入电流变化量为：

输出电阻仍为Rc。

如若在电阻Re上并联有足够大的电容C，则模型电路被描述为如图3所示的等效电路。

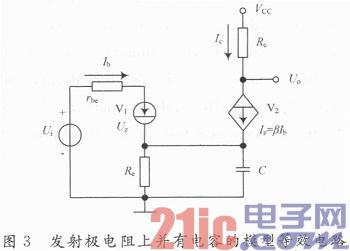
由于电容C具有隔直流、通交流的特性，故其静态分析过程和结果仍与1．2节的静态分析相同，而电路的动态分析的过程和结果则同于1．1节的动态分析。

2 结论

由以上分析可见，利用电压阀和电流阀两种非线性电路模型构造出的晶体管模型，能够将晶体管放大电路比较准确地等效为电路模型，而依据这一等效电路模型则可以进行电路的静态分析和动态分析，将电路的静态分析和动态分析有机的结合在一起，避免了以往模拟电路中静态分析和动态分析要使用不同的模型电路所带来的不便，使电路的分析和计算方法得到了发展。