《线性及开关电源的控制环路设计》是Power Electronics前专栏作者Christophe Basso的最新著作。此著作注重探讨工程师真正需要了解的补偿及稳定给定控制系统的知识。本文包含此书有关稳定性标准章节的摘录内容。

在电子领域，振荡器是一种能够产生自激正弦信号的电路。在多种多样的配置中，振荡器的加速过程牵涉到采用振荡器的电子电路固有的噪声。上电时噪声等级上升，此时开始振荡及自激。此类电路可采用图1所示的构成模块组成。如您所视，此配置看上去非常接近于我们控制系统的配置。

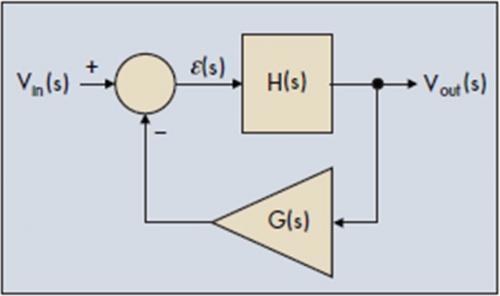
图1：振荡器实质上是一种误差信号，不会妨碍输出信号变化的控制系统。

在我们的示例中，励磁输入并非噪声，而是电压电平Vin，它被注入为输入变量以启动振荡器。直接通道由传递函数H(s)构成，而返回通道包含G(s)区块。要分析此系统，我们首先通过输出电压与输入变量的变化关系方程式来写出其传递函数：

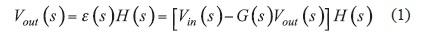
如果我们扩充此公式及Vout(s)项，我们就得到

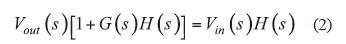
故此类系统的传递函数就是：

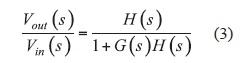
在此方程式中，乘积G(s)H(s)称作环路增益，其标记为T(s)。要将我们的系统转换为自激振荡器，则必须存在输出信号，即使输入信号已消失。为了满足这样的目标，就必须符合下列条件：

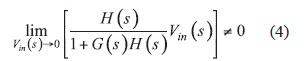
要在Vin消失条件下验证此方程式，商数(quotient)就必须无限大。商数无限大的条件就是特征方程式D(s)等于0：

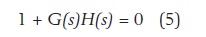
要满足此条件，G(s)H(s)必须等于-1。换句话说，环路增益的大小就必须为1，其符号应当改为负号。正弦信号的符号改变只不过是相位翻转180°。这两个条件能以下面两个方程式来进行数学表述：

图2：振荡条件能以波特图或奈奎斯特图来表述。

在满足这两个方程式的条件下，我们就得到稳态振荡条件。这就是所谓的巴考森(Barkhausen)标准，由德国物理学家Barkhause在1921年提出。实际上讲，在一个控制环路系统中，它表示修正信号不再抗拒输出，而是相位形式返回，振幅恰好与励磁信号相同。方程式(6)和(7) 在波特图(Bode plot)中表示环路增益曲线，此曲线穿过0 dB轴，且恰好在此点受180°相位滞后影响。在奈奎斯特分析中，环路增益的虚数及实数部份相对频率的变化关系被绘制成图，此点对应于-1, j0。图2显示了满足振荡条件的两个曲线。如果系统略微偏离这些值(如温度漂移、增益变化)，输出振荡要么会以指数形式下降至0，要么振幅发散，直到达到较高或较低的电源轨。在振荡器中，设计人员竭力尽可能多地降低增益余量，使振荡条件在多种工作条件下都能满足。

稳定条件

如您所知，控制系统的目标不是构建振荡器。我们希望控制系统提供高速、精确及无振荡的响应。因此，我们必须避开满足振荡或发散条件的配置。一种方式是限制系统会作出反应的频率范围。就定义而言，频率范围或带宽，对应于从输入到输出之闭合环路传输通道下降3 dB的频率。闭合环路系统的带宽能被视作频率范围，在此范围内系统被认为会极佳地响应其输入(即遵循设定点或有效地抑制扰动)。我们在后文会看到，在设计阶段，我们并不直接控制闭合环路带宽，但会控制交越频率(crossover frequency) fc——这是一项跟开环路分析有关的参数。这两个变量通常被概略认为相等，但我们会看到这仅在一种条件下成立。然而，它们相差得也不太远，在讨论中这两项能互换。

我们已经看到，开环路增益是我们系统中的一项重要参数。当增益存在时(即|T(s)|>1)，系统以动态闭合环路工作，能补偿输入的扰动或对设定点变化作出反应。然而，系统反应也存在限制：系统必须在扰动信号所涉及的频率提供增益。如果设定点变化的扰动太快，励磁信号的频率成分就低于系统带宽，表示这些频率缺少增益：系统变慢且不会作出反应，工作状态就像环路对波形变化没有响应。那么，是否就要求无限大的带宽呢？不是的，因为增加带宽就象是拓宽漏斗的直径：您当然可以收集到更多信息，并对输入振动更快地作出反应，但系统也将接收到伪信号(spurious signal)，如转换器在某些情况下自己产生的噪声及寄生参数(如开关电源中的输出涟波)。因此，强制要求将带宽限制在您应用真正要求的范围。采用的带宽太宽将削弱系统的抗噪声性能(如其抑制外部寄生信号的强固性)。

限制带宽

我们怎样限制控制系统的带宽？方法就是通过补偿器区块G改变环路增益曲线。此区块将确保在一定量的频率fc后，环路增益的大小|T(fc)|下降至低于1或0 dB。如同我们所阐述的，一旦环路闭合，它大致就是您的控制系统的带宽。发生此现象时的频率称作交越频率，标作fc。这就是否足够获得强健的系统？不是的，我们需要确保另一个重要参数：幅值为1的点的相位T(s)必须低于-180°。从我们的实验来看，我们已经看到当环路增益在交越频率处低于-180°时，我们获得了朝稳态收敛的响应。这很明显是我们控制系统极想要的一种特征。为了确保我们在交越时避开-180°，补偿器G(s)必须在选定的交越频率处订制环路幅角(argument)以构建相位余量(phase margin, PM或φm)。相位余量可以被视作一项设计或安全限制，确保在即使存在外部扰动或不可避免的生产差异范围(production spread)的情况下，环路增益的变化不会破坏稳定性。我们在后文会看到，相位余量还会影响系统的瞬时响应。因此，相位余量的选择并不只是取决于稳定性考虑因素，还取决于您期望的瞬时响应类型。相位余量的数学定义如下所示：

其中T代表开环路增益，其中包括分级的控体H和补偿器G增益。

图3中显示了经典补偿的典型环路增益曲线，其中显示交越频率为6.5 kHz。在此点，T(s)相位为-90°。如果您想在6.5 kHz时从-180°起步，并正向清点相位度数直至穿越幅角波形，您在此例中就得到90°的相位余量。这就是一个极为强健的系统，被认为在各种条件下都稳定：即使在交越点附近环路增益有一定程度的变化，也没有可能在相位余量太小的频率交越。所谓的“太小”，我们指的是相位余量接近30°极限，低于此值时系统就提供不可接受的振铃(ringing)响应。这就是为什么您在上学时学习到45°是极限，此值相较于30°而言提供了额外的余量。我们稍后会看到这些数字的来源分析。

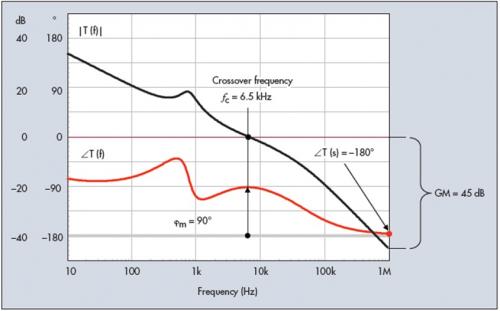
图3. 在此示例中，0 dB交越点位于6.5 kHz，此频率时总相位滞后提供了90°的相位余量

增益余量及稳定条件

图4显示了被补偿转换器的另一个典型频率响应，重点显示了0 dB交越点及相位余量。我们根据经验可知，构成转换器的元件在产生生命周期内会再现性能变化。这些变化可能是因正常的生产差异范围引起的(如电阻或电容遭受逐批次公差不同的影响)。转换器的环境工作条件也对元件有影响。在这些变量中，温度充当关键角色，影响被动或主动元件参数，如电容或电感等效串列电阻(ESR)、光耦电流传递比(CTR)或是双极晶体管的beta值。这些变量影响环路增益，使其上升或下降，具体则取决于受影响的参数。

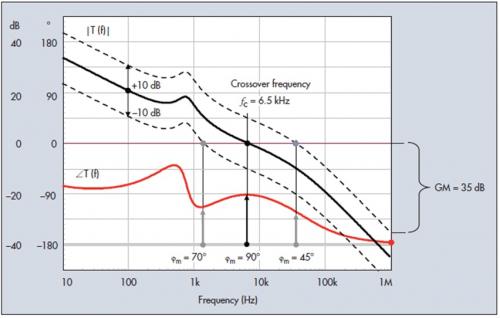
图4. 环路增益会显示出对温度等外部参数的敏感性。出现变化时，相位余量必须始终保持在安全限制范围内。

如果增益曲线出现变化，0 dB交越频率将过渡至新的值，为转换器施加不同的带宽。在这些变化条件下转换器的稳定性会受到怎样的影响？如果新的交越频率出现在相位余量较少的点，瞬时响应性能可能下降，使过冲不再能被接受。因此，身为设计人员，你的责任就是确保这些差量(dispersion)在你接近-180°极限时不会突然增大增益。您需要充足的增益余量，其定义如下所示：

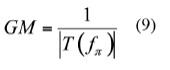
它对应于恰好为-180°或弧度的频率点(图3中为1 MHz).

图4描绘了由于所选择元件生产差异范围导致的±10 dB典型增益变化。它带来了1.5 kHz至30 kHz的交越频率。在此区域，相位余量从70°变为45°，这些都是理论上的安全数字。最坏情况是什么？就是新的交越频率在总相位滞后180°处出现。这条件在1 MHz时出来，表示有35 dB的正增益变化。

不太可能有大增益

有利的是，当今电子电路中不太可能出现35 dB的增益变化。以前，在变压器或伺服系统(servomechanism)采用真空管电路驱动的时候，上电序列期间的准备(warm-up)时间可能引起大的环路增益变化。因此，增益规定有必要排斥可能存在稳定性风险的第二个点。此总相位滞后达-180°的频率处的环路增益曲线上可见这增益余量，在图3中被标记为GM。在当今电子电路中，高于10 dB的增益余量通常就足够了，除非您的环路增益对外部参数极为敏感。

增益漂移的另一个示例如图5所示。图中显示另一个被补偿的转换器在10 kHz时出现80°的相位余量。根据前文的讨论，我们知道可能会出现增益变化，致使增益曲线上扬或下走。在我们的示例中，我们可以发现2 kHz附近一个区域的相位余量小到只有18°。如果出现20至25 dB的增益下降，你最后得到的控制系统就会出现相当危险的约2 kHz的低相位余量。这就会导致振荡响应，很可能超出过冲规范。此类系统被认为是有条件稳定。有利的是，如前所述，25 dB的增益变化并不常见，有这等增益余量的系统可被视为强健。然而，我看见过在一些设计案例中，最终使用者(您的客户)在规范中清晰标明不接受有条件的设计，要求在低于交越频率的所有点提供大于60°的相位余量。在这种情况下，就强制要求补偿转换器，使得无论什么工作条件下，低于交越频率时都不存在相位余量降低的区域。

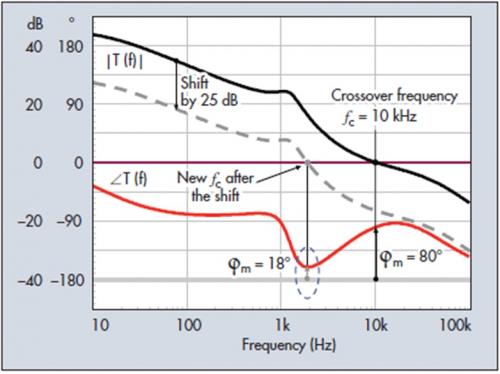
图5. 在此示例中，如果增益漂移至低于25 dB，曲线就在相位余量仅为18°的频率点过0 dB轴。如此的相位余量将受大的过问影响，提供振荡极大的响应。这就是有条件稳定的案例。

稳定，或是不稳定？

通常认为，在交越前相位下降至低于-180°的系统是不稳定的系统。这样的响应如图6所示。在1 kHz后相位曲线快速下降，并在1.5 kHz之后的数kHz范围内越过-180°的极限。然后相位曲线又上扬，在10 kHz时提供50°的相位余量。是的，此系统很稳定，只不过是因为在0 dB时我们不满足方程式(7)。要记住的是，要消除方程式(3)的分母，您必须使增益大小恰好等于1且相位滞后180°或更多。在图中，我们可以看到任何点都不满足此条件。然而，值得一提的是，此环路极具条件相关性。如果增益减少数dB，您的相位余量将变得低于45°。增益再下降10 dB，您将进入相位余量为0的危险区，这时会达到振荡条件。

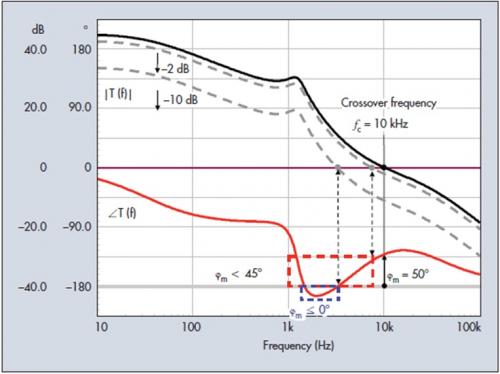
圖6. 相位滯後180°，但處於增益大於的區域。這並不構成問題，其回應可以接受。

节选自《线性及开关电源控制环路设计教程》(c) 2012一书。此书的主题包括：环路控制基础、传递函数、控制系统的稳定条件、补偿、以运算放大器为基础的补偿、以运算跨导放大器为基础的补偿、以TL431为基础的补偿、以为流稳压器为基础的补偿 、测量及设计实例。此书可以ArtechHouse.com、Amazon.com或BN.com上购买。