摘要
空间矢量脉宽调制(SVPWM)广泛用于3相逆变器控制系统。SVPWM MCU实现的最有效方法是中心对齐PWM,因为MCU中的PWM模块可轻松产生中心对齐PWM。本文将讨论SVPWM实现方法,并介绍一种轻松实现中心对齐SVPWM的方法,其适合于片上PWM模块。
1 引言
SVPWM广泛用于3相逆变器控制系统,原因是它比正弦脉宽调制(SPWM)拥有更高的DC侧电压利用效率。尽管SVPWM具有许多优势,但是它难以实现。最难的因素是计算每个功率开关的占空比,以及确定每个开关周期的矢量扇区和脉冲序列。许多文章都介绍了3相2级逆变器的占空比计算方法,并且我们可以使用许多方法来计算出矢量序列(例如,中心对齐方法,它可以在MCU平台中轻松地实现)。
为了改善3相逆变器的系统效率,3级或者多级逆变器正变得越来越流行。相比2级逆变器,3级逆变器拥有更多的功率开关(最多可达12个);这就意味着,3级逆变器比2级逆变器拥有更多的矢量扇区。因此,相比2级逆变器,3级逆变器SVPWM的占空比计算和矢量计算更加复杂。
本文[1]介绍了一种计算矢量扇区的简单方法。计算过程总共只有2步,第1步把整个矢量分为6个主要扇区。这一步与2级逆变器的扇区计算方法非常类似。第2步,把基准扇区重新定位至这6个扇区之一中,然后把这个主扇区分为6个子扇区。这种计算方法可用于2级逆变器,用于确定有效矢量和计算其停顿时间。但是,我们还没有讨论每个开关周期的矢量序列,并且占空比计算方法很难在MCU应用中实现。本文[2]把相同方法用于计算矢量。重新定位的零矢量作为2级逆变器的零矢量,则得到的矢量序列与2级逆变器一样。在实现过程中,MCU用于产生序列信号,并把外围逻辑电路用于每个功率开关的已实现PWM生成。我们并未介绍没有外围逻辑电路且适合于MCU实现的方法。
SVPWM MCU实现的最有效方法是中心对齐PWM,因为MCU的PWM模块可轻松地产生中心对齐PWM。本文将基于[1]和[2]所述方法,讨论SVPWM实现,并介绍实现中心对齐SVPWM的一种简单方法,其适合于片上PWM模块。
2 3相3级逆变器的基本SVPWM原理
图1显示了中点箝位(NPC)型3相3级逆变器的硬件拓扑。
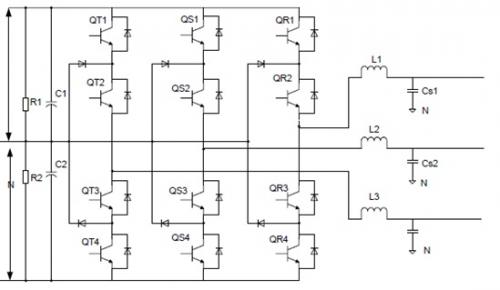
图1 NPC 3相3级逆变器的硬件拓扑
图1中,共有3个NPC腿(R、S和T);每个腿包括4个功率开关。每个腿的4个功率开关必须在两个补偿对中得到控制。Qx1、Qx3(x = R,S,T)为一个补偿对,Qx2、Qx4为另一对。因此,对于每个腿而言,它可通过4个功率开关输出3个不同相位的电压状态。
表1 每个腿的输出状态

当控制每个腿的功率开关(参见表1)时共有27个状态;每个状态均可映射到α- β坐标平面矢量图。27个矢量可形成18个扇区,如图2所示。

图2 3相3级逆变器SVPWM矢量图
假设基准矢量Vref。根据SVPWM理论,我们必须在图2中找出两个最接近的矢量Vx、Vy以及一个零矢量Vz,以组成矢量Vref。图2显示了Vref和Vx、Vy、Vz之间的关系。因此,我们可以选择矢量PNN(Vx)、PNN(Vy)和NNN(Vz),形成Vref。如果规定间隔Ts内Vx、Vy、Vz的停顿时间分别为Tx、Ty、Tz,则可得到如下函数:

但是,仅仅通过2级SVPWM中使用的角度还很难确定Vx、Vy、Vz,因为即使角度相同,但基准矢量可位于不同扇区内。为了确定该扇区,需要基准矢量的大小,但它会增加计算方法的复杂度。
[1]和[2]介绍了一种计算Vx、Vy、Vz的简单方法。首先,图2所示整个矢量图被分为6个主扇区。每个主扇区包含10个原始扇区,其会形成一个子六边形。这6个主扇区呈60度角差连续分布。图3显示了这6个主扇区。
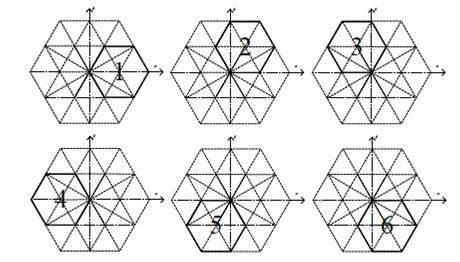
图3 3级SVPWM的主扇区
给定基准矢量Vref情况下,可仅利用该角度计算主扇区。例如,图4中,Vref和α轴之间角度θ为+60度到-60度,其意味着Vref主扇区为扇区1。
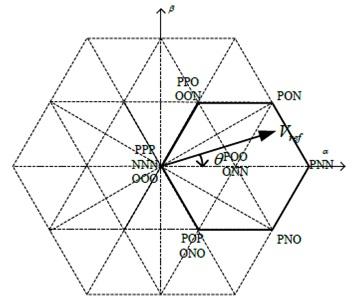
图4 主扇区1
在计算出主扇区以后,它必须把初始矢量映射到所选主扇区内。映射算法如下:

例如,主扇区1的初始矢量为PPP(OOO,NNN)、POP(NON)、PNO、PNN、PON、PPO(OON)、POO(ONN)。为了获得类似于2级SVPWM的六边形,把POO(ONN)作为映射矢量Vmap1=V0。在映射以后,我们可得到图5所示六边形,其与2级SVPWM的矢量图一样。在该六边形中,共有7个映射矢量,其在六边形中形成6个子扇区。
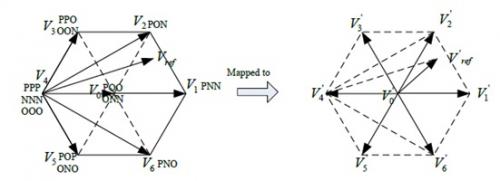
图5 主扇区1映射
由图5,我们可以看到,Vref位于子扇区1中,并且我们可以轻松地计算停顿矢量为V1和V2。V0可以作为2级SVPWM的零矢量。因此,我们可以得到如下函数:
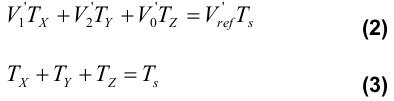
组合方程式(2)和方程式(3),得到:
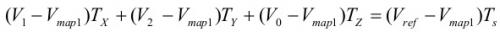
因此
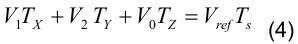
由方程式4,如果可以计算出停顿时间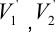 和
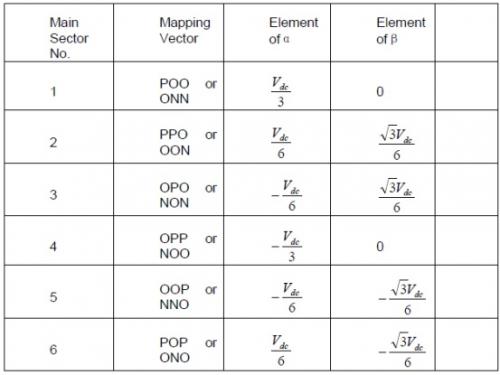
和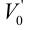 ,则可计算得到初始矢量停顿时间。由图5映射,3级SVPWM的矢量选择和停顿时间计算被完全转换为2级SVPWM。不同主扇区拥有不同映射矢量。表2总结了每个主扇区的映射矢量。
,则可计算得到初始矢量停顿时间。由图5映射,3级SVPWM的矢量选择和停顿时间计算被完全转换为2级SVPWM。不同主扇区拥有不同映射矢量。表2总结了每个主扇区的映射矢量。
表2 每个主扇区的映射矢量
3 主扇区计算简单方法
利用α- β坐标平面Vref角度,可计算出该主扇区。如图2和图3所示,每个主扇区均位于固定角度范围内。例如,第一个主扇区的角度范围为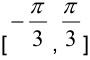 。还可以计算第二个主扇区的角度范围,其为
。还可以计算第二个主扇区的角度范围,其为 。因此,第一个和第二个主扇区之间的重叠区域,会延伸到两个相邻区域。这些重叠区域增加了主扇区的计算难度。为了规定每个扇区的独占角度区域,我们可重新定义主扇区,如图6所示。
。因此,第一个和第二个主扇区之间的重叠区域,会延伸到两个相邻区域。这些重叠区域增加了主扇区的计算难度。为了规定每个扇区的独占角度区域,我们可重新定义主扇区,如图6所示。

图6 主扇区新定义
利用图6所示定义,每个主扇区都有其自己的角度区域及其自己的子扇区。
鉴于图7所示3相电压波形,相应主扇区被标记在正确位置。由图7,表3总结了主扇区编号与3个相位元素之间的关系,其可帮助轻松确定主扇区。

图7 主扇区位置
表3 主扇区确定方法
