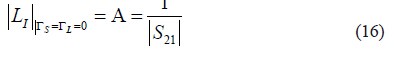1. 引言

辐射骚扰的测试数据反映的是电场或者磁场的强度。它通过天线检测，并在50 欧姆的同轴系统中被转换成传输信号。该信号通过同轴线缆和负载传输到测量接收机。传输路径的特征常用散射参数（S参数）表征。在本文中，被测信号和通过测量接收机记录的信号之间的传输因子F忽略了反射（失配）效应。这些因子经常在EMC 测试中用到。然而这种简化带来了误差，而这种误差是可以被用来做修正的。针对此误差，“失配“这个词符合参考文献[1] 中的定义δM。理所当然，测试结果和接收机记录的结果之间的关系应该是传输因子F 和失配误差的乘积（F*δM）或者是他们之和（F+δM）这取决于采用的单位标准（线性或者dB）。

2. 天线因子

辐射骚扰测试的电场或磁场强度的大小（|E| 或者|H|）是通过位于远区场的天

线检测得到的[2]。被测量值可以概括如下：

天线的两个因素，即天线因子FA 和负载端的反射系数ГS。而在校准过程中ГS 的计算是在和阻抗ZS 匹配的情况下进行的因此。只有天线因子的大小是测量的，因此FA 是关于频率的实变量。

天线因子FA 是天线处的场强和天线负载端电压|U| 的比值，该比值假定测试时天线馈电点无反射（ГS=0）。

图1 天线校准及等效电路图

如图1 所示的天线等效电路中的电动势|ε| 是与场强成正比。它适用于电场天线和磁场天线。

设定等效电路配备50 欧的负载，如图1 所示。使用校准公式和公式2，这样可以计算天线因子FA

在测试仪器是可追溯性校准并且失配是可以补偿的情况下，忽略反射系数，即公式3 中的ГS=0 是合理的。但是接收机输入端的反射总是存在的，它对于骚扰测试的测试路径适配误差是有贡献的。

3. 天线接收机直接连接的失配误差

如果天线直接与测试接收机连接，则接收机输入端的电压降U 可按下面的公式计算：

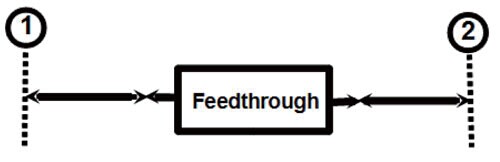
图2 在辐射骚扰测试的天线和接收机之间插入传输路径

联立公式3 和公式4，可得：

考虑接收机输入端的失配问题（公式14），可得：

可以看出：

它是在直接连接天线和接收机时的辐射骚扰测试失配误差。

4. 天线与接收机通过插入路径连接的失配误差

通常情况下，天线与接收机是通过两根同轴线缆组成的路径相连接，通常安装在测试屋的墙壁上，如图2所示。测试情形如图7b 所示，天线作为源头，负载是接收机，在端口1 和2 之间的插入路径用S 参数矩阵来表征。设置插入损耗如公式15，接收机输入端电压降按照直接连接天线的公式5，此后对电压降U2 运用接收机失配公式14，这样得到|Q| 和电压|U2| 之间的关系：

天线插入路径的重计算因子是天线因子和路径衰减的乘积：

是辐射骚扰测试中天线通过插入路径连接接收机的失配误差。

5. 天线和接收机反射的思考

天线馈电点的反射系数ГS 分别出现在没有插入路径和具有插入路径的情况下计算出的失配误差中，如公式7 和公式10 所示。

电子天线校准是在全波暗室即无反射暗室中进行的。在全波暗室中进行辐射骚扰测试具有相同的电磁环境。因此在该环境中的ГS 是确定的复变量，独立于天线距地面距离和天线极化方向。

可是，在半波暗室中进行辐射骚扰测试时，天线的高度是变化的，而且天线极化方向和角度也是变化的，因此反射系数ГS 是一个变量，与之前提到的天线高度、角度和极化方向有关。严格来讲，应该得到反射系数ГS 关于天线高度、极化方向和角度的极值，这样为反射系数ГS 作为一个随机变量确定了变化范围。幸运的是，这个变化很微小，因此本文中ГS 定义为一个确定性的变量，依赖于典型的天线高度以及独立的水平极化和垂直极化方向。

另一个简化的地方是由于远场条件测试，反射系数ГS 几乎独立于被测试设备（EUT）。因此，EUT 对反射系数ГS 的影响可以忽略。

天线馈电点的反射系数ГS 不会在用磁场天线进行测试时发生变化，因为天线的校准和测试是在同一个环境中进行的，即在半波暗室中是在距地面固定高度，且只有一个极化方向时进行。

在接收机输入端测量复反射系数ГL 是可能的，但是费用很高。信号的替代源可以是技术规范的接收机。通常情况下，两个极值是可以得到的，即|ГL| 的极值可以在接收机输入端的衰减器打开和关断状态下得到。为了保持好的信噪比和控制噪声电平与极限标准有较大的距离，通常是在接收机的输入衰减器关闭的情况下进行辐射测试的。如果接收机前端的前置放大器可用，那么用它来提高这两项性能。

6. 失配误差的估计

在文献[1] 中介绍的方法使用的失配误差为dB 形式，（公式10），log 的功能是所有组成部分的数学总和。

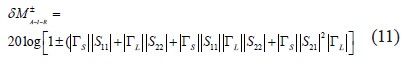
另外，公式11 构造了具有U 形概率分布的10 维随机变量（5 个复随机变量）的变化的边界范围。所以变量a 的一半的变化范围和期望值E 可由以下公式得到：

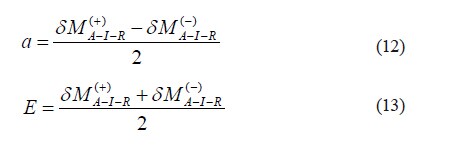
由于具有U 形的概率分布，因此采用了公式2 中a 的 倍与标准不确定性u 的比。严格来说，这个分布不是很有效。

事实上，公式10 中的失配误差是一个二维随机变量而只有复反射系数|ГL| 是随机的。合适且有效的估计误差的方法是应用蒙特卡洛方法[3,6,7]。与作者之前的文章相似[4]，他使用了Mathcad13 软件中的具有同一概率分布的伪随机数发生器。计算得出期望值E（X）作为算术平均，标准不确定度 u 为

7. 传播分布参数的微积分

路径的散射参数是通过利用R&S 公司的ZVRE 矢量网络分析仪针对30MHz 到1GHz 的频段内801 个对数分布的频点的测量得到的。HP 公司的85032B N 型套件用来进行校准。

该测试使用R&S 公司的ESIB40 型号接收机为测试装置。根据手册，0dB 衰减时，接收机输入端的电压驻波比不能大于2.0。此外，当输入衰减至少为10dB 时，在20Hz 到40GHz 的全频段，电压驻波比不能大于1.2。换算到反射系数上，这意味着0dB 的输入衰减时的反射系数|ГL|<0.34。考虑这个数值是因为之前介绍的在辐射发射中，接收机输入端的衰减器是关闭的。这样在0到0.34 间将产生180 个均匀分布的随机反射系数|ГL|值，每一次在区间 [-π : π] 中，它们都伴随着180 个随机反射系数|ГL| 的参数。

在半波暗室中，测试路径由9 米的同轴线缆，馈通组成。路径的散射参数见图3。

考虑EMCO3141 型宽带BiLog 天线。天线馈电点的反射系数ГS 是在空的半波暗室中测量的。分别采取天线距离地面1.5 米和1.7 米，水平和垂直极化的方式进行测量。反射系数ГS 和频率的关系如图4 所示。只能观察到滑坡型的差异。

在垂直极化和水平极化方向下的CISPR 方法和蒙特卡洛近似方法的结果比较如图5 和图6 所示。在C 频段（30MHz-300MHz）和D 频段（300MHz-1GHz）的极值标准不确定性列举在表1 和表2 中。

图3 插入路径的S参数

图4 天线馈电端的反射系数|ГL|，分别采取天线距离地面1.5米和1.7米，水平和垂直极化的方式进行测量

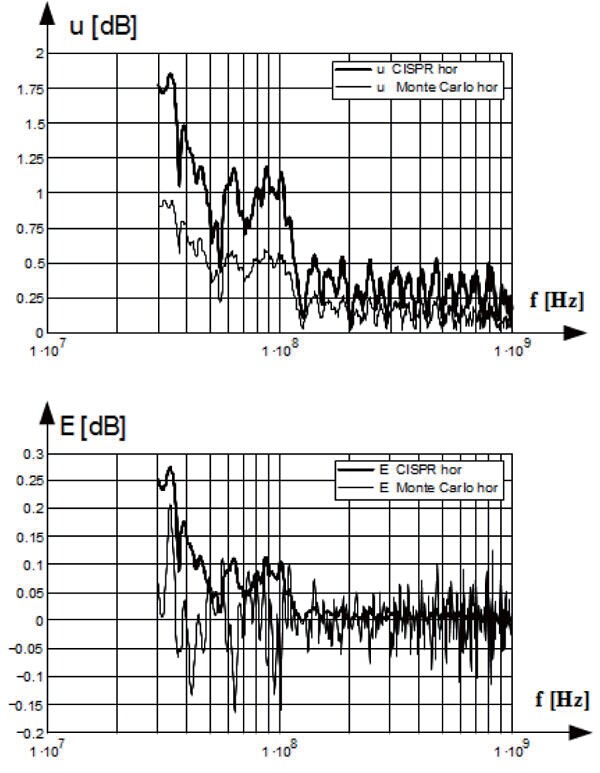
图5 天线水平极化方向下失配误差的标准不确定度u和期望值E

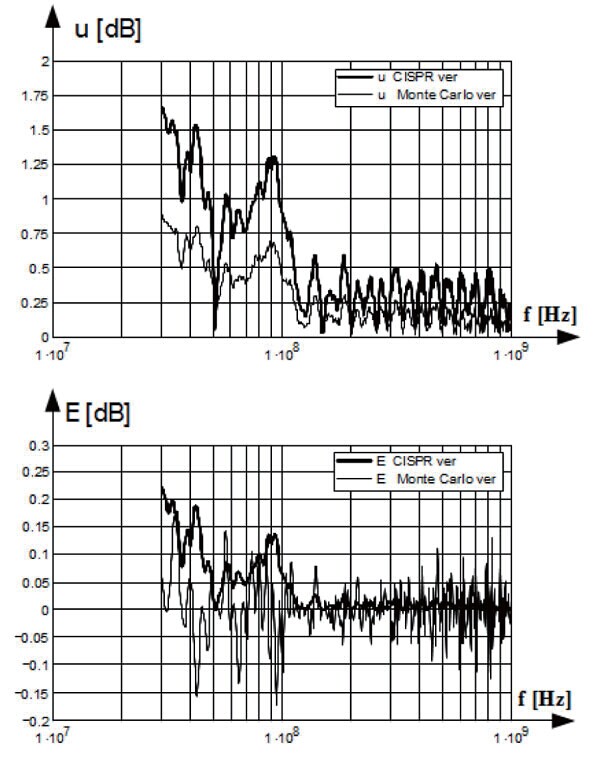
图6 天线垂直极化方向下失配误差的标准不确定度u和期望值E

8. 结论

根据文献[1] 中辐射发射测试的的失配误差δ MA I R ? ? （公式10）是一个具有近似U 型概率分布的十维随机变量。利用公式11 可以估计它的变化范围。计算这样分布的参数如期望值和标准不确定度是很简单的。在半波暗室中进行的电子骚扰测试中。如果天线馈电端的反射系数ГS 被认为与天线的水平垂直极化方式独立，则ГS 是一个确定的值。

在这样的情形下，由于接收机输入端的随机复反射系数ГL 的关系，失配误差的计算公式10 就成为了二维随机变量。这样，蒙特卡洛方法就能很轻松的解决这种问题。

本文中使用同一个实例，用上述两种方法计算。两种方法计算得到的期望值是微不足道的。在关心的D 频段（300MHz-1GHz），利用CISPR 方法计算的标准不确

定度被过分和不必要的放大了。

在C 频段（30MHz-300MHz），计算得到较大的天线馈电端的反射系数ГS 和具有较大极值的接收机输入端的反射系数ГL 是具有巧合性的。因此在C 频段比D频段具有更大不确定性。

9. 附录

9.1 接收机失配

如果考虑测量接收机输入端的反射ГL，而且信号由接收机寄存和显示，那么电压UR 和接收机输入端的U 不同，它们的关系如下式所示：

9.2 插入损耗LI

插入损耗LI 是电压U 和U2 的比值，其中U 是在源和负载直接相连的情况下，源和负载连接处的电压（如图7a 所示），而U2 是当一个二端口网络插入到源和负载之间时的负载两端的电压（如图7b 所示）。

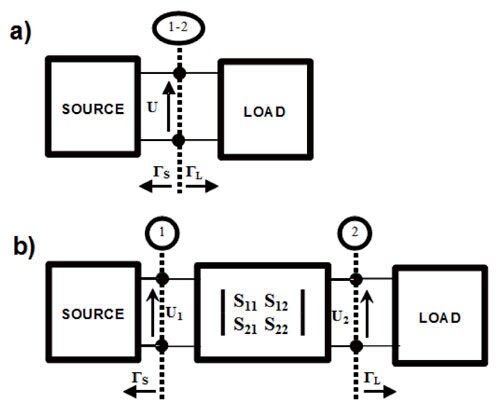
图7 插入损耗公式中定义的符号的图示

当具有几乎无反射的源（ГS=0）和负载（ГL=0）的情况下，插入损耗是传输参数S21 的倒数。它的大小被称作衰减系数