1. 引言
Langer EMV-Technik 在抑制电路板电磁干扰领域有20 年的工作经历。通过解决大量的实际问题,我们在高频场的测试方面积累了大量的经验。利用这项技术,出现了大量的近场探头,这些探头给实际集成项目的测试带来很多益处。
在电磁兼容领域,近场探头有很好的用处,比如在小规模的设备中发现噪声发射源,开关转换器的近场测量和检测整个集成设备的最高发射频率。
可是由于场强是耦合成传感器的输出电压,在实际物理环境中,测量的结果通常不被采用。此外,这个输出电压还依赖于探头的频率响应,而这个频率响应是频率的函数。由于以上对测量技术的限制,只能通过比较测量来解决实际问题。可是在早期阶段,是通过建立对干扰场强的确切分布的认知来抑制电磁干扰问题的。也经常利用比较测量中的绝对值测量来解决问题。此外,自动化研发人员的焦点更多的处在物理机理上,这也将引领更快速地来解决问题。
2. 建立磁场校正
与近场探头相关的物理因素是基于电磁感应定律的。它表述为在一个导体环上的变化的磁场将产生相应的电压。普遍的数学表达是:
∮ _da ? 〖 Ed = N ? _A ? ? B / ? t 〗 dA ( 1)
从技术层面上说, 表达式可以简述为:等式的左边可以用导体环的电压U_induziert 来代替。此外右边的面积分可以用线圈的面积A 来代替。
导体环的感应电压是对磁通密度的变化率的测量。
U_induktion = - N ? B / ? t A
B :磁通密度
t :时间
A :线圈面积
N :匝数 ( 2)
可是,这种简化只是在不考虑环的场分布时可行,此时整个线圈表面磁通密度是均匀的。
通过改变可视范围,可以获得一个关于频率的线性函数,这个函数给出了磁场强度和感应电压的直接关系。
U_indiziert = ωBAN = μωHAN
其中 B = μ? h( 空气中) (3)
高频测量技术通常在50 欧姆的系统中运行。这个低负载阻抗区别于感应电压的探头输出电压。通常用探头转移函数来描述这时的误差。
U_out = G_Sonde ? U_induziert (4)
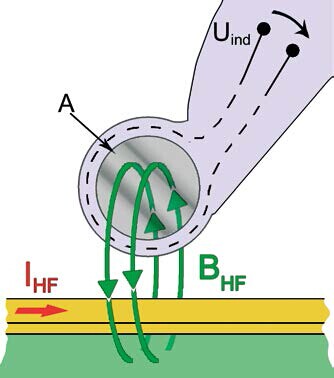
图1 探头结构概念图
探头的转移函数是特定的并且通过测量确定。
磁场校正因子通过传感器输出电压和引发的磁场来调整。
H / U_out = K_H ( ω ) = G_Sonde 1/μANω [A / Vm ] (5)
3. 基于MFA K0 0.1 to 30 探头确定校正曲线
在这个例子中我们使用新的MFA K0.1-30 探头。这个探头用来测量非常小结构设备的磁场和电流,但需要人工测量。测试探头针对周围的场经过特殊设计以便带
来强的抑制。这样,测试可以在公共环境中进行。指标是采取0.2mm 间距以及最高频率是1GHz。
利用探头测量高频带状线是确定修正曲线的起始点,这样将产生一个固定频率的磁场。利用这个磁场,可以确定探头G_(SL 探头)的传输特性。
U_out = / U_quelle
探头的传递函数的传递特性是利用一种特殊的数学方法计算的。然后,磁场修正曲线根据公式5 和探头参数确定。
下图描述了如何建立修正曲线。
.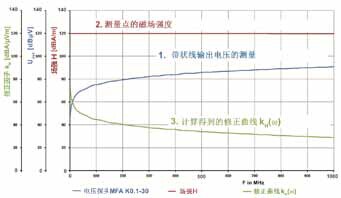
图2 修正曲线的建立
4.规范测量磁场强度
模块特定区域和信号导线的磁场强度的测量和校正因子的测定相似。
转移探头到测试点然后测量传感器输出电压。然后,使用校正因子的的电压将在幅度值和单位上发生变化。校正的结果便是磁场强度的测量值。
下面的公式是为测量值的进行特定修正,公式使用的是方程5 的对数方程。
H [dB A / m] = U_out [dBuV ] + K_H [ dB A / (μVm )] (6)
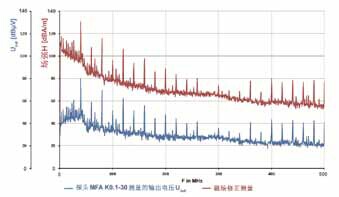
图3 自旋供电电路测试的测量值和修正值
图3 描述了自旋供电电路的频率响应(蓝色)。在开关电路运行的频率上检测周期循环时钟频率峰值。红色的频率响应描述了频率响应曲线的偏移校正。在这个图中,可以得到供电回路中感生电流产生的射频磁场强度。
位于环路上的其他模块的计算可以使用公式3。
实际中有很多不同的校正因子,比如测试导线中的电流。可是,这些因子只有在满足测量安排的要求下有效。