现代导航对系统有能够实时、准确地获取载体运动信息的要求。在组合导航领域,卫星导航(目前最常用的是GPS)与捷联式惯性导航(SINS)组合的导航系统能够弥补各自单独导航情况下的不足,而且具有高精度、低成本、结构简单等优点,目前已经成为最热门的研究方向。GPS/SINS组合导航一般是以位置,速度作为量测量来修正惯性导航系统,随着GPS定向系统的逐渐发展,将姿态与位置和速度同样作为量测量的全组合方法正在成为研究热点。本文根据GPS/SINS全组合导航系统的机理和特点在基于DSP+FPGA的导航计算机平台上设计了可靠的信息融合技术,通过相关的试验证明本系统具有较好的效果。
组合导航系统软硬件设计
导航计算机总体设计
捷联式惯性导航系统中将陀螺仪、加速度计、电子线路和金属台体合称为惯性测量装置(IMU),它是整个系统的核心部件。本文中导航系统采用方便野外跑车实验的一体化、模块化设计,通过接口将导航计算机固连于IMU器件内,计算机与IMU方便更换。本系统中设置IMU数据更新率为200Hz,GPS数据输出频率为1Hz,因此计算机必须能够在5ms内完成整个系统算法运行,这样的速率要求使得单纯采用一个核心处理器的方法已无法满足系统实时性要求,故本系统中计算机采用了DSP+FPGA双核设计方式,DSP选用TI公司的TMS320C6747,TMS320C6747具有高性能的浮点运算能力,最高主频可达到450MHz,能够实现高速运算;而FPGA型号为Xilinx公司的XC3S500E。系统硬件结构如图1所示,其中,DSP6747主要负责IMU解算、卡尔曼滤波等数据处理算法,FPGA主要完成外部接口扩展(2路RS232口,1路RS422口)、数据的采集与传输及逻辑时序控制的功能。
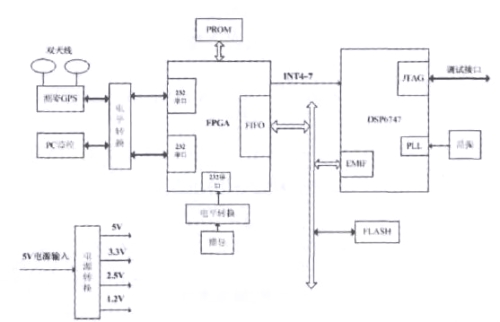
图1 导航计算机结构图
导航系统软件设计
导航计算机软件设计必须满足实时性与准确性的要求。计算机上电后会执行整个系统的初始化,通过后开始捷联惯导算法运算,组合导航算法在GPS数据获取后将其作为初始数据进行运算,如果有GPS数据丢失状况发生,系统将单独运行捷联惯导解算,经解算后的数据被送入Kalman滤波器中处理。系统软件流程图如图2所示。
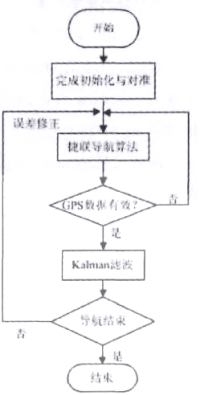
图2 系统软件流程图
组合导航系统算法
(1)组合导航的状态方程
目前,GPS/SINS组合导航方式主要分为松散组合和紧密组合。而松散组合大多采用位置、速度组合模式,而本文中加入双天线GPS姿态角作为量测量进而实现全组合方式。其状态方程如公式(1)所示:
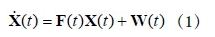
其中F(t)是18*18阶的状态转移矩阵;W(t)为18维的状态噪声向量;下列各式给出了状态方程的系统噪声性质:
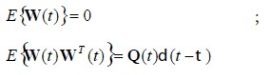
系统状态X(t)选取为:
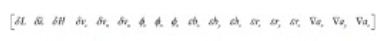
其中δL、δλ、δH为经度、纬度、高度误差,δVe、δVn、δVu分别为
东北天三个方向上的速度误差,Φe、Φn、Φu为平台误差角,εbx、εby、εbz,εrx、εry、εrz,Δax、Δay、Δaz分别为陀螺常值漂移,相关漂移与加速度计的零偏。
而其中失准角误差方程为:
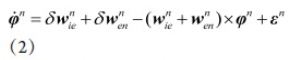
速度误差方程为:
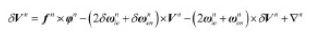
位置误差方程为:
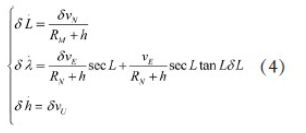
(2)组合导航系统的量测方程
由于系统将定向GPS给出的数据作为修正数据,系统量测值在位置和速度值的基础上加入了姿态信息。位置量测值为惯导系统与GPS给出的纬度、经度和高度差,相应的速度量测值为惯导系统与GPS给出的在惯性系统中各坐标下的差值,而惯导系统与双天线GPS给出的姿态差值作为第三组量测值。
惯导系统与GPS位置量测信息在地理坐标系以真值和误差表示如下:
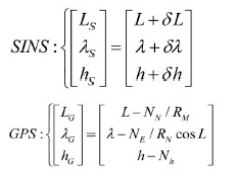
式中L、λ、h表示运载体真实位置,Ne、Nn、NH为GPS东北天方向位置误差。
位置量测方程如下:
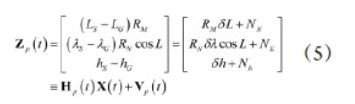
与位置量测方程形式相似,速度量测方程表示如下:
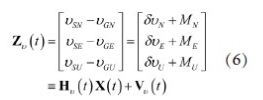
下式为姿态量测方程:
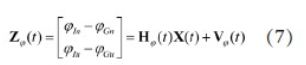
将(2)(3)(4)式组合后可以得到整个系统的量测方程如下
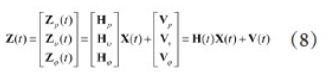
本文采用卡尔曼滤波算法对GPS,IMU数据进行融合。将式(1)(8)离散化后方程为:
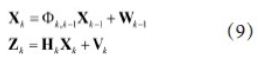
一步预测状态方程为:

状态估计方程为:

滤波增益为:
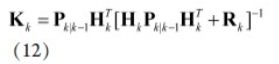
计算得到一步预测均方差:
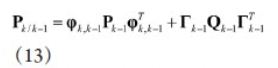
则均方差误差估计:
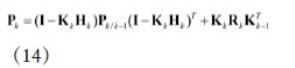
试验结果
为了验证本文提出的双天线GPS/SINS组合导航系统的可行性,在南京某地进行了跑车实验。其中姿态GPS模块定位精度小于5m,速度精度0.1m/s,航向精度0.1°。IMU常值漂移小于0.1°/h。跑车过程中以高精度GPS作为真实值,将组合导航系统输出值与高精度GPS数据进行比较。整个系统中每5ms进行一次惯导数据解算,通过卡尔曼滤波算法进行数据修正的频率为1次/s。将跑车过程中导航计算机输出数据存入文件,通过MATLAB进行数据处理。图3中给出一次跑车中组合导航系统与高精度GPS同一时刻输出数据的差值,结果如图3所示。
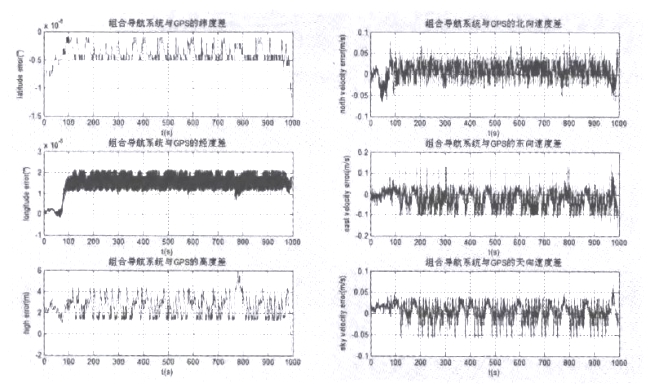
图3 组合导航与GPS误差曲线
从图3可以看出,在动态情况下本文提出的组合导航系统具有较高的定位精度,从与高精度GPS数据对比中可以看,此系统定位误差在4m以内,而速度误差在0.1m/s左右,达到了系统的要求,充分满足了实际应用需求。