1引言

CPLD(ComplexprogrammableLogicDevice，复杂可编程逻辑器件)和FPGA(FieldprogrammableGatesArray，现场可编程门阵列)都是可编程逻辑器件，它们是在PAL、GAL等逻辑器件基础上发展起来的。同以往的PAL、GAL相比，FPGA/CPLD的规模比较大，适合于时序、组合等逻辑电路的应用。它可以替代几十甚至上百块通用IC芯片。这种芯片具有可编程和实现方案容易改动等特点。由于芯片内部硬件连接关系的描述可以存放在磁盘、ROM、PROM、或EPROM中，因而在可编程门阵列芯片及外围电路保持不动的情况下，换一块EPROM芯片，就能实现一种新的功能。它具有设计开发周期短、设计制造成本低、开发工具先进、标准产品无需测试、质量稳定以及实时在检验等优点，因此，可广泛应用于产品的原理设计和产品生产之中。几乎所有应用门阵列、PLD和中小规模通用数字集成电路的场合均可应用FPGA和CPLD器件。

在现代电子系统中，数字系统所占的比例越来越大。系统发展的越势是数字化和集成化，而CPLD/FPGA作为可编程ASIC(专用集成电路)器件，它将在数字逻辑系统中发挥越来越重要的作用。

在数字逻辑电路设计中，分频器是一种基本电路。通常用来对某个给定频率进行分频，以得到所需的频率。整数分频器的实现非常简单，可采用标准的计数器，也可以采用可编程逻辑器件设计实现。但在某些场合下，时钟源与所需的频率不成整数倍关系，此时可采用小数分频器进行分频。比如：分频系数为2.5、3.5、7.5等半整数分频器。笔者在模拟设计频率计脉冲信号时，就用了半整数分频器这样的电路。由于时钟源信号为50MHz，而电路中需要产生一个20MHz的时钟信号，其分频比为2.5，因此整数分频将不能胜任。为了解决这一问题，笔者利用VIDL硬件描述语言和原理图输入方式，通过MAX+plusII开发软件和ALTERA公司的FLEX系列EPF10K10LC84-4型FPGA方便地完成了半整数分频器电路的设计。

2小数分频的基本原理

小数分频的基本原理是采用脉冲吞吐计数器和锁相环技术先设计两个不同分频比的整数分频器，然后通过控制单位时间内两种分频比出现的不同次数来获得所需要的小数分频值。如设计一个分频系数为10.1的分频器时，可以将分频器设计成9次10分频，1次11分频，这样总的分频值为：

F=(9×10+1×11)/(9+1)=10.1

从这种实现方法的特点可以看出，由于分频器的分频值不断改变，因此分频后得到的信号抖动较大。当分频系数为N-0.5(N为整数)时，可控制扣除脉冲的时间，以使输出成为一个稳定的脉冲频率，而不是一次N分频，一次N-1分频。

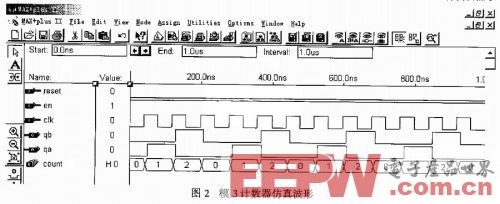
图2模3计数器仿真波形

3电路组成

分频系数为N-0.5的分频器电路可由一个异或门、一个模N计数器和一个二分频器组成。在实现时，模N计数器可设计成带预置的计数器，这样可以实现任意分频系数为N-0.5的分频器。图1给出了通用半整数分频器的电路组成。采用VHDL硬件描述语言，可实现任意模N的计数器(其工作频率可以达到160MHz以上)，并可产生模N逻辑电路。之后，用原理图输入方式将模N逻辑电路、异或门和D触发器连接起来，便可实现半整数(N-0.5)分频器以及(2N-1)的分频。

4半整数分频器设计

现通过设计一个分频系数为2.5的分频器给出用FPGA设计半整数分频器的一般方法。该2.5分频器由模3计数器、异或门和D触发器组成。

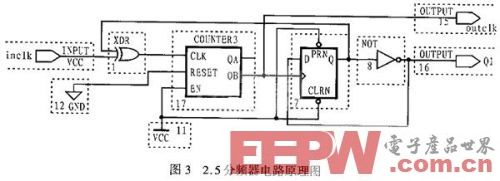
图3 2.5分频器电路原理图

4.1模3计数器

该计数器可产生一个分频系数为3的分频器，并产生一个默认的逻辑符号COUNTER3。其输入端口为RESET、EN和CLK;输出端口为QA和QB。下面给出模3计数器VHDL描述代码：

任意模数的计数器与模3计数器的描述结构完全相同，所不同的仅仅是计数器的状态数。上面的程序经编译、时序模拟后，在MAX+PLUSII可得到如图2所示的仿真波形。

4.2完整的电路及波形仿真

将COUNTER3、异或门和D触发器通过图3所示的电路逻辑连接关系，并用原理图输入方式调入图形编辑器，然后经逻辑综合即可得到如图4所示的仿真波形。由图中outclk与inclk的波形可以看出，outclk会在inclk每隔2.5个周期处产生一个上升沿，从而实现分频系数为2.5的分频器。设inclk为50MHz，则outclk为20MHz。因此可见，该电路不仅可得到分频系数为2.5的分频器(outclk)，而且还可得到分频系数为5的分频器(Q1)。

5结束语

选用ALTERA公司FLEX系列EPF10K10LC84-4型FPGA器件实现半整数分频后，经逻辑综合后的适配分析结果如表1所列。本例中的计数器为2位宽的位矢量，即分频系数为4以内的半整数值。若分频系数大于4，则需增大count的位宽。

表1半整数分频器适配分析结果