心电信号噪声的数字滤波研究-文章-技术应用-医疗电子

心电信号噪声的数字滤波研究

时间:07-02 16:31 阅读:1796次

*温馨提示：点击图片可以放大观看高清大图

简介：现代医学表明，心电信号（ECG）含有临床诊断心血管疾病的大量信息，ECG的检测与分析在临床诊断中具有重要价值，是了解心脏的功能与状况、辅助诊断心血管疾病、评估各种治疗方法有效性的重要手段[1]。但由于实际检测工况的非理想，ECG 信号中往往含有工频噪声及电极极化等引起的各种随机噪声 [2]。

现代医学表明，心电信号（ECG）含有临床诊断心血管疾病的大量信息，ECG的检测与分析在临床诊断中具有重要价值，是了解心脏的功能与状况、辅助诊断心血管疾病、评估各种治疗方法有效性的重要手段[1]。但由于实际检测工况的非理想，ECG 信号中往往含有工频噪声及电极极化等引起的各种随机噪声 [2]。噪声的存在降低了诊断的准确性，其中影响最大的是50Hz 工频干扰和基线漂移噪声。因此，在ECG 信号检测过程中，如何抑制工频干扰和基线漂移是必须解决的问题。

1. 数字滤波系统

心电信号是微弱低频人体生理电信号，通常频率在0.05~100Hz，幅值不超过4mv，通过安装在皮肤表面的电极来获取。由于人体是一个复杂的生命系统，存在50H 工频干扰及基线漂移等其他生理电信号的干扰。噪声可能会影响到医生的临床诊断，因此，需对心电信号进行滤波，即必须做好前端数据采集的软硬件设计以保证心电数据的可靠和准确。

传统医疗设备分别采用50Hz 带阻滤波器和RC 高通滤波器滤除工频干扰和基线漂移。但带阻滤波器电路复杂，其特性对元器件的精度敏感，而基线漂移本质上是一种缓慢变化的低频信号，采用RC 滤波器很难将高通滤波器的过渡带做得十分陡峭，基线漂移补偿效果不理想。因此，模拟方法往往不太容易获得很好的特性。

数字滤波方法有具有许多优点[3]，ECG 数字滤波系统组成如图1 所示，来自各电极的多路心电微弱信号经多路输入缓冲器缓冲放大，经导联选择电路进行选择后，由前置放大电路放大，进行电压放大以适应A/D 转换的幅度要求，然后进行数字滤波并输出心电信号。数字滤波用于心电信号消噪，不仅能提高仪器设备的性能，而且对于不同的使用环境(例如对于不同国家的50Hz 或60Hz 供电条件)，只需重新设置软件参数即可，大大降低了医疗设备硬件复杂程度，降低了产品成本、提高了通用性。

图1. 心电信号数据采集与处理框图

2．工频干扰滤波

对于心电信号中的工频干扰，简单而有效的方法是采用梳状滤波器滤波，这种FIR 滤波器简单、容易实现、滤波效果好，节数为N 的梳状滤波器的系统函数为：

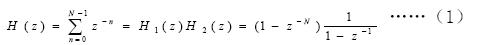
其中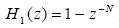，是由N 节延时单元组成的梳状滤波器，H1(z)的幅值响应由许多频率间隔相同的通带和阻带组成，它只许一些特定频率范围的信号通过而阻止另一些特定频率信号通过[4]。H(z)的频率响应为：

根据式(2)可知，梳状滤波器是具有线性相位的FIR 低通滤波器，相移τ=(N-1)/2，为使滤波器的直流增益为1，可以考虑在H(z)中增加增益因子1/N，归一化后的幅频响应为：

N=10 时，幅频响应如图2 所示，在频率点ωk=2πk/N，k=0,1,2,……N-1 处的幅值为0,因而在ωk=2πk/N 附近形成了多个阻带，对这些频率的信号具有很好的抑制作用。由于梳妆滤波器的系数相等且都为1，因而容易实现，常用于对医疗仪器中的特定信号进行滤波处理。

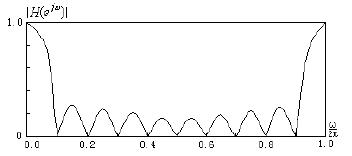
图2. 线性相位FIR 滤波器的幅频响应特性

根据图2 可得第一旁瓣峰值衰减约为20dB，若不能满足要求，可对式(1)进行修正：

其频率响应为：

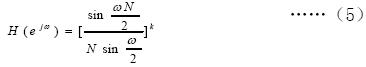
衰减速度为修正前的k 倍，k=2 时修正滤波器的幅频响应如图3 所示，其衰减性能更好。

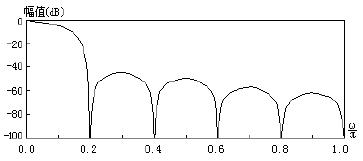
图3. 经修正以后的梳状滤波器幅频响应

3．基线漂移的抑制

抑制基线漂移方法很多，各有特点。基于抛物线的拟合基线算法结构复杂，采用单片机的嵌入式系统运算速度难以保证实时性要求[2]，基于小波的自适应滤波抑制ECG 基线漂移，运算较复杂，不适合用于小系统的监护。本文采用一种自适应快速线性拟合来抑制基线漂移的方法，通过多点采样，用最小二乘法拟合出基线的变化趋势，经修正得到ECG 信号。

3.1 QRS 波群的探测

理论上，两个连续QRS 波群之间的T-P 段代表了实际的ECG 基线水平。根据每一个心动周期的P-R 段特征点，在两个特征点之间进行插值，然后再进行曲线拟合，即将插值和曲线拟合结合起来，就可以得到基线漂移曲线，原始信号减去基线漂移曲线即为ECG 信号。因此，采用分析斜率、幅度和宽度的方法来识别QRS 波群[5]。根据ECG 的功率谱，QRS 波群的能量主要集中在15Hz 频率左右，为消除ECG中其它频率成分对QRS 波群检测的影响，需设计一个中心频率为15HZ 的带通滤波器，ECG 信号通过该滤波器时对R 波以外的频率成份进行了衰减。当采样频率为500Hz 时，该滤波器的传递函数如下：

由于R 波含有丰富的高频谐波成分，为突出高频谐波分量，采用如下微分器：

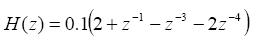
经处理后的信号通过带通滤波器和微分器后，P 波和T 波都有显著的衰减，相应的QRS 波群的峰值进一步加强，为消除微分器处理后散粒随机噪声产生的干扰，可以采用式（7）所表示的积分器进行修正：

然后，采用斜率跟踪法进行R 波识别，找出与QRS 波群检测特征点前后60ms相当的间期来识别R 波。当采集波形的斜率变化超过设定的阈值时，斜率变化最大处即为R 波所在的位置[5]。实验的采样时间为4.8 秒，采样点数为2048 个点。

许多异常的QRS 波群有高幅度和上升不迅速的特点，为提高以R 波斜率检测QRS 波群的可靠性，可采用移动窗口积分法验证以保证可靠检测。为便于进行积分运算，先将采样点进行逐点平方运算，并进行移动窗口积分，其差分方程如下：

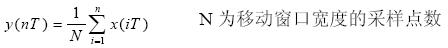
窗口宽度应当尽可能与QRS 波群宽度相近。若窗口太大，积分波形将把QRS 波群和T 波融合在一起，若窗口尺度太小，一个QRS 波群在输出中可能会产生几个峰值。

3.2 自适应线性拟合

在抑制基线漂移的算法中，须首先确定基线的变化趋势，为此应在两个心动周期中找到一段反映ECG 基线变化趋势的曲线。QRS 波群是心电信号的高频部分，其中R 波具有波形陡峭、幅度大、宽度窄、变化趋势明显等特点，因而以R 波为基准点寻找代表基线的时段。依次取每个检测的R 波峰值点作为参考基准点，利用回溯法求出每个TP 间期。确定了曲线区间就可采用自适应快速线性拟合法，拟合出基线的变化趋势。

采用最小二乘法计算各区间线性拟合的斜率和截距，拟合出基线的变化趋势。

对于观测点（xi , yi）i=1,2…n，若y 与x 具有线性模型，则任意一对观测值（xi , yi）存在如下关系：

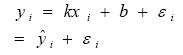
式中，εi 为理想状态i yˆ 和观测值yi 的误差，令：

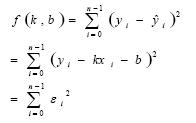
显然，f(k,b)越小，结果就越精确，因此根据最小二乘法可推导出[4]

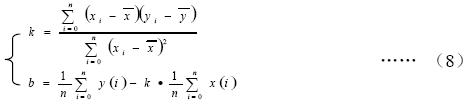
若斜率k>0 表示往上漂，k<0 往下漂，k=0 则没有漂移。根据分段修正所求出的k 值，判断基线的变化趋势，从而修正每段基线漂移值，得到真实稳定的ECG 信号。

4. 滤波效果

图4 表明，未经滤波的心电信号存在较大的工频噪声，若取采样频率500Hz，梳状滤波器节数N=10，经滤波后心电信号的干扰被基本滤除。图5 为ECG 信号频谱，滤波前ECG 信号存在较强的工频干扰，滤波后频谱中已经没有50Hz 成分。数字滤波对消除50Hz 工频及倍频干扰具有很好的效果。

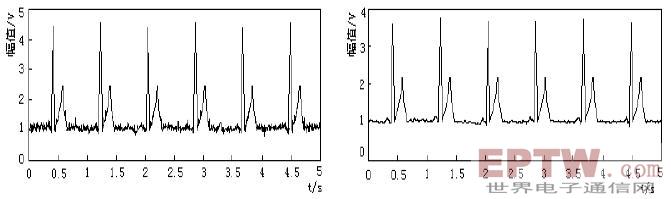
图4-1.含有工频噪声的心电信号图4-2. FIR 梳状滤波处理后的心电信号

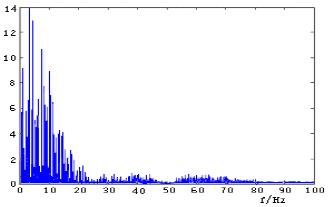
图5-1.滤波前ECG 频谱图5-2.滤波后ECG 频谱

图6-1 是存在基线漂移(上漂)的ECG 信号，采用自适应拟合算法抑制效果如图6-2 所示；图7-1 是存在下漂的ECG 信号，抑效果如图7-2 所示。实验表明，对于不同形式的基线漂移，该方法能很好的抑制ECG 信号基线漂移。与其他方法相比，自适应拟合算法简单、快速、易于实现、抑制效果好、信号失真度小。在嵌入式系统和对实时性要求较高的监护仪器中具有实际应用价值，也可用于其它信号检测仪器中。