FIR 滤波器广泛应用于数字信号处理中，主要功能就是将不感兴趣的信号滤除，留下有用信号。FIR滤波器是全零点结构，系统永远稳定；并且具有线性相位的特征，在有效频率范围内所有信号相位上不失真。在无线通信收发机中的DDC/DUC模块，抽取和内插都需要加入滤波器以防止信号在频谱上混叠，最典型的是采用 FIR滤波器实现半带滤波器。

FIR滤波处理如下式所示，其中x（n）为输入信号，h（n）为FIR滤波系数，y（n）为经过滤波后的信号；N表示FIR滤波器的抽头数，滤波器阶数为N-1。

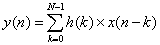
由上式可得到FIR滤波器在FPGA中的实现结构，如图1所示，主要由延迟单元Z-1、乘法器和累加器组成。此结构为直接型FIR滤波器结构，也称横向结构（transverse）。

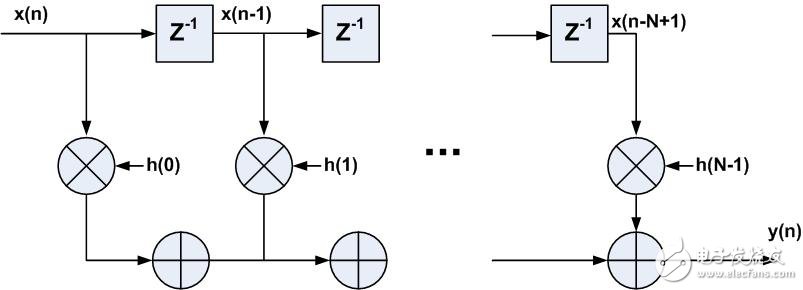
图1

设计FIR滤波器的方法有多种，其中Matlab软件提供了很多关于滤波器设计的工具箱，FDATool就是一个很好的工具，如图2所示就是FDATool的界面，可以在Matlab的Command窗口中直接输入FDATool命令来调用。

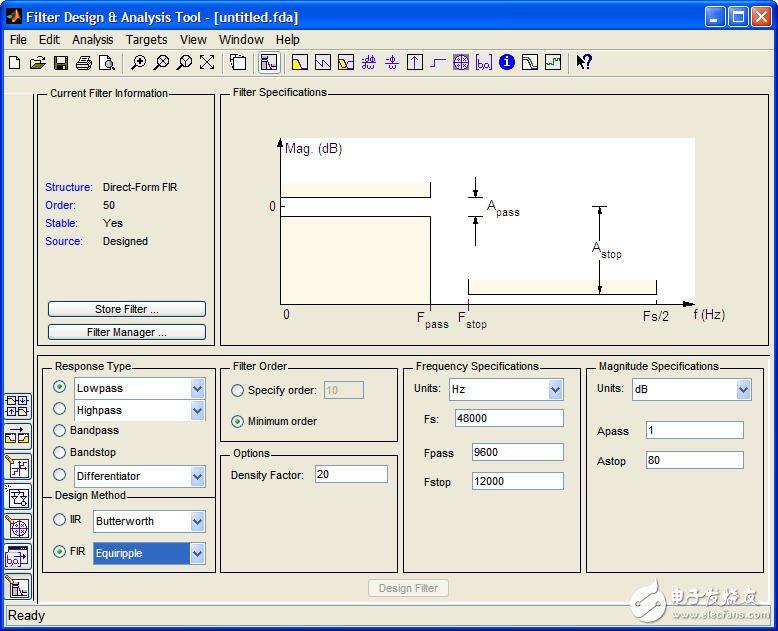
图2

滤波器的设计首先需要设置的参数：

（1） Response Type：选择FIR滤波器的类型：低通、高通、带通和带阻等。如图3所示为Lowpass中的下拉选项，在DDC/DUC模块设计中，抽取和内插需要使用Halfband Lowpass类型，而channel filter需要使用Raised-cosine类型。

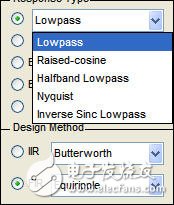
图3

（2） Design Method：FIR滤波器设计方法有多种，如图4所示，最常用的是窗函数设计法（Window）、等波纹设计法（Equiripple）和最小二乘法 （Least-Squares）等。其中窗函数设计法在学校课堂中是重点讲解的，提到FIR滤波器肯定会想到hamming、kaiser窗，但是实际应用中却很少使用，因为如果采用窗函数设计法，达到所期望的频率响应，与其它方法相比往往阶数会更多；而且窗函数设计法一般只参照通频带wp、抑制频带ws 和理想增益来设计滤波器，但是实际应用中通频带和抑制带的波纹也是需要考虑的，那在这种情况下，采用等波纹设计法就非常适用了。

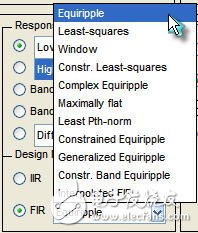
图4

（3） Filter Order：设置滤波器的阶数，这个选项直接影响滤波器的性能，阶数越高，性能越好，但是相应在FPGA实现耗用的资源需要增多。在这个设置中提供2个选项：Specify order和Minimum order，Specify order是工程师自己确定滤波器的阶数，Minimum order是让工具自动确定达到期望的频率相应所需要的最小阶数，因此具体选择哪个选项得视实际情况而定了。

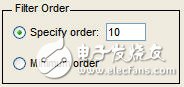
图5

（4） Frequency Specification：设置频率响应的参数，包括采样频率Fs、通带频率Fpass和阻带频率Fstop。

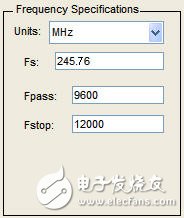
图6

参数设置完成后，FDATool就会分析并且生成滤波系数，如图7所示，可以得到滤波器的频率相应曲线，并且可以通过File-》Export导出滤波系数，如图8所示。

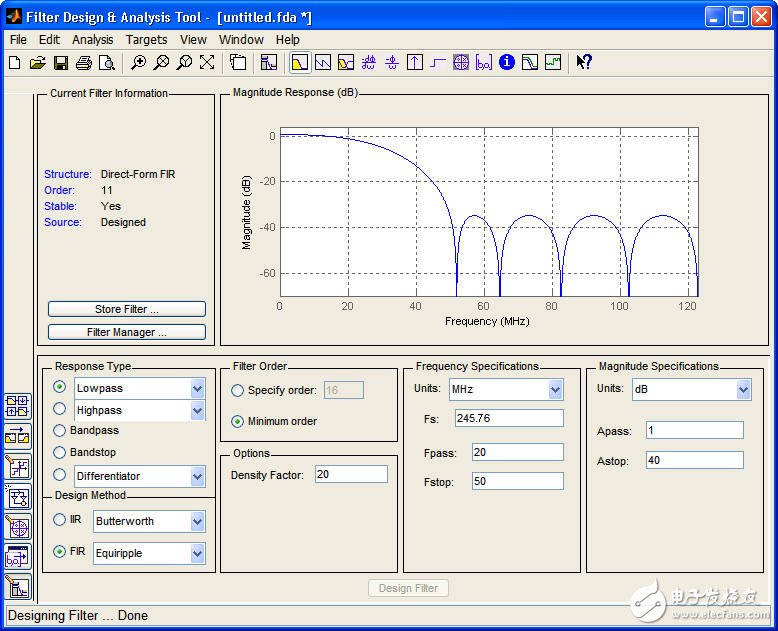
图7

图8

为了快速验证FIR滤波器的FPGA实现，使用Xilinx的System Generator工具，如图9所示为FIR滤波器的验证模型，其中通过Gateway In和Gateway out模块分隔matlab simulink模块和Xilinx FPGA模块，matlab simulink模块用于产生测试源，接收并显示滤波后波形。还有System Generator Token用于生成Xilinx FPGA模块的HDL代码。

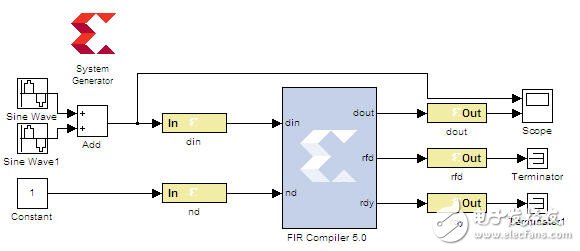
图9

其中FIR Compiler 5.0模块的参数设置如图10所示，滤波系数直接调用FDATool生成的滤波系数equ_coe，输出为全精度数据。

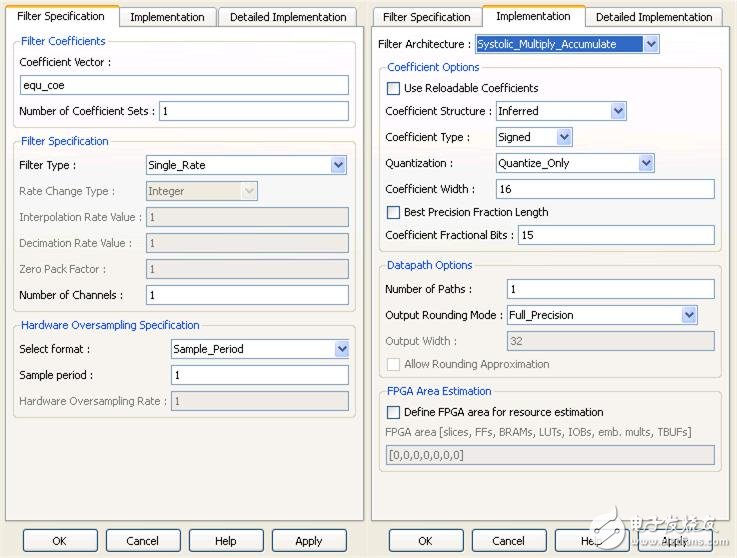
图10

得到输出结果如图11所示，上边图为输入原波形，由两个频率分量的正弦波叠加而成，频率分别为2MHz和100MHz，经过FIR滤波之后，100MHz频率分量被滤除。

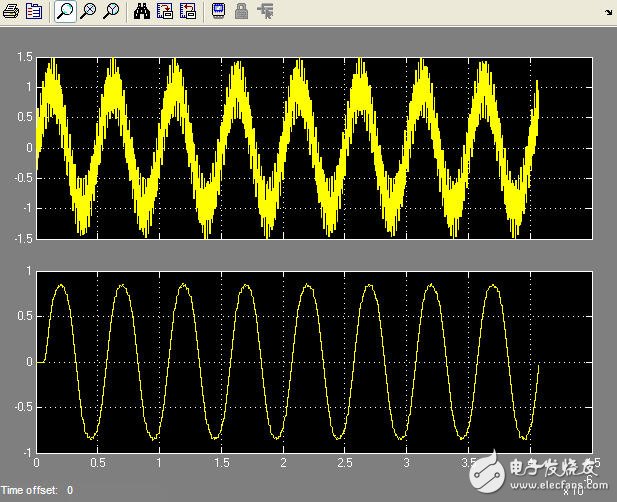
图11

FIR滤波器根据输入数据速率的不同可分为串行结构、半并行结构和全并行结构。串行结构的FIR滤波器是将并行数据串行输入，所需的DSP资源较少，但是数据吞吐率较低；而全并行结构的FIR滤波器数据是并行输入，滤波系数的个数就决定了所需DSP资源的个数，资源耗用较多，但是吞吐率可以做到很大。在大多数应用中，如无线数字中频处理，所需数据吞吐率一般都较高，因此采用的是全并行结构的FIR滤波器。

全并行FIR滤波器根据实现结构不同可分为：直接型（Transverse）、转置型（Transpose）和脉动型（Systolic），这一节主要讲解直接型FIR滤波器设计。

（一）直接型

直接型FIR滤波器在上一节中也有介绍，如图1所示，数据x（n）移入并寄存，如果有11个抽头，因此直接型FIR滤波器需要11个乘加模块。

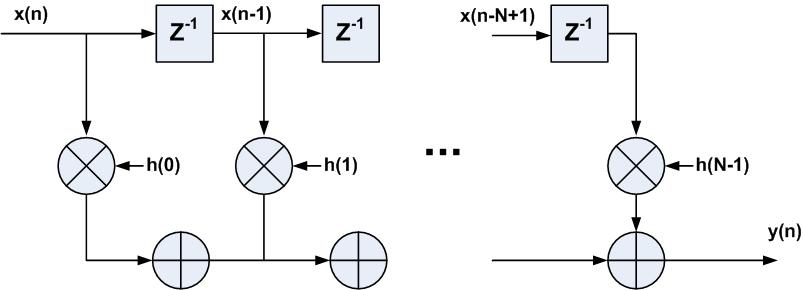
图1

FPGA实现时，直接采用上图中结构，不对中间数据寄存，则关键路径是x（n）h（0）+x（n-1）h（1）…x（n-N+1）h（N-1），以阶数10的FIR滤波器为例，如下为抽头系数：

coe_0 = -1241

coe_1 = -650

coe_2 = 1300

coe_3 = 4739

coe_4 = 8126

coe_5 = 9544

coe_6 = 8126

coe_7 = 4739

coe_8 = 1300

coe_9 = -650

coe_10 = -1241

数据输入时打了一拍，输出时打了一拍。综合后结果如下：

Number of Slice Registers： 2

Number of Slice LUTs： 19

Number of DSP48E1s： 11

关键路径中数据路径延时报告如图2所示，数据路径延时包括乘法器延时Tdspcko PCOUT AREG MULT （3.001ns）+ 10个级联加法器延时Tdspdo PCIN PCOUT（1.219），数据路径延时总共15.017ns，因此fmax最大不过66.273MHz。可以发现综合器自动将乘法器和加法器在 DSP48E1中实现。

图2

加法树实现：

直接型FIR滤波器的一般实现方法关键路径中有较多级的加法器，所有加法器延时累加后导致关键路径延时较大，对整个FIR滤波器的性能造成了很大影响。为了解决加法器延时累加的问题，可采用加法树结构，如图3所示为采用了加法数的直接型FIR滤波器结构，这种层次化的树型结构，使加法器逻辑由级联结构转化成并行结构，这样整个路径的延时减小。

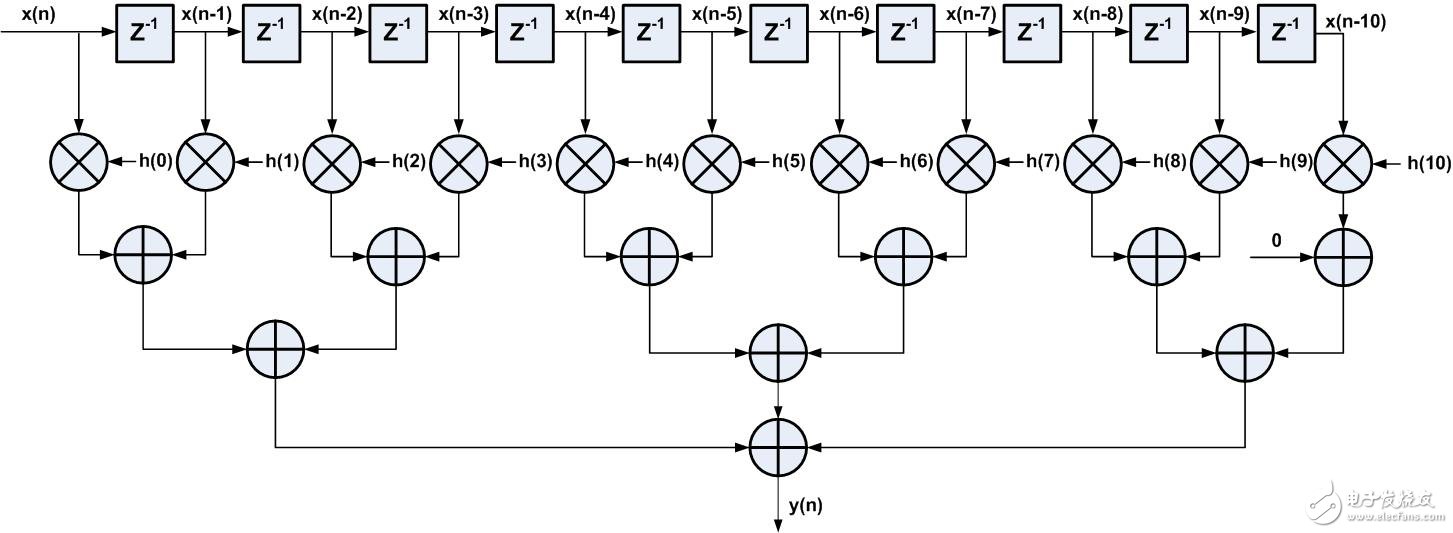
图3

流水线实现：

虽然直接型FIR滤波器采用加法树结构后优化了关键路径，但是时序还是不够理想，因为关键路径上至少有一个乘法器和一个加法器的延时，如果想竟可能的优化时序，可以分隔乘法器和加法器逻辑，中间加一级寄存器，即采用流水线实现。

那如何有效地分割逻辑呢？可以在图3中加法树结构的基础上分割，在原先的关键路径上，乘法器延时3.001ns，加法器延时1.219ns，因此可以将逻辑分割成如下**：

第1级：乘法器

第2级：2级加法器

第3级：3个数累加即2级加法器

如图4所示为流水线实现的FIR滤波器，逻辑分割后的关键路径是乘法器那一级，理论分析得到的延时只有3.001ns，如果时钟约束到250MHz可满足时序要求。

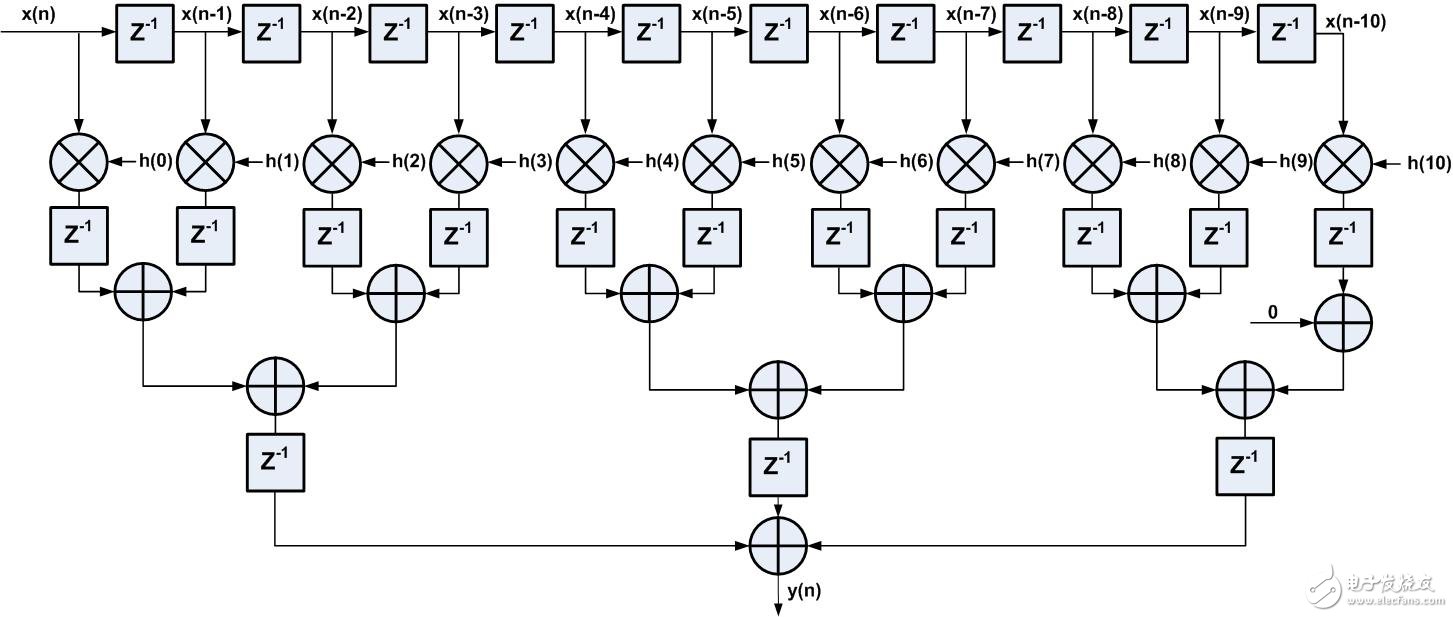
图4

实际得到综合结果如下：

Number of Slice Registers： 105

Number of Slice LUTs： 124

Number of DSP48E1s： 11

Minimum period： 3.037ns{1} （Maximum frequency： 329.272MHz）

fmax能达到329.272MHz，延时基本与预期的差不多，FIR滤波器能达到这样的性能基本能满足大多数应用了。

线性相位FIR滤波器：

FIR滤波器有一特征：线性相位，直接表现在抽头系数上，抽头系数为偶对称或者奇对称，在这节实例中，系数是偶对称的，即 h（0）=h（10），h（1）=h（9），h（2）=h（8），h（3）=h（7），h（4）=h（6），直接型FIR结构优化后如图5所示，输入数据在与系数相乘之前，因系数对称，可以先将相同系数对应的数据进行预加操作，然后再与系数相乘，如此做法的好处是是乘法器资源减少了近一半，此例中DSP资源由原先需要11个到现在只需6个。而且，在Xilinx FPGA中的DSP48E1资源专门为线性相位FIR滤波器应用提供了预加pre-adder结构，即预加和乘法都可以在1个DSP48E1中完成，这样大大缩短了数据路径的延时，有利于时序收敛。

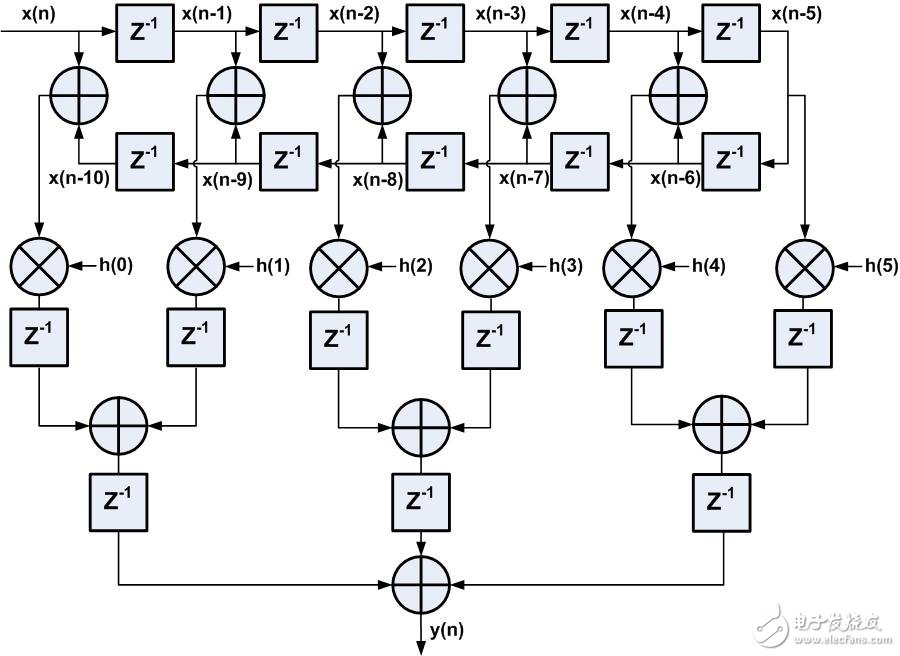
图5

实际得到综合结果如下：

Number of Slice Registers： 184

Number of Slice LUTs： 173

Number of DSP48E1s： 6

Minimum period： 2.854ns{1} （Maximum frequency： 350.385MHz）

fmax能达到350.385MHz，由于采用了加法树结构，避免了加法器级联延时，并且分了3级流水线实现。关键路径数据延时报告如图6所示，路径是从 DSP48E1输出端到dout_d，但是光从代码中看DSP48E1端到dout_d中间应该还有一级加法器的寄存，原来这个加法器采用了 DSP48E1中的累加器实现了。

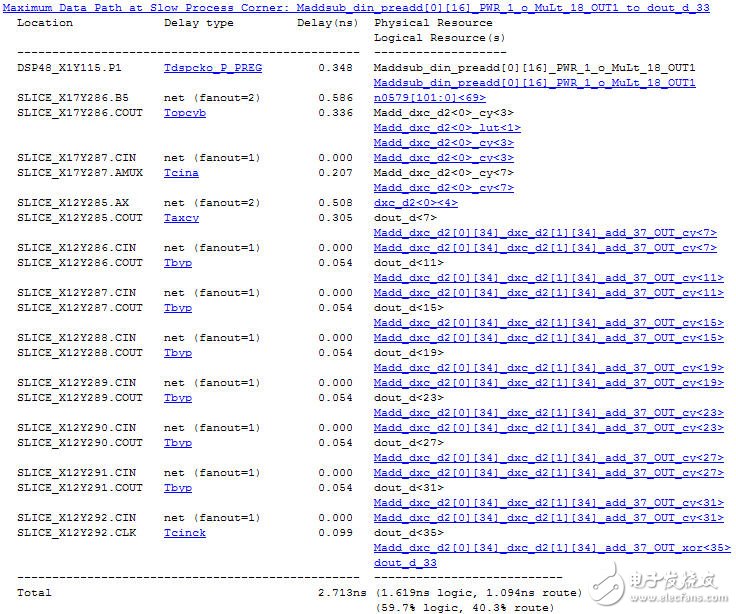
图6

FIR滤波器的单位冲激响应h（n）可以表示为如下式：

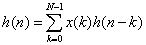
对应转置型结构的FIR滤波器，如图1所示，抽头系数与上一节中讲解直接型FIR滤波器的实例相同，滤波器阶数为10。

图1

可以发现转置型结构不对输入数据寄存，而是对乘累加后的结果寄存，这样关键路径上只有1个乘法和1个加法操作，相比于直接型结构，延时缩短了不少。

综合得到结果如下：

Number of Slice Registers： 1

Number of Slice LUTs： 18

Number of DSP48E1s： 11

Minimum period： 4.854ns{1} （Maximum frequency： 206.016MHz）

关键路径延时报告如图2所示，其中乘累加操作延时Tdspdck_A_PREG_MULT 2.655ns；另外还有一项net delay居然有1.231ns，如此大是因为fanout=11，仔细研究可以发现在h（n）表达式中x（n）与所有11个抽头系数进行了乘法操作，因此fanout达到了11，这也是转置型FIR滤波器的缺点：输入数据的fanout过大。

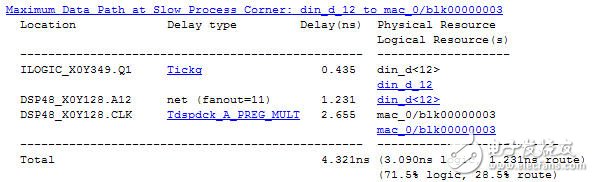
图2

线性相位：

与直接型结构相同，由FIR滤波器的线性相位特征，转置型结构的FIR滤波器也可优化，如图3所示为线性相位FIR滤波器转置型结构，总共11个抽头系数，其中5对系数两两相同，因此可以省去5个乘法器，采用6个DSP资源实现转置型FIR滤波器。

图3

流水线实现：

为了进一步缩短关键路径的延时，将乘法器和加法器逻辑分割开，中间加入流水线级，结果如图4所示，在线性相位结构的基础上，加入一级寄存器，这样最大限度上优化时序。

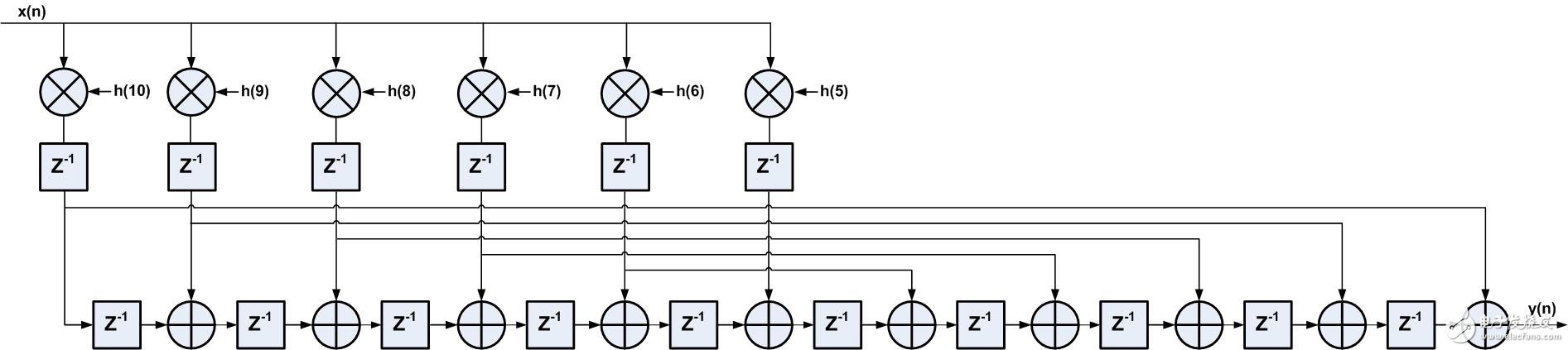
图4

综合得到结果如下：

Number of Slice Registers： 355

Number of Slice LUTs： 340

Number of DSP48E1s： 6

Minimum period： 3.861ns{1} （Maximum frequency： 259.000MHz）

如图5所示为与图2中相对应路径的延时报告（图2由ISE的Timing Analysis工具产生，图5是由PlanAhead的Timing Analysis工具产生），其中由于采用线性相位结构，输入信号的fanout只有6，延时从原先的1.231ns减小到1.01ns；并且分隔乘法器和加法器逻辑之后，关键路径上只有乘法器的延时：1.42ns。

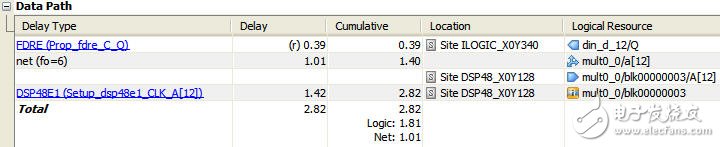
图5

脉动型(Systolic)FIR滤波器设计#e#

脉动型FIR滤波器是对直接型的升级，在每个操作后都加入流水线级，每个动作都打一拍，就跟心脏跳动一样，因此称为脉动型，这种结构非常适用于高速数据流的处理。如图1所示为脉动型FIR滤波器结构。

图1

与直接型结构不同的是，输入数据到下一个处理单元都需要打2拍，这是为了使乘法后的累加数据同步，下面推导验证：

x（n）为输入数据，yt（n）为直接型结构的输出

yt（n）=x（n）h（0）+x（n-1）h（1）+x（n-2）h（2）…x（n-10）h（10）

ys（n）为脉动型结构的输出，如图1中有P1、P2…P10共10个节点

P1=x（n-4）h（0）

P2=（P1 + x（n-5）h（1））*Z-1=x（n-5）h（0） + x（n-6）h（1）

…

P10=（P9 + x（n-23）h（10））*Z-1

ys（n）=x（n-14）h（0） + x（n-15）h（1） + … + x（n-23）h（9）+ x（n-24）h（10）

由ys（n）和yt（n）的表达式，可以推导出ys（n）=yt（n-14）

因此脉动型FIR滤波器的延迟较大

如图2所示为11抽头系数脉动型FIR滤波器FPGA实现结构（实例与前几节相同），穿了一层“衣服”，采用Xilinx FPGA中的DSP48E1 实现，基本处理单元中的操作都可在一个DSP48E1中完成，输入数据经过DSP48E1中寄存2拍后通过ACOUT输出，直接连接到下一个 DSP48E1中的ACIN端口，累加输出PCOUT直接连接到下一个DSP48E1中的PCIN端口，这些连接都没有经过FPGA的Fabric连线逻辑，而是通过DSP Block的内部走线连接，这样实现能够缩短路径的延时。

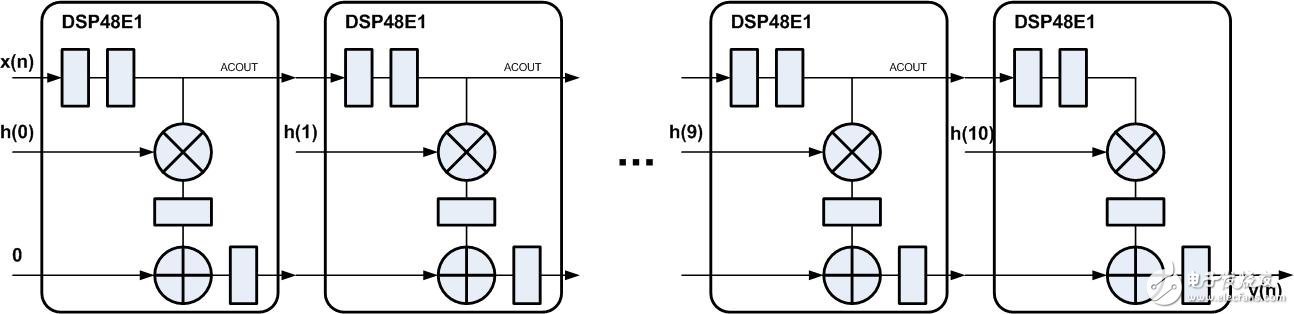
图2

编写了相关代码，综合结果如下：

Number of Slice Registers： 4

Number of Slice LUTs： 19

Number of DSP48E1s： 11

Minimum period： 3.006ns{1} （Maximum frequency： 332.668MHz）

线性相位实现：

与前几节相同，由于FIR滤波器的线性相位特性，相对应有线性相位的实现结构，如图3所示，利用DSP48E1中预加器实现乘法前的加法操作。对于脉动型 FIR滤波器的线性相位结构有很多注意点，其中预加器数据的配对，常规情况下，此例中应是x（n）和x（n-10）、x（n-1）和x（n-9）、 x（n-2）和x（n-8）、x（n-3）和x（n-7）、x（n-4）和x（n-6），而图3中结构，加入了延时11的移位寄存器，预加器配对的数据为 x（n-2）和n（n-12）、x（n-4）和x（n-12）、x（n-6）和x（n-12）、x（n-8）和x（n-12）、x（n-10）和x（n- 12），可以发现预加器配对数据中有一个数据始终是x（n-12），但是每一个配对数据的相对延时与常规情况下相同：10、8、6、4和2。

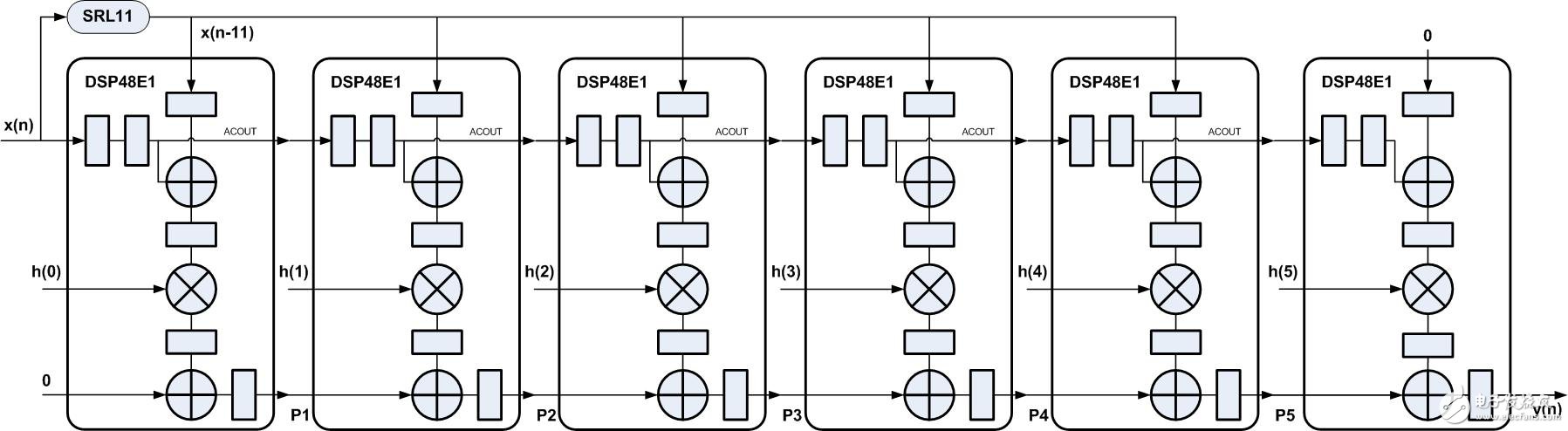
图3

而各节点P1、P2、P3、P4、P5和y（n）的表达式如下

P1=x（n-5）h（0） + x（n-15）h（0）

P2=（ P1 + （x（n-6）h（1） + x（n-14）h（1）） ）Z-1=x（n-6）h（0） + x（n-16）h（0） + x（n-7）h（1） + x（n-15）h（1）

P3=（ P2 + （x（n-8）h（2） + x（n-14）h（2）） ）Z-1=x（n-7）h（0） + x（n-17）h（0） + x（n-8）h（1） + x（n-16）h（1） + x（n-9）h（2） + x（n-15）h（2）

P4=（ P3 + （x（n-10）h（3） + x（n-14）h（3）） ）Z-1=x（n-8）h（0） + x（n-18）h（0） + x（n-9）h（1） + x（n-17）h（1） + x（n-10）h（2） + x（n-16）h（2） + x（n-11）h（3） + x（n-15）h（3）

P5=（ P4 + （x（n-12）h（4） + x（n-14）h（4）） ）Z-1=x（n-9）h（0） + x（n-19）h（0） + x（n-10）h（1） + x（n-18）h（1） + x（n-11）h（2） + x（n-17）h（2） + x（n-12）h（3） + x（n-16）h（3） + x（n-13）h（4） + x（n-15）h（4）

y（n）=（P5 + x（n-14）h（5））Z-1= x（n-10）h（0） + x（n-20）h（0） + x（n-11）h（1） + x（n-19）h（1） + x（n-12）h（2） + x（n-18）h（2） + x（n-13）h（3） + x（n-17）h（3） + x（n-14）h（4） + x（n-16）h（4） + x（n-15）h（5）

因抽头系数对称，由h（0）=h（10），h（1）=h（9），h（2）=h（8），h（3）=h（7），h（4）=h（6）可得

y（n）= x（n-10）h（0） + x（n-11）h（1） + x（n-12）h（2） + x（n-13）h（3） + x（n-14）h（4） + x（n-15）h（5） + x（n-16）h（6） + x（n-17）h（7） + x（n-18）h（8） + x（n-19）h（9） + x（n-20）h（10）

验证得到y（n）=yt（n-10），比普通脉动结构延时小，但是相比于其他结构的FIR滤波器延时还是较大的。

编写了相关代码，综合结果如下：

Number of Slice Registers： 84

Number of Slice LUTs： 99

Number of DSP48E1s： 6

Minimum period： 3.256ns{1} （Maximum frequency： 307.125MHz）

在DSP in FPGA： FIR滤波器设计（一）、（二）中分别讲解了直接型、转置型和脉动型结构FIR滤波器的实现方法，这三种结构是FPGA实现中比较常用的方法，以下对这三种结构做一个比较：

（1） 直接型：方法简单易实现，但是使用加法树优化后增加了功耗

（2） 转置型：关键路径延时较小，时序易满足，但是输入数据扇出较大，不适用于阶数较高的滤波器实现

（3） 脉动型：适用于高速数据处理，但是延时相比于其它结构较大