1、前言

分频器是FPGA设计中使用频率非常高的基本单元之一。尽管目前在大部分设计中还广泛使用集成锁相环(如Altera的PLL，Xilinx的DLL)来进行时钟的分频、倍频以及相移设计，但是，对于时钟要求不太严格的设计，通过自主设计进行时钟分频的实现方法仍然非常流行。首先这种方法可以节省锁相环资源，再者这种方式只消耗不多的逻辑单元就可以达到对时钟的操作目的。

2、整数倍分频器的设计

2.1 偶数倍分频

偶数倍分频器的实现非常简单，只需要一个计数器进行计数就能实现。如需要N分频器(N为偶数)，就可以由待分频的时钟触发计数器进行计数，当计数器从0计数到N/2-1时，将输出时钟进行翻转，并给计数器一个复位信号，以使下一个时钟开始从零计数。以此循环，就可以实现偶数倍分频。以10分频为例，相应的verilog代码如下：

regclk_div10;

reg [2:0]cnt;

always@(posedge clk or posedge rst) begin

if(rst)begin //复位

cnt<=0;

clk_div10<=0;

end

elseif(cnt==4) begin

cnt<=0; //清零

clk_div10<=~clk_div10; //时钟翻转

end

else

cnt<=cnt+1;

end

2.2 奇数倍分频

奇数倍分频因占空比不同，主要有以下两种方法。对于非50%占空比的分频，与偶数倍分频类似，只需要一个计数器就能实现特定占空比的时钟分频。如需要1/11占空比的十一分频时钟，可以在计数值为9和10时均进行时钟翻转，该方法也是产生抽样脉冲的有效方法。相应的verilog代码如下：

always @(posedge clk or posedge rst) begin

if(rst)begin //复位

cnt<=0;

clk_div11<=0;

end

elseif(cnt==9) begin

clk_div11<=~clk_div11; //时钟翻转

cnt<=cnt+1; //继续计数

end

elseif(cnt==10) begin

clk_div11<=~clk_div11; //时钟翻转

cnt<=0; //计数清零

end

else

cnt<=cnt+1;

end

对于50%奇数分频器的设计，用到的思维是错位半个时钟并相或运算。具体实现步骤如下：分别利用待分频时钟的上升沿与下降沿进行((N-1)/2)/N分频，最后将这两个时钟进行或运算即可。以三分频为例，相应的电路原理图和时序仿真图如图1和图2所示，相应代码如下：

reg clk1;

reg[1:0]cnt1;

always@(posedge clk or posedge rst) begin

if(rst)begin //复位

cnt1<=0;

clk1<=0;

end

elseif(cnt1==1) begin

clk1<=~clk1; //时钟翻转

cnt1<=cnt1+1; //继续计数

end

elseif(cnt1==2) begin

clk1<=~clk1; //时钟翻转

cnt1<=0; //计数清零

end

else

cnt1<=cnt1+1;

end

reg clk2;

reg[1:0]cnt2;

always@(negedge clk or posedge rst) begin

if(rst)begin //复位

cnt2<=0;

clk2<=0;

end

elseif(cnt2==1) begin

clk2<=~clk2; //时钟翻转

cnt2<=cnt2+1; //继续计数

end

elseif(cnt2==2) begin

clk2<=~clk2; //时钟翻转

cnt2<=0; //计数清零

end

else

cnt2<=cnt2+1;

end

assignclk_div3=clk1 | clk2; //或运算

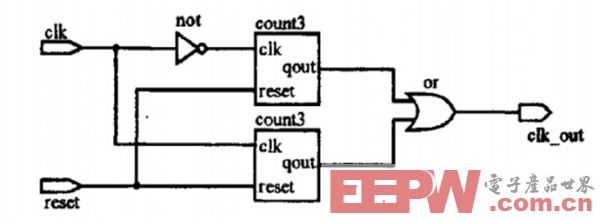
图1 50%占空比的三分频电路原理图

图2 50%占空比的三分频时序仿真图

3、小数倍分频器的设计

3.1 半整数分频器

半整数N+0.5分频器设计思路：首先进行模N+1的计数，在计数到N时，将输出时钟赋值为1，而当回到计数0时，又赋值为0，这样，当计数值为N时，输出时钟才为1。因此，只要保持计数值N为半个时钟周期即是该设计的关键。从中可以发现。因为计数器是通过时钟上升沿计数，故可在计数为N时对计数触发时钟进行翻转，那么，时钟的下降沿就变成了上升沿。即在计数值为N期间的时钟下降沿变成了上升沿。也就是说，计数值N只保持了半个时钟周期。由于时钟翻转下降沿变成上升沿，因此，计数值变为0。所以，每产生一个N+0.5分频时钟的周期，触发时钟都要翻转一次。图3给出了通用半整数分频器的电路原理图。以2.5倍分频为例，相应的电路verilog代码如下，时序仿真图如图4所示。

//异或运算

assignclk_in=clk^clk_div2;

//模3计数器

reg clk_out;

reg [1:0]cnt;

always@(posedge clk_in or posedge rst) begin

if(rst)begin //复位

cnt<=0;

clk_out<=0;

end

elseif(cnt==1) begin

clk_out<=~clk_out; //时钟翻转

cnt<=cnt+1; //继续计数

end

elseif(cnt==2) begin

clk_out<=~clk_out; //时钟翻转

cnt<=0; //计数清零

end

else

cnt<=cnt+1;

end

//2分频

reg clk_div2;

always@(posedge clk_out or posedge rst) begin

if(rst) clk_div2<=0; //复位

else clk_div2=~clk_div2;

end

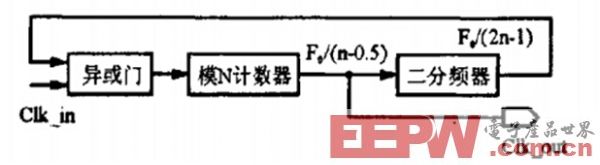
图3 通用半整数分频器的电路原理图

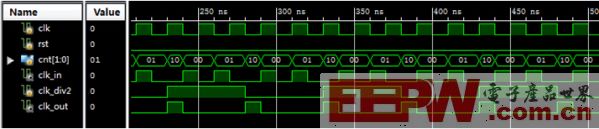
图4 2.5倍分频器时序仿真图

3.2 任意小数分频器

小数分频器的实现方法有很多中，但其基本原理都一样的，即在若干个分频周期中采取某种方法使某几个周期多计或少计一个数，从而在整个计数周期的总体平均意义上获得一个小数分频比。一般而言，这种分频由于分频输出的时钟脉冲抖动很大，故在设计中的使用已经非常少。但是，这也是可以实现的。以8.7倍分频为例，本文仅仅给出双模前置小数分频原理的verilog代码及其仿真图(如图6)，具体原理可以参考刘亚海的《基于FPGA的小数分频器的实现》以及毛为勇的《基于FPGA的任意小数分频器的设计》。

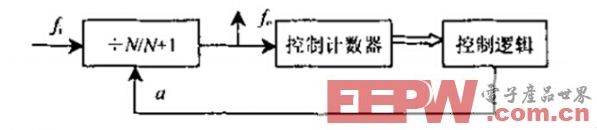
图5 小数分频器的电路原理图

//8分频

reg clk_div8;

reg[2:0]cnt_div8;

always@(posedge clk or posedge rst) begin

if(rst)begin //复位

clk_div8<=0;

cnt_div8<=0;

end

elseif(cnt_div8==3'd7) begin

clk_div8<=1; //置1

cnt_div8<=0;

end

elseif(cnt_div8==3'd0) begin

clk_div8<=0; //置0

cnt_div8<=cnt_div8+1;

end

else

cnt_div8<=cnt_div8+1;

end

//9分频

reg clk_div9;

reg[3:0]cnt_div9;

always@(posedge clk or posedge rst) begin

if(rst)begin //复位

clk_div9<=0;

cnt_div9<=0;

end

elseif(cnt_div9==3'd8) begin

clk_div9<=1; //置1

cnt_div9<=0;

end

elseif(cnt_div9==3'd0) begin

clk_div9<=0; //置0

cnt_div9<=cnt_div9+1;

end

else

cnt_div9<=cnt_div9+1;

end

//控制信号

parameterDiv8Num=3;

reg ctrl;

reg[3:0]AddValue;

always@(posedge clk or posedge rst) begin

if(rst)begin //复位

ctrl<=0;

AddValue<=10-7;

end

elseif(AddValue<10) begin

ctrl<=0;

AddValue<=AddValue+Div8Num;

end

else begin

ctrl<=1;

AddValue<=AddValue-10;

end

end

//选择输出

reg clk_out;

always @(ctrlor posedge clk or posedge rst) begin

if(rst) clk_out<=0; //复位

elseif(ctrl) clk_out<=clk_div8;

elseclk_out<=clk_div9;

end

图6 8.7分频器的时序仿真图

4、总结分频器是FPGA的基础，而且在FPGA逻辑电路设计的时候是经常使用的，希望大家对以上的整数倍分频和半整数倍分频能熟练掌握