0 引言

在超声流量检测过程中，由于环境噪声使得流量检测的精度收到了严重的影响。目前多采用软件滤波的方法，对采集回来的声波信号进行数字处理，以提高检测的精度。此类方法对硬件处理器的运算能力要求较高，而且会影响检测的实时性。随着微电子技术的不断进步，FPGA的容量和处理速度已有了飞跃性的提高。特别是在数字信号处理方面，其性能已经超过了某些专用的信号处理芯片。本文在的超声波流量检测信号采样处理电路中，采用FPGA实现了声波信号的高速缓存和FIR滤波器，不仅达到了预期的消噪效果，而且提高了系统运行速度和集成度。下面将介绍FIR滤波器的具体实现过程。

1 数字滤波原理与设计

FIR数字滤波器的特性可以用它的系统转移函数或差分方程来描述。一般地，线性是不变离散系统的差分方程，可表示为：

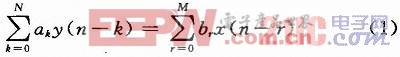
式中：zr，pk分别为H(z)的M个零点和N个极点，它们由系统的形式和各系统参数ak，br所决定。FIR滤波器都是非递归形式的滤波器。

此系统的输出只与输入x(n)，x(n-1)，…有关，而与系统过去的输出y(n-1)，y(n-2)，…无关，此即非递归滤波器。

滤波器设计采用Matlab中的FDA Tool计算带通滤波器系数。滤波器采用Kaiser窗函数设计，采样频率为40 MHz，窗上下截止频率分别为3 MHz和7 MHz。由此得到的滤波器系数为：

2 FIR滤波器的FPGA实现

由式(4)可知，FIR滤波器的数学表达式就是卷积运算，也就是做乘加运算。例如，一个M阶的FIR滤波器的输出是输入样本的M个依次值的加权和，加权系数就是此滤波器的单位冲激响应值。对于上节设计的10阶线性FIR滤波器，可以得到：

这样，10阶FIR滤波器的结构可以描述为：输入样本x(n)经过10阶移位寄存器延迟后得到10个具有不同延迟的抽头，将对称的抽头值相加后再与相应的权系数相乘，5个乘积相加就得到滤波器的输出值。滤波器结构如图1所示。

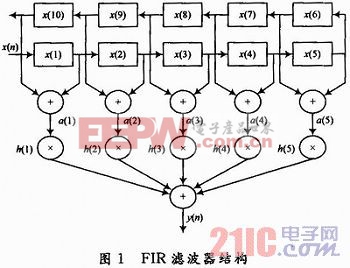
滤波器抽头与权系数之间存在着乘法运算，在硬件实现中乘法运算是相当复杂的运算，不仅占用大量硬件资源，而且运算速度较慢。为了提高运算速度，在此利用FPGA逻辑单元(LE)中的查找表实现替代乘法运算的查表运算。为了说明方便，在此以4阶滤波器为例，数据为2位的二进制整形。设a(1)=01，a(2)=11，h(1)=10，h(2)=01，权系数与抽头之间的乘加运算如图2所示。

图2中，P1(n)为抽头低位与权系数的乘积结果，P2(n)为抽头高位与权系数的乘积结果，在此称之为单位积。常规的计算顺序是先将P1(n)和P2(n)的对应项在垂直方向上移位相加，所得结果再进行水平方向上相加。但是从图中可以看出，先将P1(n)和P2(n)在水平方向上相加，然后再进行垂直方向上移位相加，所得的结果是一样的。第二种顺序中，P1(n)和P2(n)是h(n)和a(n)的某个比特位的乘积，而对于设计好的FIR滤波器h(n)是固定的，这样就可以通过a(n)某比特位的组合来查表求出P1(n)或P2(n)，并在水平方向上实现求和。如表1所示，a1(n)表示a(n)的低位组合，单位积P1表示相应的权系数和。

对于a(n)的高位组合，单位积P2可以建立同样的组合表。将P1和P2移位相加，即可得到滤波器的输出结果。在此例中采用的是2位二进制的权系数和输入样本，对于高精度的权系数和输入样本，只不过是增加更多的单位积P3，P4，…等等。

实际操作过程中，基于FPGA的FIR滤波器通过三步完成，第一步将输入信号x(n)进行移位延迟，形成n阶抽头，再将相互对称的抽头相加得到滤波器抽头；第二步在FPGA中构造ROM，按前一步产生的滤波器抽头进行查表运算；最后将所有位的查表运算结果移位相加得到滤波器输出y(n)。

3 试验结果分析

采用Altera公司的FPGA器件EPF10K30实现10阶的带通FIR滤波器进行试验。A／D采样频率为40 MHz，精度为12位，声波中心频率为5M-Hz。A／D采样得到的原始声波信号如图3所示。经过FIR滤波器处理后的声波信号如图4所示。

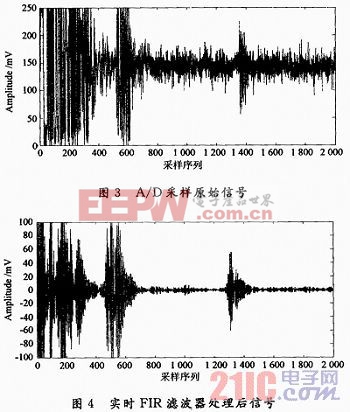
试验结果表明，采用FPGA实现的FIR滤波器有效地消弱了噪声干扰，在保证实时性的基础上，为后期处理提供了可靠的数据。

4 结论

针对超声波信号中的噪声采用基于FPGA的FIR滤波，提高了硬件电路的集成度，并取得了良好的消噪效果。在硬件实现过程中采用查表方法替代滤波过程中的乘法运算，节省了占用的片内资源，提高了处理速度。同时由于采用了并行硬件算法，其处理速度远高于CPU或DSP上的程序处理速度。