巧找线性系统稳定性的“七寸”
时间:09-29 13:08 阅读:3189次
*温馨提示:点击图片可以放大观看高清大图
简介:在电子电路设计过程中,负反馈的引入让系统变的更加“听话”,然而,在使用负反馈的过程中,也有潜在的不稳定性:当设计的系统满足一定条件时,设计的系统就会变得不那么“听话”,甚至变得振荡起来。为了找到负反馈线性系统的稳定性,本文对关键点进行剖析。
为分析系统的稳定性,首先需要知道两个概念:增益交点和相位交点。所谓增益交点,顾名思义,就是使环路增益为1的频率点;相位交点是使环路增益的相位为-180°的频率点。这两个频率点在保持系统的稳定性中,起到重要的作用。在稳定的系统中,增益交点通要比相位交点靠前:

在图1中,增益交点在相位交点之前,满足系统稳定的条件,这样的系统变得稳定,而图2中增益交点在相位交点之后,则系统就变得不稳定。
为什么这么说呢?因为这就是非常著名的“巴克豪森判据”(Barkhausen’s Criteria)。因此,负反馈的引入就是为了克服这样两个因素。
由此可以看出,一个系统的波特图对判断一个系统的稳定与否有着重要的作用。如果设计出了如图2的系统,显然不稳定,但是可以通过对系统的反馈回路调整和补偿,将系统的增益交点出现在相位交点之前,那么,系统就会变得稳定了。
写到这里,相信不少电子工程师对波特图的使用有了更深刻的认识,有兴趣的朋友参考下我之前写的文章欣赏波特图的魅力,在这里我要强调一点,在画波特图的相位图时,需要找好三个关键点:
①对于零点频率ω,在0.1ω处,相位图开始下降;
②在ω处,相位图的经过了大约+45°的相移;
③在10ω处,相位图经过了大约90°的相移;
为说明这点,现以一RC低通滤波器为例说明:
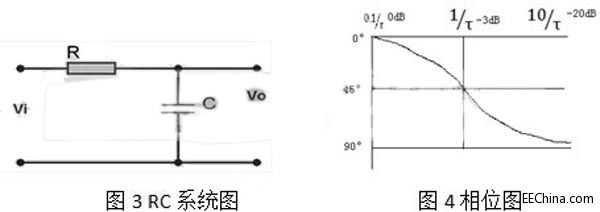
其传递函数为
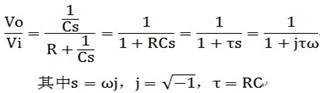
其相位图如图4 所示。
波特图能够大概分析系统稳定性,在设计过程中,如果系统不复杂,能够以表达式的形式表达出极点,那么,也可以在复平面中查看系统的稳定性。(由于传递函数长用拉普拉斯变换,引入拉普拉斯算子s,这让我深深明白大学学习复变函数的重要性)。
对于复平面,图5,
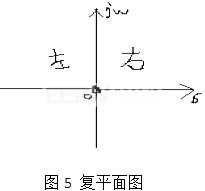
若极点落在右半平面,则系统是不稳定的,若在原点处,系统也有可能出在振荡状态。也就是说,只有所有的极点都落在左平面内,系统才能变得稳定。(这时,你能想起来大学老师教你的复变函数的一个应用了吧)。
例如若一极点的位置为1+J3,则系统不稳定,若极点位置在-1+j3,那么就是稳定的。所以,在设计系统时,要将所有的极点都落在复平面的右半平面。