关键词:LMS自适应滤波算法;变步长;系统识别;滤波性能

中图分类号:TN911.7 文件标识码:A 文章编号:1003-7241(2013)06-0032-05

1 引言

自适应滤波是研究结构和参数可以改变或调整的系统,利用前一时刻获得的结果,自动的调节现时刻的参数以获得最佳滤波参数,以适应信号或噪声未知或统计特性随时间变化的情况,从而实现最优滤波。我们无须知道信号的结构和先验知识,也无须精确设计信号处理系统的结构和参数。自适应过程是一个不断逼近目标的过程。其中最小均方误差算法(即LMS算法)尤为常用。1960年Widrow和Hoff提出最小均方误差(LMS)算法,由于其具有的简单性、鲁棒性和易于实现的性能,因此在很多领域得到了广泛的应用。

基于最陡下降法的最小均方误差算法(LMS)的迭代公式如下:

其中,W(n)为自适应滤波器在n时刻的权矢量,X(n)为n时刻的输入信号矢量,d(n)为期望信号输出值,e(n)为期望值与滤波器输出值的误差值。μ为步长因子。该算法收敛的条件是:

收敛速度、时变系统跟踪能力和稳态失调误差是衡量自适应滤波算法性能优劣的三个主要指标。传统LMS算法的固定步长μ在满足收敛速度、时变系统跟踪能力和稳态失调误差之间的要求存在很大矛盾。的步长μ确保稳态时具有小的失调,但是算法的收敛速度慢,并且对非稳态系统的跟踪能力差。另一方面,大的步长μ使算法具有更快的收敛速度和好的跟踪能力,但这是以大的失调为代价的。为了克服这一矛盾,人们提出了变步长自适应滤波算法,所谓变步长就是在初始收敛阶段或未知系统参数发生变化时,步长自适应增大,以便有较快的收敛速度和对系统的跟踪速度;在算法收敛之后不管扰动有多大,应保持较小的步长以达到较小的稳态失调误差。

R.D.Gitlin[1]曾提出了一种变步长自适应滤波算法,其步长因子μ(n)随迭代次数的增加而逐渐减小;Yasukawa[2]等提出了使步长因子μ(n)正比于误差信号的大小,但这两种改进算法对主输入端的干扰信号非常敏感,干扰信号越大,误差越大,步长也就越大导致不易收敛。文献[3]提出了使步长因子μ(n)正比于误差信号e(n)与输入信号X(n)的互相关函数,然而计算复杂量大大增加了。文献[4]提出了基于Sigmoid函数变步长LMS算法,但在e(n)趋近于0处变化太大,不具有缓慢变化的特征。在此基础上文献[5]进行了改进,克服了sigmoid函数的缺点,但该算法受噪声影响较大,在稳态阶段,失调误差仍很大。Kwong[6]等提出的VSSLMS算法使步长因子μ(n)与均方瞬时误差建立函数关系,但是受观测噪声的影响大。文献[7]提出了利用当前误差和上一次误差的自相关函数来控制步长的变化,消除了不相关噪声的干扰。

本文在对文献[6]、文献[7]和文献[8]分析的基础上提出了一种改进算法,并应用在系统辨识中。针对系统辨识的输入信号具有强相关性时,利用了解相关。

2 VSSLMS算法

在VSSLMS算法中,步长迭代表达式如下:

α为步长的遗忘因子,其取值不能超过1,否则算法不收敛,如果取值太小,当算法收敛时,步长变化太快,造成稳态误差较大,所以α的取值是小于1而接近1;β决定步长因子受误差的影响程度,当算法收敛后,误差较小,为了得到较小的μ值,所以β的取值一般很小。

如上所说,步长因子μ(n)与均方瞬时误差建立函数关系,受噪声影响的,导致在算法收敛后的稳态失调误差仍然很大。

3 改进变步长LMS算法

在对文献[6]、文献[7]和文献[8]分析的基础上,提出了一种改进的变步长因子调节方式,本文的自适应滤波算法表示如下:

步骤一如式(1);

变步长表达式为:

其中,λ是遗忘因子,其取值小于1接近1;p(n)是误差遗忘量累加的均值,α、β同VSSLMS算法。

M为一正实数,为了减少计算量,一般可以取2或3。

步长因子也就随着增大,所以新算法对时变系统的跟踪能力强。

4 解相关

前面分析的具有较好的滤波效果是建立在输入信号x(n)与x(n-1)不相关或相关性弱的基础上,如果它们之间有较强的相关性就要进行解相关。

可以把看成是与的相关部分,这个运算过程相当于解相关运算,不仅降低了强相关输入信号的相关性,而且还可以加快收敛速度。

根据文献[9]的解相关过程,本文在解相关下的自适应滤波算法过程如下:

步骤1如式(1);

5 仿真实验

本文通过其在系统辨识中的应用,来检验改进的LMS算法的性能,用matlab进行仿真实验,实验仿真模型如图2所示。

(4) 输入信号分别为不相关信号和强相关信号,在不同信噪比环境下的实验结果。

分别作100次独立实验,采样点数为1000点,然后求其统计平均,得出学习曲线后进行平滑处理。

实验1:参考输入信号X(n)为零均值,方差为1的高斯白噪声,V(n)为与X(n)不相关的高斯白噪声,其均值为零,方差为0.04。仿真结果如图3所示,[1]是传统LMS算法,μ=0.01;[2]是VSSLMS算法,α=0.99,β=4.8*1e-3;[3]是改进的LMS算法,α=0.98,β=4.8*1e-2,λ=0.99。从图中可以看出,在高信噪比环境中,三种算法在相同稳态失调误差的条件下,改进算法有更快的收敛速度。

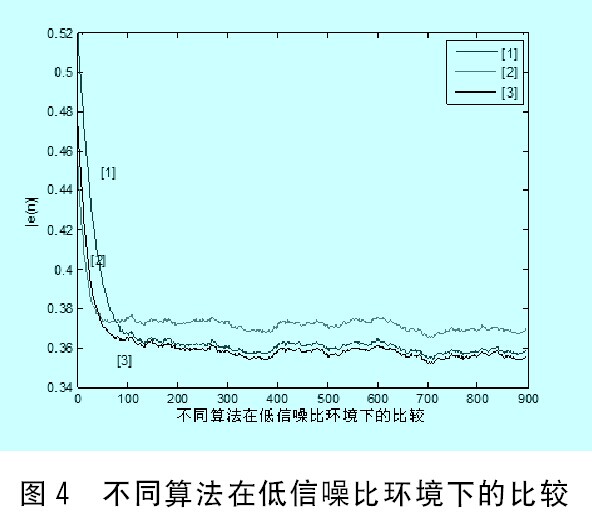
实验2:参考输入信号X(n)为零均值,方差为1的高斯白噪声,V(n)为与X(n)不相关的高斯白噪声,其均值为零,方差为0.4。VSSLMS算法中的α=0.98,改进算法中的β=4.8*1e-3,其余参数设置如实验1。仿真结果如图4所示,从图中可以看出,在低信噪比环境中,改进算法有更快的收敛速度和更小的稳态失调误差。

实验3:参考输入信号X(n)为零均值,方差为1的高斯白噪声,V(n)为与X(n)不相关的高斯白噪声,其均值为零,方差为0.04。未知系统在第500点的时候发生突变。参数设置如实验1。仿真结果如图5所示,从图中可以看出,改进算法有较好的跟踪能力和更小的稳态失调误差。

实验4:输入信号是均值为0方差为1的高斯白噪声通过一个AR模型所得为,a(n)是均值为0方差为1的高斯白噪声,V(n)为0方差为0.04的高斯白噪声。 [1]是未经过解相关的改进算法中,α=0.997,β=4.8*1e-6,λ=0.99;[2]经过解相关的改进算法中,α=0.98,β=4.8*1e-3,λ=0.99。仿真结果如图6所示,从图中可以看出,在输入信号具有强相关性时,经过解相关的改进算法在稳态失调误差一致的条件下,有更快的收敛速度。

6 结束语

本文提出的改进的变步长算法,通过在系统辨识及发生突变情况下的仿真实验下表明,具有更快的收敛速度、更小的稳态失调误差和较好的跟踪能力。对于强相关输入信号经过解相关后,也具有更快的收敛速度。

参考文献:

[1] Gitlin R D,Weinstein S D.On the design of gradient algorithms for digitally implemented adaptive filters [J].IEEE Trans on CT.1973,(2):125-136.

[2] Yasukawa H,Shimada S,Furukrawa I,et al.Acou-stic Echo Canceller with High Spee-ch Quality [C].CASSP,87:2125-2128.

[3] Shan T J,Kailaith T.Adaptive algorithm with an automatic gain control feature [J].IEEE Trans on Acoust,speech,and signal processing (S0096-3518),1991,35(1):122-127.

[4] 罩景繁,欧阳景正.一种改进的变步长自适应滤波算法[J].数据采集与处理,1997,12(3):171-194.

[5] 高鹰,谢胜利.一种变步长LMS自适应滤波算法及分析[J].电子学报,2001,29(7):1094-1097.

[6] Kwong R H,Johnston E W.A variable step size LMS algorithm [J].IEEE Trans. on Signal process-ing (S1053-587X),1992,40(7):1663-1664.

[7] Tyseer Aboulnasr,Member,IEEE,and K.[7] Tyseer Aboulnasr,Member,IEEE,and K.Mayyas.A Robust Variable Step-Size LMS Type Algorithm:Analysis and Simulations [J].IEEE transactions on circuits an-d systems-II analog and digital signal processing,1997,45(3):631-639.

[8] 李竹,杨培林,行小帅.一种改进变步长LMS算法及其在系统辨识中的应用[J].仪器仪表学报,2007,28(7):1340-1344.

[9] John F.oherty,Senior Member,IEEE,and Rajiv Porayath,Member, IEEE.A Robust Echo Canceler for Acoustic Environments [J].IEEE transactions on circuits an-d systems-II:analog and digital signal processing,1997,44(5):389-396.