DSP 对电子系统设计来说非常重要，因为它们能够迅速测量、过滤或压缩即时模拟信号。这样有助于实现数字电路和模拟电路之间的通信。但随着电子系统进一步精细化，需要处理多种模拟信号源，迫使工程师不得不做出艰难决策。是使用多个 DSP 并将其功能与系统的其余部分同步更具优势？还是采用一个能够处理多项功能的高性能 DSP 并配套精细的软件更具优势？

由于当今的系统非常复杂，在许多情况下单个 DSP 实现方案根本没有足够的处理能力。同时，系统架构也不能满足多芯片系统带来的成本、复杂性和功耗要求。

FPGA 已成为需要高性能 DSP 功能的系统的理想选择。事实上，与单独的数字信号处理器相比，FPGA 技术能够为高难度的 DSP 问题提供大为简化的解决方案。要明白其中的缘由，需要回顾一下 DSP 的肇始和发展。

用于实现专门目的的微处理器

在过去二十年里，传统的 DSP 架构一直在竭尽全力跟上不断提高的性能需求步伐。但随着视频系统大踏步地迈进高清和 3D 时代，通信系统为实现更高带宽已将现有技术发挥到极致，设计人员需要替代性实现策略。常用于实现数字信号处理算法的硬件不外乎如下三类基本器件之一：微处理器、逻辑和存储器。部分设计还需要额外的硬件来实现模数 (A/D) 和数模 (D/A) 转换以及高速数字接口。

传统的数字信号处理器是设计用于实现专门目的的微处理器，非常适合算法密集的任务，但性能受时钟速率及其内部设计的有序性的限制，从而限制了它们对输入的数据采样每秒最多执行的运算次数。一般来说，算术逻辑单元 (ALU) 运算一次需要三或四个时钟周期。多核架构可以提升性能，但提升的幅度仍有限。因此，采用传统的信号处理器设计必须将架构元件重复用于算法实现。对每次执行的加、乘、减或其它任何基本运算，每次运算都必须循环通过 ALU，不管是内部还是外部反馈。

但令人遗憾的是，在处理当今众多的高性能应用时，这种传统的 DSP 难以满足系统的要求。为此在过去已经提出过多种解决方案，其中包括在一个器件中使用多个ALU，或在一个开发板上布置多个 DSP 器件。但是，这些方案往往会造成成本大幅上升，同时把问题直接推向另一个领域。例如，用多个器件提高性能遵循指数曲线。要让性能提高一倍，需要两个器件。再提高一倍，则需要四个器件，依此类推。另外，编程人员的工作重点也从注重信号处理功能转为多个处理器与内核之间的任务调度。这样会产生大量额外的代码，而且这些代码会成为系统开销，而非用于解决眼前的数字信号处理问题。

FPGA 技术的引入是解决 DSP 实现方案日益增长的复杂性的福音。FPGA 最初开发用于整合和集中分立的存储器和逻辑，以实现更高的集成度、更出色的性能以及更高的灵活性。FPGA 技术已成为当今使用的几乎每一款高性能系统的重要组成部分。与传统的 DSP 相比，FPGA 是由可配置逻辑块 (CLB)、存储器、DSP Slice 及一些其它元件组成的统一阵列所构成的巨大并行结构。它们既可以使用VHDL 和 Verilog 等高级描述语言进行编程，也可以在方框图中用系统生成器 (System Generator) 编程。FPGA 还提供众多专用功能和 IP 核，可用于用高度优化的方式直接完成实现方案。

在 FPGA 中完成数字信号处理的主要优势在于能够根据系统要求定制实现方案。这就意味着对于多通道或高速系统，用户可以充分利用 FPGA 器件的并行性来最大化性能，而对低速系统，则可以更多采用串行方式完成设计。这样，设计人员就能够根据算法和系统的要求来定制实现方案，不必折衷理想的设计来迎合纯顺序器件的诸多局限。另外超高速 I/O 通过最大限度地提高从采集、处理到最终输出的数据流，可进一步降低成本并减少瓶颈问题。

如何比对 FPGA 的，下面以一个同时使用传统 DSP 架构和 FPGA 架构的 FIR 滤波器实现方案为例，来说明每种架构的优劣。

有限脉冲响应 (FIR) 滤波器是使用最广的数字信号处理元件之一。设计人员可用滤波器来改变数字信号的幅度或频谱，通常用于隔离或衰减样本数据频谱中的特定区域。从这个角度说，可以把滤波器视为信号的预处理方式。在典型的滤波器应用中，输入的数据样本通过精心同步的数学运算与滤波器系数相结合，不过这取决于滤波器的类型和实现策略，随后数据样本进入下一个处理阶段。如果数据源和终点都是模拟信号，则数据样本必须首先通过 A/D 转换器，结果则必须馈通给 D/A 转换器。

最简单的 FIR 滤波器的构造采用一系列延迟元件、乘法器和加法器树或加法器链来实现。

下面的等式是单通道 FIR 滤波器的数学表达：

该等式中的各项代表着输入样本、输出样本和系数。假设 S 为连续输入样本流，Y 为经滤波后产生的输出样本流，n 和 k 对应特定的瞬时时间。则如果要计算时间 n 时的输出样本 Y(n)，需要在 N 各时间点的样本群组，即S(n)、S(n-1)、s(n-2)…s(n-N+1)。N 输入样本群组乘以 N系数，加总后得出最终结果 Y。

在选择滤波器的理想长度和系数值时，有多种设计工具可供使用。其目的是通过选择适当的参数来实现所需的滤波器性能。参数选择最常用的设计工具是 MATLAB。一旦选定参数，就可以按照数学等式完成实现。

实现 FIR 滤波器的基本步骤包括：

1. 对输入的数据流采样

2. 在缓冲区组织输入样本，以便让每个采集到的样本与每项滤波器系数相乘

3. 让每个数据样本与每项系数相乘，并累加结果

4. 输出滤波结果。

使用“相乘累加法”在处理器上实现 FIR 滤波器的典型 C 语言程序，如下列代码所示：

/**采集输入的数据样本*/ datasample = input();

/**将新数据样本导入缓冲器*/ S[n] = datasample;

/**将每个数据样本与每项系数相乘并累加结果*/

y = 0;

for (i = 0; i {

y += k[i] * S[(n + i) %N];

}

n = (n+1) %N;

/** 输出滤波结 */ output(y);

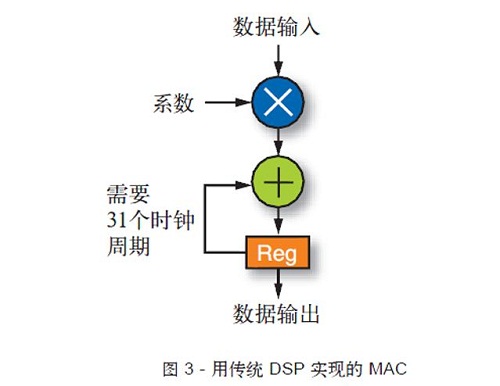
图 3 所示的实现方案被称为相乘累加或 MAC 型实现方案。这基本上就是用传统的 DSP 处理器实现滤波器的方法。采用内核时钟速率为 1.2GHz 的典型 DSP 处理器实现的 31 抽头 FIR 滤波器的最高性能约为 9.68 MHz，即最大的输入数据率为 968 Msps。

而 FPGA 提供了许多不同的设计和优化选择。如果需要高资源效率的设计，MAC 引擎法相当理想。这里还是以31抽头滤波器为例来说明滤波器规范对所需逻辑资源的影响。这种实现方案的方框图如图 4 所示。

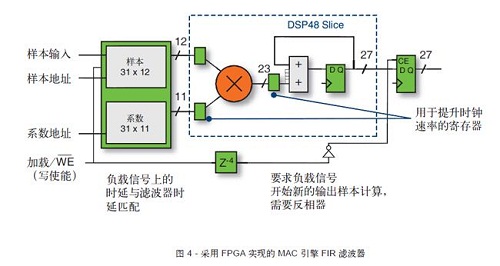
这种设计需要存储器存储数据和系数，可以混合采用FPGA 内部的 RAM 和 ROM。RAM 用于存储数据样本，故采用循环式RAM缓冲器来实现。字的数量与滤波器抽头数相等，位宽按样本大小设置。ROM 用于存储系数。在最糟糕的情况下字的数量与滤波器抽头的数量相等，但如果存在对称，则可以减少字的数量。位宽必须足以支持最大的系数。由于数据样本和系数数据随每个周期改变，故需要全乘法器。累加器负责将产生的结果累加起来。因为随着滤波器采集数据，累加器的输出会随每个时钟周期改变，故需要采集寄存器。当全套 N 样本完成累加后，输出寄存器负责采集最终结果。

如果采用 MAC 模式，则 DSP48 非常适用，因为DSP48 Slice 内含输入寄存器、输出寄存器和加法器单元。实现 31 抽头 MAC 引擎需要一个 DSP48、一个18 KbBlock RAM 和 9 个逻辑 Slice。另外还需要一些 Slice 用于采样、系数地址生成和控制。如果 FPGA 内置有 600MHz的时钟，则在一个 -3 速度等级的赛灵思 7 系列器件中该滤波器能够以 19.35MHz 的输入采样速率运行，即1,935Msps。

如果系统规范要求更高性能的 FIR 滤波器，则可采用并行结构来实现。图 5 显示了 Direct Form Type I 实现方案的方框图。

Direct Form I 滤波器能够在 FPGA 中实现最高性能的设计。这种结构通常也称为收缩型 FIR 滤波器，它采用流水线和加法器链让 DSP48 Slice 发挥出最高性能。输入首先馈送到用作数据样本缓冲器的级联寄存器。每个寄存器随后向 DSP48 提供一个样本，随即乘以对应的系数。加法器链负责存储部分结果，然后顺序相加，得到最终结果。

这种设计无需外部逻辑支持滤波器，且该结构可扩展用于支持任意数量的系数。由于没有高扇出的输入信号，故这种结构能够实现最高性能。实现 31 抽头 FIR 滤波器仅需要 31 个 DSP48 Slice。如果 FPGA 内置有 600MHz 的时钟，则在一个 -3 速度等级的赛灵思 7 系列器件中该滤波器能够以 600MHz 的输入采样速率运行，即 600Msps。

从这个实例可以清晰地看出 FPGA 不仅在性能上显著超越了传统的数字信号处理器，而且要求的时钟速率也显著降低（因此功耗也显著降低）。

这个实例只反映出采用 PFGA 实现 FIR 滤波器的部分技巧。为充分利用数据采样率规范，可对该器件进行进一步的定制，此时数据采样率可在顺序 MAC 运算极值和完全并行运算极值之间任取。用户还可考虑在涉及对称系数、内插、抽取、多通道或多速率的性能和资源利用方面进行更多权衡取舍。赛灵思 CORE Generator? 或System Generator 实用工具可帮助用户充分发掘这些设计变量和技巧。

在传统 DSP 和 FPGA 之间决策

传统数字处理器已经有多年的应用历史，当然不乏为特定问题提供最佳解决方案的实例。如果系统采样率低于数 KHz 且为单通道设计，DSP 可能是不二之选。但是，当采样率增加到数 MHz 以上，或者系统要求多通道，FPGA 就越来越具优势。在高数据速率条件下，DSP 只能勉为其能地在不造成任何损耗的情况下采集、处理和输出数据。这是因为在处理器中存在大量共享的资源、总线，乃至内核。而 FPGA 能够为每项功能提供专门的资源。

DSP 是基于指令而非时钟的器件。一般来说，对单个样本上的任何数学运算需要三条或四条指令。数据必须经输入端采集，发送到处理内核，每完成一次运算需循环通过内核，然后发送到输出端。相比之下，FPGA 基于时钟，故每个时钟周期都有可能在输入数据流上进行一次数学运算。

由于 DSP 的运算以指令或代码为基础，编程机制为标准的 C 语言，或者在需要更高性能的情况下，用低级汇编语言。这种代码可能包含高级决策树或者分支运算，难以在 FPGA 中实现。例如现存的大量用于执行预设功能或标准的代码，比如音频和语音编解码器。

FPGA 厂商和第三方合作伙伴已经意识到将 FPGA 用于高性能 DSP 系统的优势。如今已有许多 IP 核广泛应用于视频、图像处理、通信、汽车、医疗和军用等大部分垂直应用市场。与把高级系统方框图映射成为 C 语言代码的DSP 设计相比，将高级系统方框图分解为 FPGA 模块和 IP核会更加简便易行。

从 DSP 转向 FPGA

考查一些主要标准有利于在传统 DSP 和 FPGA 之间做出决策（见表 1）。

软件编程人员的数量远远超过硬件设计人员的数量，这已是不争的事实。DSP 编程人员的数量与 FPGA 设计人员的数量之间的关系也是如此。不过让系统架构师或者 DSP设计人员转为使用 FPGA 的难度并不像让软件编程人员转为从事硬件设计那么大。有大量的资源可以显著简化 DSP算法开发和 FPGA 设计工作。

主要的障碍是转换问题描述和解决的思路，即从基于样本和事件的方法转向基于时钟的方法。如果能够在设计流程的系统架构和定义阶段就能够完成，对这种转换的理解和应用就会简单得多。由彼此隔绝的不同工程师和数学专家负责系统架构的定义，DSP 算法的开发和 FPGA 的设计是司空见惯的事情。当然，如果每个成员对其他开发小组成员面临的难题有一定程度的认识的话，这个过程会顺利得多。

要支持 FPGA 实现方案，架构师不需要高度精通 FPGA 设计。只需要对器件、资源和工具有基本的理解即可。通过提供的多种专题课程，可以快速进阶。

具体的进阶方式取决于工程师的背景和专业知识。具体就 DSP 类课程而言，就有算法开发课、高效设计课和System Generator 设计课。如果用户期望成为在 FPGA 进行 DSP 设计的高手，Hardent 和其他赛灵思授权培训合作伙伴提供的三大课程可帮助您快速入门：DSP 入门、使用赛灵思 FPGA 完成 DSP 设计的必备技巧、使用 System Generator 进行 DSP 设计。

Hardent 还提供介绍赛灵思器件、HDL 设计入门语言、优化技巧，以及设计与调试策略的公共课。另外还有专门针对高速 I/O 设计、嵌入式处理和 DSP 设计技巧的专业课程和研讨会。