1.引言

如今，数字控制器被广泛应用于闭环控制系统中，如自动飞机着陆系统，伺服电机的运动控制以及机械手控制系统等。若数字控制器的采样率较高，闭环控制系统可视为连续体系。在高精度运动的数字控制器中，采样率是固定的并可能低至1kHz.如果设置控制器的参数采样率过低，那么闭环控制系统可能会变得不稳定，从而导致振动。

在振动抑制方面，很多学者将振动的抑制策略主要从控制方法角度考虑，这是由于系统中的不确定性、非线性等因素影响而使控制器在控制过程中振动抑制性能下降所致。针对伺服系统的振动问题，国内专家学者们提出了很多抑制方法，如PI/PID控制，IIR滤波器控制[5]和加速度观测器[6]等。

本文在分析闭环控制系统稳定性的基础之上，提出了低采样率控制系统的振动抑制方法，该方案与PI控制器结合使用，构成了一个振动补偿器。本文对闭环系统的稳定性和提出的振动抑制方案进行了研究，并通过MATLAB仿真平台验证了该方案的有效性。

2.控制系统的稳定性分析

考虑一个稳定的线性系统：

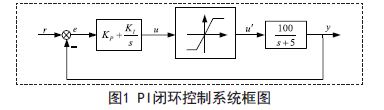
图1表示PI闭环控制系统，系统模型是一阶系统。该闭环控制系统的采样周期为h=0.001s.

PI控制器的参数是KP=30和KI=30.PI闭环控制系统的传递函数G(s)可以写成：

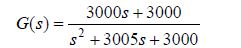
根据上式计算出G(s)的特征值：λ1 = ?3004,λ2 = ?0.9987.PI控制器的采样周期为h=0.001s,这会引起系统的不稳定。由于控制系统存在饱和项，故会产生振动，从而降低系统的性能.

3.振动补偿器的设计

图2是含振动补偿的PI控制器的控制框图。在图2中，e代表输入信号，u表示PI控制器的输出信号，KP、KI分别为PI控制器的比例系数和积分系数，Ks是增益的最大值，Ka是自适应增益参数，它决定了补偿策略的收敛速率。h是提出的策略的补偿信号。在图2中，振动抑制策略包含了一个死区功能。当u > e Ks 或u < e Ks ,h就非零。如果u的大小超出e与Ks乘积的绝对值，h就用来抵消e,从而使得u保持在上限内。

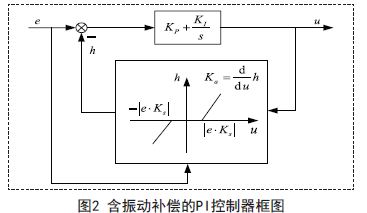
输出信号u和补偿信号h的关系：

值得注意的是，式(4)、(5)、(6)和(7)只有在u > e Ks 或u < e Ks 时成立。如果Ka设计得足够大，输入信号e和输出信号u的关系就可以被Ks所代替。换句话说，含振动补偿的PI控制器可以等价于增益K,而不需考虑赋给PI控制器的参数值.

图2中，PI控制器的采样周期是h=0.001s,为了使式(3)的系统达到稳定，增益K满足：

K<19.95 (8)

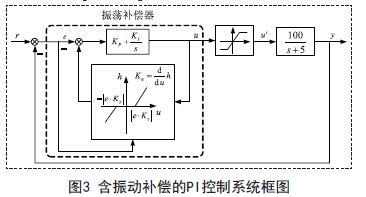
图3是含振动补偿策略的PI控制系统框图，根据式(7)和(8)，振动抑制策略的参数被设计为：Ks=15和Ka.

4.仿真结果

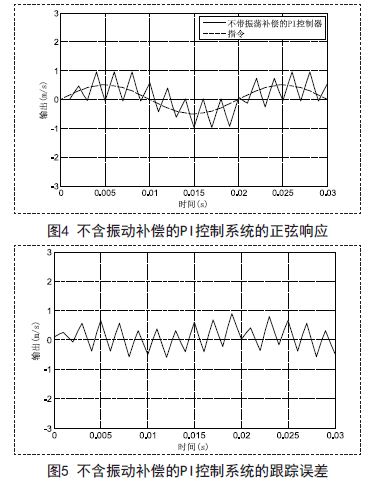
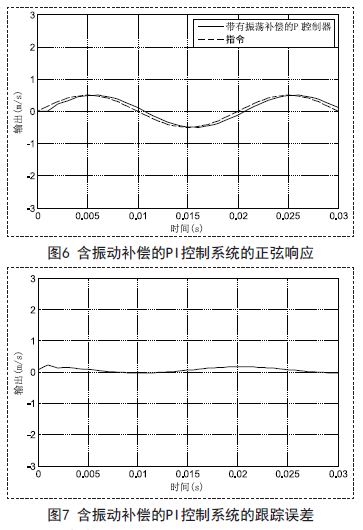
仿真结果将不含振动抑制方案的PI控制系统的正弦响应与含振动抑制方案的PI控制系统的正弦响应进行比较。仿真中，PI控制器的参数为：KP=30和KI=30.指令为：r = sin(100π t)m/ s.

PI控制器的采样周期为h=0.001s.将图4与图6对比看出，含振动补偿的PI控制器可以抑制振动。将图5与图7对比看出，含振动补偿的PI控制器系统的跟踪误差几乎收敛于零。仿真结果显示，在低采样率控制系统中，振动补偿策略能很好的抑制振动。

5.结论

本文针对低采样率控制系统因摩擦和饱和等因素造成的振动，提出了一种基于低采样率控制系统的振动抑制设计方案。在对闭环系统进行稳定性分析的基础之上，将该方法与PI控制器结合使用，所构成的振动补偿器可以不考虑赋给PI控制器的参数值。仿真结果表明，本文提出的振动抑制方案能有效抑制控制系统的振动。