3.仿真实例
在ADS软件中构建如下电路:
<ignore_js_op>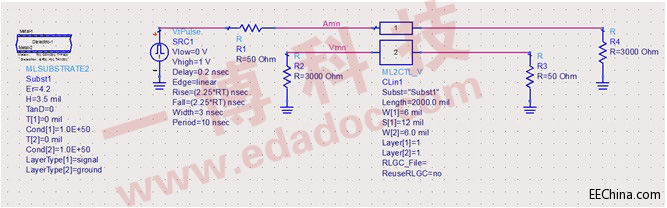
图2
图2为微带线的近端串扰仿真图,经过Allegro中的Transmission line Calculators软件对其叠板结构与线宽进行测试使其传输线的的特征阻抗为50ohm(见图3),并在在信号驱动侧串联50ohm的电阻消除源端反射,在负载端(信号接收端)用3000ohm来表征其高输入阻抗的特性。
<ignore_js_op>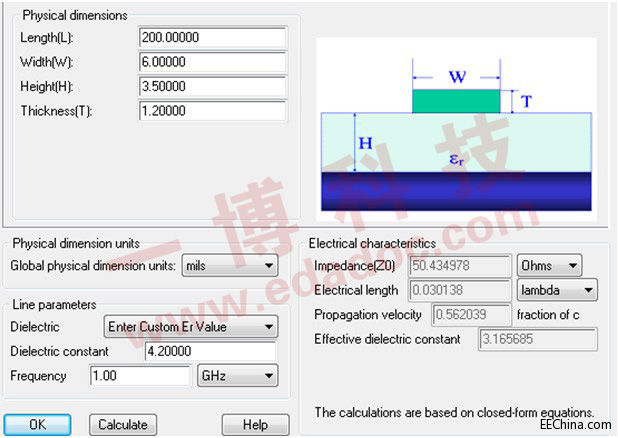
图3:微带线线宽为6mil,电解质常数为4.2,介质高度为3.5mil。
<ignore_js_op>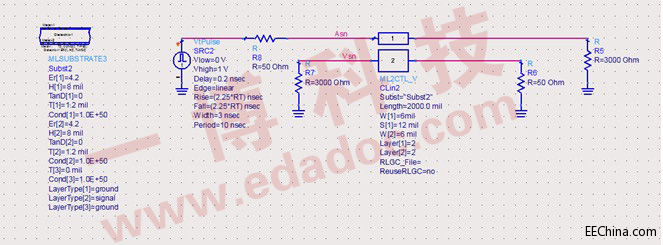
图4
图4为带状线的近端串扰仿真图,经过Allegro中的Transmission line Calculators软件对其叠板结构与线宽进行测试使其传输线的的特征阻抗为50ohm(见图5),并在在信号驱动侧串联50ohm的电阻消除源端反射,在负载端(信号接收端)用3000ohm来表征其高输入阻抗的特性。
<ignore_js_op>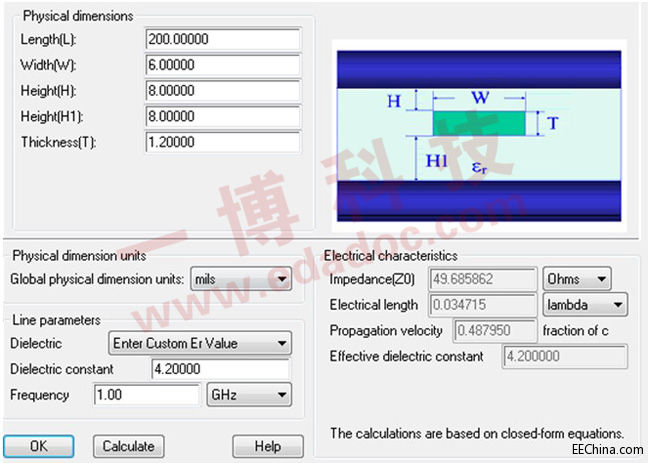
图5:带状线线宽为6mil,电解质常数为4.2,与两侧间距同为8mil。
<ignore_js_op>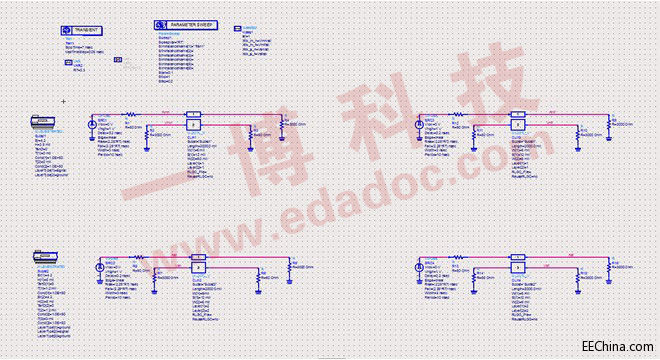
图6
图6中四个电路分别为微带线的近端串扰,微带线的远端串扰,带状线的近端串扰,带状线的远端串扰。红色为攻击线上信号,蓝色为静态线串扰。我们将线长定为2000mil,上升时间为RT (RT为信号从vlow-vhigh跳变20%-80%的时间,单位ns,整个vlow-vhigh跳变时间Rise=2.25*RT,本文中vlow=0V vhigh=1V),线宽都为6mil,线间距为12mil,满足3W原则。图7为当RT=0.3ns 各个电路的串扰图形。攻击线1V的驱动信号,受害线中微带线最大近端串扰为11mv,微带线最大远端串扰为12mv,带状线最大近端串扰为20mv,带状线最大远端串扰为20mv。
<ignore_js_op>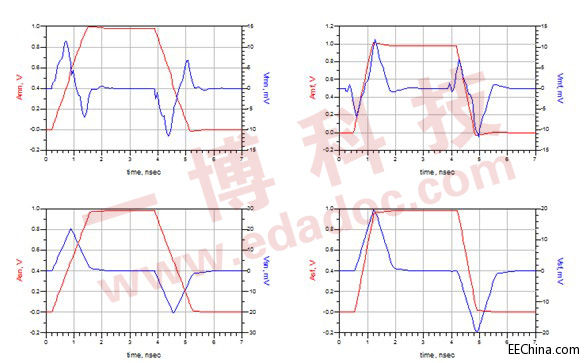
图7
我们以RT为变量,从RT=0.1ns到RT=1ns对电路进行仿真。结果如图8:
<ignore_js_op>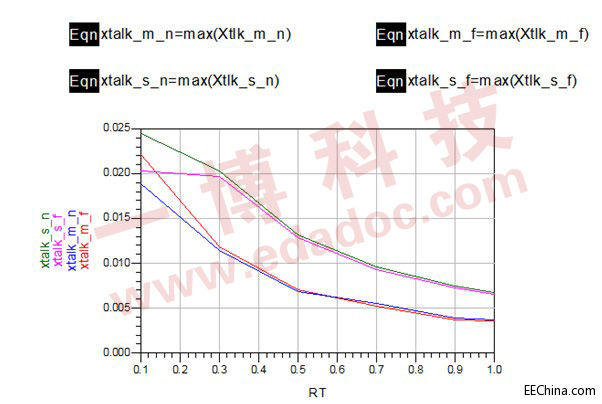
图8
Xtalk_m_n为微带线的近端串扰与输出电压的比值的最大值,Xtalk_m_f为微带线的远端串扰与输出电压的比值的最大值,Xtalk_s_n为带状线的近端串扰与输出电压的比值的最大值,Xtalk_s_f为带状线的近端串扰与输出电压的比值的最大值,其中带状线的串扰较大,但是当上升时间为0.1nsec时串扰最大也不超过2.5%,说明3W原则的实用性。
现在我们将其线宽不变,线距变成6mil,不满足3W规则,同样我们以RT为变量,从RT=0.1ns到RT=1ns对电路进行仿真。结果如图9:
<ignore_js_op>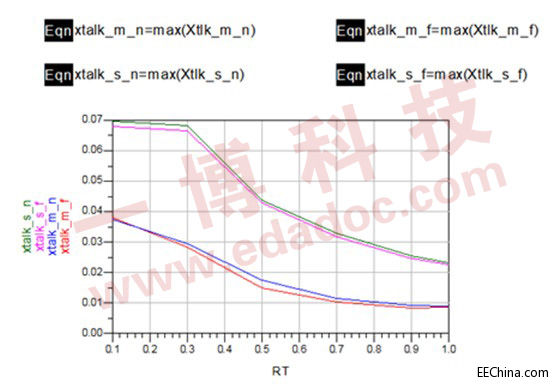
图9
从图上看出传输线上的串扰明显变大,但上升时间在1nsec时串扰同样低于3%。
传输线上的串扰不止跟上升时间与线间距有关系,与线长同样有关系。我们让RT=0.3ns,线宽为6mil,线距同样为6mil,以线长为L mil,以L为变量,从L=1000mil到L=3000mil对其仿真,结果如下(图10):
<ignore_js_op>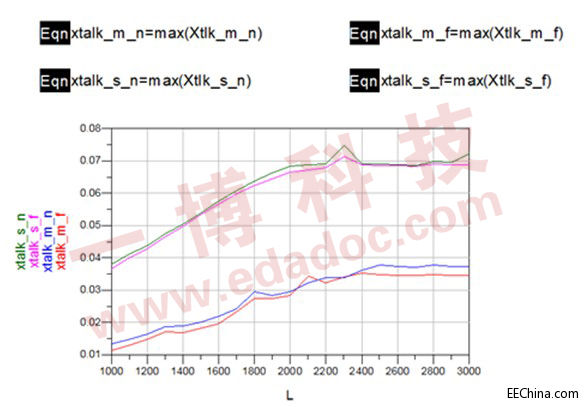
图10
由图10可知传输线的长度对信号的串扰影响也是非常大的,并且有饱和现象。
<ignore_js_op>
图11
图11为RT=0.3ns,L=2000mil,线间距从3mil变化至12mil时串扰的变化。
4. 结论
在实际的工程操作中,高速信号线一般很难调节其信号的上升时间,为了减少串扰,我们应该尽量满足3W原则,当然如果能约束布线的长度,很多时候会更容易满足信号完整性的要求。以下的结论基于源端匹配比较好,接收端阻抗较大的情况。
1.带状线在线宽与线距相等时,饱和时串扰率约为7%。
2.微带线在线宽与间距相等时,饱和时串扰率约为4%。
3.两线之间中心距变成x倍,串扰率变成1⁄x^2 。
4.饱和长度约为RT*v。在饱和长度之前,有(串扰率)/(饱和时串扰率)=(耦合长度L)/(RT*v)。
5.同组信号的串扰叠加在上升/下降沿上,影响较小。不同组信号的串扰可能造成信号的振铃等,影响较大。
6.时钟信号对串扰较为敏感,高速串行信号的时钟通常合并在信号中一起发送,串扰引起的抖动对接收的信号影响非常大,要特别注意。
以上的结论为一个量化估值,具体情况需要具体分析,不同信号对于串扰的敏感程度不一样,实际的上升时间也需要根据模型来定,除了靠经验之外,仿真也能帮助我们更精确的判断串扰。