摘要：本论文根据城市出租车运营的特点，在出租车监控平台数据的基础上，研究出租车投放数量调控的措施。出租车空驶率这一重要参数，可以根据采集的出租车运营信息计算得出，以此来分析乘客需求和运营效益与空驶率之间的关系，构建出租车运营模型，为完善出租车运营机制提供策略支持。

关键词：出租车；空驶率；数学模型；运量投放模型

近年来，随着经济的快速发展和人们生活水平的不断提高，居民对出行的效率和舒适程度提出了更高的要求，出租车以其高效、快速、便捷、安全的特点越来越受到人们的青睐。因此，出租车已经成为公共交通的重要补充。由于城市规模和人口的不断扩大，交通需求逐年提高，出租车的运营管理也面临着很大的挑战。如何调控出租车的投放数量，成为运营过程中很重要的环节，投放数量过少，供小于求，必然造成市民打车困难，出行不便。而投放量过多，同样也会造成出租车运营成本增加，导致城市交通拥堵，市民出行成本增加。因此，如何在出租车投放上全面兼顾乘客利益(即出租车运价和平均等待时间)和运营效益(运营成本和司机工资)，制定出合理的出租车投放策略，对于缓解城市交通的供求关系矛盾、优化交通环境和改善人民出行质量等方面都有重要意义。

1 研究内容

本论文的研究内容如下：

1)分析出租车行业运营现状，模拟出其运营过程，探索出租车行业相关因子(运价，司机工资，出租车公司收益等)之间的关系。

2)通过定性逻辑分析和定量挖掘分析，将与出租汽车行业相关的因素独立分析，将影响出租汽车行业的因素相互关联，建立相关数学模型。分为静态模型与动态模型两类，静态模型确定趋势，动态模型进行调控。

3)借助出租车运营的时间变化模型，根据得到的采样信息，提供投放调控措施，控制出租车的平均空驶率，提高出租车的工作效率，降低运营成本。

2 模型建立

出租车的运营收入与运营成本是分不开。作为乘客，必然是希望以最短的时间打到车并且付出较少的费用，然而作为出租车的经营方，也希望获得最大的利润，降低每一辆车的投入成本，作为出租车司机，希望获取更高的工资。出租车运营模型的研究需要综合以上多方面的因素，主要解决乘客需求与运营效用之间的矛盾。

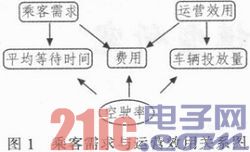
乘客的需求水平是一种不能数字化表示的抽象描述，如何将其与运营成本关联起来，就要使用一个非常重要的数据指标——空驶率，空驶率从一定角度反映了乘客对出租车的需求程度，空驶率越小，乘客的需求越大，同时空驶率也和乘客乘车的平均等待时间嘲有一定的关系。同样运营效用也与空驶率有一定的关系，在投放数量和运价等条件不变的情况下，空驶率越大，资源的浪费越大，运营收益越小。所以，空驶率作为一个可测量的参数，是出租车的运营投放模型的核心。其间关系如图1所示。

2．1 空驶率的计算

记录出租汽车运行信息，确定了每辆监测出租汽车上下乘客的位置和时间，据此可得到出租车交通运行特点的数据，为出租车运营模型研究提供数据支撑和事实依据。

对100辆出租车的运营情况进行采样调查。可以得出所有监测出租车在一个周期T(一天)内的的平均空驶率N，也可以得出在某个时刻t所有车辆的空驶率N(t)。

2．2 运营平衡方程

出租车运营平衡方程用来表示出租车运营收支相抵，将所有因素的复杂联系转换为收支平衡的关系。即

E=W (1)

左边E表示乘客乘车所花费的费用总和，右边W表示出租车的成本。其中W包含了出租车的损耗和维修费用Wl，燃油费用Wp，出租车司机的工资Wd，以及出租车公司的管理费Wa。则公式变为：

E=Wl+Wp+Wd+Wa (2)

为了将乘客需求和出租车的运营成本关联起来，在运营平衡方程中引入平均空驶率N这一参数，此时需要用到一些变量，其主要符号约定如下表1所示。

2．2．1 静态方程

由于车辆实际运营的情况十分复杂，我们也不可能把所有的因素都全部考虑到，所以对出租车辆的运营过程做了简化，忽略了起步价的环节，对车辆的载客行驶速度和非载客行驶速度取了平均值Vp和Vn。为了方便建立模型，对于车辆的损耗，维修和保险费用，出租车司机的工资以及出租车公司的管理费用都取了统一的度量单位。在此条件的下，一个T时间周期内的出租车辆运营情况可表示为：

根据式(3)和(4)，取统一时间周期，约去T后得：

式(7)反应了出租车运价和其他因素之间的关系，在空驶率不变的情况下，运价f和出租车运营损耗Lt，出租车司机工资Dt和出租车公司管理费用Wt是呈线性关系，同样有效的控制载客和非载客行驶速度也能降低运价。

然而实际中车辆的空驶率是一个随时变动的参数，其对乘客，司机，出租车公司的收益都有反馈作用。因此静态方程可用于确定各个参数的初始值，及分配比例，决定整体的趋势。

2．2．2 动态方程

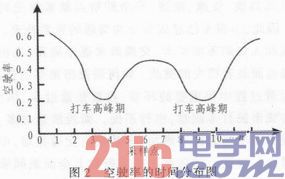
然静态方程可以描述出出租车运营的宏观状况，但是为了对一天内每一时刻的运营状况进行分析，还需要动态方程。根据出租车运营空驶率随时间变动的规律，我们可以对每天相应时间段的车辆运营信息进行采集，得出出租车在一天内的运营空驶率随时间分布。如图2所示。

对出租车运营信息定时采样可以得出N(t)，t=0，1，2，3，4…，则式(5)引入随时间变化的参数N(t)，变形为：

动态方程表现了各个采样时刻的车辆运营状态，针对其中一个参数进行分析，进行微观的调控。例如，在其他条件不变的情况下，当空驶率增加时，出租车的使用率会浪费，为保证原有的收支平衡，必须通过提高运价f来弥补损失。空驶在空驶率较小的时候，减少车辆的投放，降低运营成本，提高效率。准确获得每一个时刻的车辆的空驶率，可以帮助我们准确的制定出租车辆投放策略，我们希望空驶率始终保持在一个均衡的水平，理想状态下经过出租车投放调控，采样得到的车辆空驶率时间分布应该是一条水平直线或者是在一个较小区间内变化的曲线。

3 投放调控

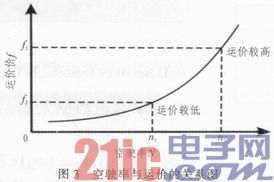
通过对出租车的样本运营信息进行采集，可以得到空驶率的时间分布曲线但是我们将空驶率控制在一个怎么的范围，需要进一步的讨论。将出租车运营损耗Lt，出租车司机工资Dt和出租车公司管理费用Wt都设为常数时，根据公式(7)，运价f与空驶率n的关系如图3所示。利用对不同人群的调查统计方法，我们可以得到绝大多数市民可以接受的运价区间[f1，f2]。由图3的关系曲线，算出一个空驶率区间[n1，n2]。

根据空驶率的区间[n1，n2]，和空驶率的时间分布图形，对车辆投放进行修正，空驶率低于n1时，应当加大车辆的投放，空驶率大于n2时则应当减少车辆的投放，使得空驶率时间分布曲线始终落在n1和n2之间。实现结果如图4所示。

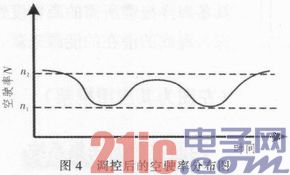
通过对出租车的投放控制，调节出租车辆的空驶率，使得出租车的运营始终保持在一个平衡的状态，既要保证乘客的经济承受能力，又能维持出租车的整体效率。

4 结束语

文中通过分析出租车运营中各个因素的关系，以空驶率为核心参数，尽量将出租车运营中主要因素全部包含在一个模型中，建立了运营平衡模型，并对每一个因素的变化进行分析，提出了出租车辆的投放策略和调控的方向，并对控制方法进行了数字化处理。本文对于运价的起步价没有进行处理，这使得模型相对简单，也是后续的一个改进方向。