传统FFT利用三角函数的正交性，将信号分离出来，从而将时域的信号变换到频域。但是，它有一个很重要的前提：输入的序列必须是周期内等间隔采样的值，这样，FFT计算的结果才是我们想要的。传统FFT的结果可以通过一些算法实现频谱校正，如全能重心法、比值法等等。但都是基于FFT的结果，精度有限。全相位FFT算法是天津大学的王兆华和候正信教授提出的，具有初始相位不变和有效防止频谱泄露的特性，并有相应的matlab程序。对于apFFT 的理论研究已有一些论文，但是硬件实现此算法的研究还很少见。本文对此新型频谱分析算法用FPGA来实现，并进行了仿真和分析。

目前，通常采用两种途径通过硬件方式实现FFT算法：（1）使用DSP器件实现；（2）通过FPGA器件实现。一般来说，DSP器件多用于数字信号处理领域，而且开发过程相对简单，易于实现，但速度较慢，无法完成对速度要求较高的算法。而FPGA器件由于内部嵌入了硬件乘法器、可编程寄存器和M4K内存块，在速度上具有明显的优势。考虑到apFFT对速度要求较高，故选用FPGA器件作为硬件开发平台。

1 全相位频谱分析

FFT（FastFourier Transformation），即为快速傅氏变换，是离散傅氏变换的快速算法，它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。它对傅氏变换的理论并没有新的发现，但是对于在计算机系统或者说数字系统中应用离散傅立叶变换，可以说是进了一大步。

apFFT理论推导详见参考文献,本文以FFT点数N=3点为例简化此频谱分析图如图1.其中的卷积窗wc=[wc（-N+1），…， wc（-1）， wc（0）， wc（1），…， wc（N-1） ] 由两个长度为N的对称窗卷积而来，用这个长为（2N-1）的卷积窗wc 对输入样本加窗后，再将间隔为N的两数据平移相加生成N个数据y（n） （n=0,1,…，N-1），最后对y（n）进行FFT 即得谱分析结果。

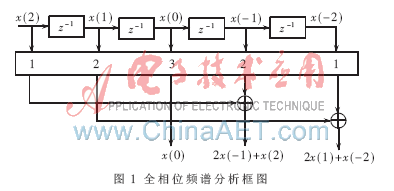
2 软硬件简介

在FPGA开发过程中，常用的是VHDL和Verilog HDL语言。VHDL语言比较适合做大型的系统级设计，而Verilog HDL则适合逻辑级、门级设计。所以，考虑到两种语言各自特点，本文选用VHDL语言完成设计。

采用FPGA实现apFFT算法，对硬件资源要求较高，故开发芯片选择Altera公司的EP2C35F672C8.该芯片内部包含有33 216个逻辑单元，105个M4K RAM模块，以及18 bit×18 bit嵌入式乘法器。

软件选用Altera公司开发的QuartusII平台。该软件提供了丰富的开发工具供用户使用，可以完成代码输入、编译、仿真以及下载到芯片的全部功能。

3 apFFT模块设计

本文所设计的apFFT模块由三部分构成，分别为：地址发生模块、数据存储模块和FFT运算模块。各个模块间的关系如图2所示。

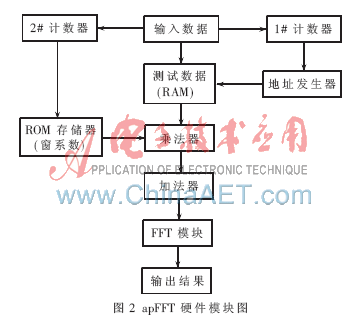
3.1 地址发生模块

为了保证测试数据能够完整无误地输入到EP2C35F672C8,需要选择合适的存储地址来保存数据。本文以做8点FFT为例，所涉及的所有数据总线宽度均为8 bit,序列长度取15 bit.为了保证15 bit的存储数据都能够及时存储到寄存器中，需要至少4 bit的地址总线才能满足设计需求。

地址发生模块的结构体部分程序如图3所示。

编译通过之后，得到的Symbol文件如图4所示。

3.2存储器设计

存储器（Memory）是计算机系统中的记忆设备，用来存放程序和数据。计算机中全部信息，包括输入的原始数据、计算机程序、中间运行结果和最终运行结果都保存在存储器中。它根据控制器指定的位置存入和取出信息。有了存储器，计算机才有记忆功能，才能保证正常工作。按用途存储器可分为主存储器（内存）和辅助存储器（外存），也有分为外部存储器和内部存储器的分类方法。外存通常是磁性介质或光盘等，能长期保存信息。内存指主板上的存储部件，用来存放当前正在执行的数据和程序，但仅用于暂时存放程序和数据，关闭电源或断电，数据会丢失。

3.2.1 数据存储器

由于输入数据由总线宽度为8 bit的实部和虚部两部分构成，所以需要双口RAM对数据进行存储。这样设计的优势在于能够很好地将输入数据按其顺序输入到FFT核当中，而且方便对不同地址的数据进行实时调用。

在对模块设计过程中，可以直接调用QuratusII里的MegaWizard Plus-In Manager工具定制RAM.定制过程中，需要对RAM的控制线、地址线和数据线进行选择，这里选择地址线宽度为4 bit,输入、输出数据线宽度为8 bit,读取时钟信号rdclock同时控制读地址和RAM的输出。

在该存储器中，时钟信号wrclock和rdclock分别控制随机存储器的写、读状态，均为高电平有效。同时，wrclock和rdclock作为写、读数据的地址发生器工作。即对wrclock和rdclock的上升沿进行计数，并根据计数结果产生相应的地址位。生成的数据存储器如图5所示。

需要注意的是，由于EP2C35F672C8属于CycloneII器件，在调用RAM模块时，必须做如下设置：选择Assignments→Setting命令，在弹出的对话框中选择Analysis & Synthesis Settings下的Default Parameters选项，并在该选项的Name文本框中输入CYCLONEII_SAFE_WRITE;在Default Setting文本框中输入VERIFIED_SAFE,并分别点击Add和OK按钮关闭Settings窗口。这样才能在最后综合以及仿真时，得到正确的结果。

3.2.2 窗函数存储器

apFFT相比传统FFT,最大的区别在于其FFT运算模块输入数据是经过预处理的数据，而非采集电路直接采集到的数据。在进行数据预处理的过程中， 非常重要的部分就是窗系数的选择。以N=8点FFT为例， 全相位输入数据是2N-1=15个， 采集余弦函数的15个数据为： -0.173 65,-0.990 27,-0.438 37,0.719 34,0.882 95,-0.173 65,-0.990 27,-0.438 37,0.719 34,0.88 295,-0.173 65,-0.990 27,-0.438 37,0.719 34,0.882 95.

按照参考文献[1,2] 选择的窗函数为： 0.013 684, 0.096 665,0.346 18, 0.846 66, 1.590 8,2.431 7, 3.111 8,3.375,3.111 8,2.431 7,1.590 8,0.846 66,0.346 18,0.096 665,0.013 684.将窗函数转换为8 bit二进制的形式，并存储到只读存储器当中以方便运算。如图6所示。

将输入数据经加窗处理并叠加后，在matlab中得到的结果为：-1.479 5,2.236 1,2.051 3,-0.428 0,-0.229 4,1.252 9,-0.352 7,-3.069 4.此时， 在QuartusII中得到的结果为-1.236 8, 2.339 7, 2.004 9, -0.402 9, -0.180 3, 1.118 6,-0.348 5,-2.985 6.可以看出两者有一定的误差，其原因是在QuartusII中得到的结果是以二进制形式表示，在转换过程中存在一定的量化误差。

3.2.3量化误差

FPGA（Field-Programmable Gate Array），即现场可编程门阵列，它是在PAL、GAL、CPLD等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点。FPGA一般来说比ASIC（专用集成芯片）的速度要慢，无法完成复杂的设计，而且消耗更多的电能。但是他们也有很多的优点比如可以快速成品，可以被修改来改正程序中的错误和更便宜的造价。厂商也可能会提供便宜的但是编辑能力差的FPGA.因为这些芯片有比较差的可编辑能力，所以这些设计的开发是在普通的FPGA上完成的，然后将设计转移到一个类似于ASIC的芯片上。另外一种方法是用CPLD（复杂可编程逻辑器件备）。

在FPGA中实现算法，一般要对十进制的小数进行量化，即将十进制的小数转换为二进制数，并运用二进制补码表示，兼顾舍入误差，由于将十进制小数转换为二进制比较繁琐，现编写matlab程序进行转换：下面是将整数部分不为零的十进制的小数转换为二进制小数的部分程序：

function [num,numint,numf]=dectobin1（innum,N）；

%clc;clear;close all;

%十进制数转换为二进制数

%输入为十进制数innum,以及小数部分的位数N

%输出为三个参数num,numint,numf

%num为输出的二进制形式

%numint为整数部分的二进制表达式

%numf为小数部分的二进制表达式

sep=5;%整数和小数部分的分隔符

if（mod（innum,1）==0）%判断输入是否为整数，mod为取余函数

numint=dec2bin（innum）；

numint=double（numint）-48;

numf=zeros（1,N）；

num=[numint,sep,numf];

return

end;

%输入为非整数的情况

nint=floor（innum）；%整数部分

nf=innum-nint;%小数部分

res_nint=dec2bin（nint）；

res_nint=double（res_nint）-48;

res_nf=dectobin（nf,N）；

numint=res_nint;

numf=res_nf;

num=[numint,sep,numf];

在FPGA中只能进行定点运算，根据对系数的量化误差及有效字长效应，对加卷积窗的系数进行量化，所有的系数均采用二进制补码的形式表示，也就是采用有符号的八位二进制补码表示，在量化过程中，由于计算相对复杂，工作量比较大，如果采用手工计算来进行量化显然是不可取的，而且也容易出现错误，为此利用前面为量化误差编写的程序进行量化，这样大大减少了工作量，提高了工作效率。而且在设计中系数还具有线性相位的特性，利用这一特性更加减少计算的工作量。

对系数进行量化的数值如表1所示。

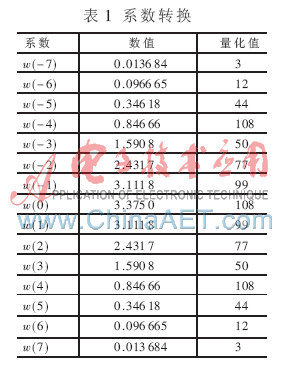
3.3 FFT运算模块

这里的FFT模块，可以通过两种方式得到。

第一种是自己编写一个FFT算法的子程序，编译通过后将该子程序打包成一个Symbol文件，并在最后的顶层文件中进行调用。这种方法的好处在于对FFT的算法能够很好表达，并根据需要进行灵活修改，缺点是开发周期较长，硬件资源利用率不是太高。

第二种设计方法是安装Altera公司提供的IP核，并对其进行相应的参数设定。这种开发方法的好处在于简单易用，并且能够很好利用硬件资源。缺点是由于该核包含知识产权，商用时需缴纳一定版权费用。考虑到本设计尚处于研究阶段，故选择后一种开发方式，也便于减少硬件资源的消耗。在使用IP核的过程中需要对FFT核的参数进行设置，过程分为三步：参数设定（Parameterize），仿真设定（Set Up simulation）以及产生FFT核（Generate）。

4 编译及仿真

对最终的顶层文件进行编译，并对其进行时序仿真。其仿真结果如图7所示。

在图7中，可看到最终仿真之后得到的波形情况，图中所有值均以二进制形式显示。

本设计所得到的硬件仿真结果与Matlab软件仿真得到的结果基本一致，说明apFFT的FPGA的可行性。下一步将对此设计进行改进，可以根据FFT点数实时地对apFFT模块进行参数化设置。

最终设计的FFT模块使用了2 755个逻辑单元，仅占硬件资源的8%.可见该设计的资源耗用与直接对数据进行FFT运算的资源耗用大体相当，apFFT和FFT计算效率分别是NlogN+2N和NlogN+N.因为apFFT相对于传统的FFT,虽然采样点数多了N-1,但最终都用一个N阶FFT实现，而计算量主要体现在FFT中。在不增加FFT点数情况下，硬件资源耗用没有明显增加，但相对于传统的FFT可以降低频谱泄露，并且用apFFT测相位不用任何校正，所以在后续开发做频谱分析或者相位计时计算量会很小，有利于实时实现。