神经网络是:思维学普遍认为,人类大脑的思维分为抽象(逻辑)思维、形象(直观)思维和灵感(顿悟)思维三种基本方式。逻辑性的思维是指根据逻辑规则进行推理的过程;它先将信息化成概念,并用符号表示,然后,根据符号运算按串行模式进行逻辑推理;这一过程可以写成串行的指令,让计算机执行。然而,直观性的思维是将分布式存储的信息综合起来,结果是忽然间产生想法或解决问题的办法。这种思维方式的根本之点在于以下两点:1.信息是通过神经元上的兴奋模式分布储在网络上;2.信息处理是通过神经元之间同时相互作用的动态过程来完成的。标准的神经网络VLSI的实现方式是在单个芯片上集成多个神经元和突触单元,并且将它们按某种通信结构组成神经网络 系统,此外,还有基于ASIC结构的,针对神经网络运算特点进行优化和简化设计的FPGA
实现方式,以及基于商业处理器(如数字信号处理、RISC单片处理等)的模拟神经网络的多处理器结构的实现方式。
衡量一个神经网络性能的重要指标是快速性和适用性,而FPGA的集成度已经达到百万门级,用FPGA构造神经网络时,可以灵活地实现各种运算功能和学习规 则,并且设计周期短、系统速度快、可靠性高、输入输出接口灵活、几乎可以和任何形式的并行、串行接口及并行、串行A/D或D/A,DSP等连接,同时由于 可以将整个系统都集成在单个芯片内,因而抗干扰性能极强,使其在自动控制、故障诊断、模式识别,图像获取、DSP应用、嵌人式系统等领域有着广泛的应用前 景。所以,FPGA无疑是首选的实现神经网络的硬件芯片。
1 BP神经网络的基本原理
BP(BackPropagation)网络是1986年由Rumelhart和McCelland为首的科学家小组提出,是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(outputlayer)。当有信息输入网络时,该信息首先由输入层传至隐含层节点,经特性函数作用后,再传至输出层输出,其间每经过一层 都要由相应的特性函数进行变换。节点的特性函数要求是可微的,通常选用S型函数,特性函数通常取Sigmoid函数,本系统选用Sigmoid函数,即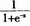 和
和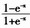 作为特性函数,具有较好的收敛性,模拟结论也比较符合实际情况。
作为特性函数,具有较好的收敛性,模拟结论也比较符合实际情况。
2 BP学习算法描述
BP网络中每个节点都有一个状态变量xi,节点i到节点j有一个连接权系数wji,每个节点都有一个阈值θj,每一个节点定义一个变换函数fj[xi,wji,θj(i≠j)],最常见的形式为
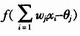
为了方便起见,将阈值θ作为神经元权值的第一个分量加到权值中去,那么输入向量就应增加一项,可设输入向量的第1个分量固定为l,这样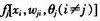 的形式就可变为
的形式就可变为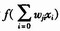 。
。
一个3层单输入、单输出、n个隐节点的BP网络结构如图l所示。
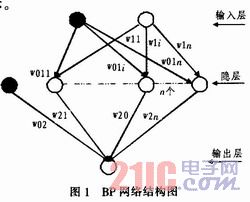
图1中,黑圆表示输入为固定值1的神经元,用它与隐层神经元的连接权w011~w01n来表示隐层神经元的阈值,它与输出层神经元的连接权w02来表示输 出层神经元的阈值,w1I~w1n为输入层到隐层之间的连接权值,w21~w2n为隐层到输出层之间的连接权值。描述一个如图1所示网络的BP算法,它主 要包括2个阶段:
1)正向传播阶段 从样本集中取出一个样本(x,d),计算隐层各个节点(神经元)输出yI(i)=f(wl(i)x-w01(i))和输出层节点输出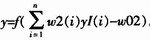 。
。
2)反向传播阶段 按下式反向计算各层节点的局部梯度δ和权值修正量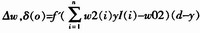 。
。
若激励函数f选用单极性Sigmoid函数,则:


式中,x是输入,d是期望输出,f为激励函数,η为学习率,δ(o)为输出层节点的梯度,δi为隐层节点i的梯度。
3 BP神经网络的VHDL设计
3.1 选择系统处理数据字长
在运算中,涉及大量乘累加操作,本应采用浮点运算,但是占用的硬件资源和速度都将会不理想;如果采用定点运算,运算中带来的"位增长"率将使每一级运算的 最大值可能会逐级加倍,因此如果不精心地规划设计,这些值就会溢出,结果会因为精度不够而无法使用。因此采用自定义的定点数进行基本的运算单元设计。本系 统采用不削弱神经网络能力的最小要求16位(1,5,lO)带符号定点数表示,最高位为符号位,低10位为小数位,其余为整数位。
例如:将1.5用16位(1,5,1O)带符号定点数可表示为:0000011000000000,将-2.3用16位(1,5,10)带符号定点数可表示为:10001 00100110011.
3.2 BP神经网络模块库的建立
根据文件复用性的要求,建立基于VHDL语言的BP神经网络元件库,根据层次设计的要求,BP神经网络结构的描述分为3层:第1层是前向 传输模块的描述,包括输入信号加权求和,权值的存储和非线性激励函数的实现;第2层是反向传输模块的描述;第3层是系统控制模块的描述。下面用VHDL语 言对这3层结构分别进行设计。
3. 2.1 前向传输模块的设计
图2为前向传输模块的VHDL程序设计流程。计算时x和w都是16位有符号数。相乘后为3l位数(最高位为符号位(两输入数符号位相异 或),低20位为小数位,其余10位为整数位),为了节省硬件资源四舍五入,舍去低10位小数位,为了防止后面相加是溢出,再扩展4位整数位,所以乘累加 后输出为25位。
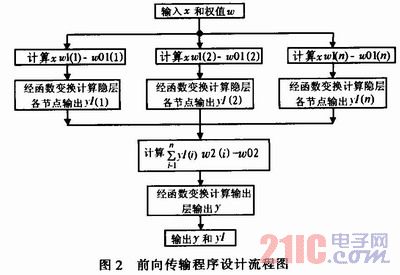
函数变换部分:对于FPGA硬件来说,其可实现的运算极为有限,而BP网络中的作用函数sigmoid函数是非线性的,是硬件实现的一个难点,常用的实现 方法是查表法,这种方法比较简单,但需要占用较多资源,当需要实现的网络规模较大且精度要求较高时,查表法的实现有很大障碍;还有一个方法就是多项式逼近 法。本系统使用了查表和多项式逼近2种方法。
3. 2.2 反向传输模块的设计
反向传输模块的VHDL程序设计流程如图3所示。
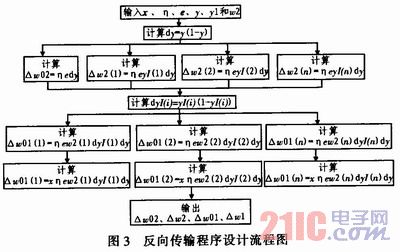
使用3输入的乘法器计算△w02,4输入的乘法器计算△w2.5输入的乘法器计算△w01,6输入的乘法器计算△w1,这样并行计算△w02、△w2、△wO1、△w1.
3.2.3 系统控制模块的设计
该系统控制模块由一个计数器组成,计数器的输入信号有:时钟信号、启动运算信号start、最大训练次数maxcount、误差信号e、 误差容限eps,样本数目;输出信号有:前向传输控制信号enl,求误差控制信号en2、反向传输控制信号en3、权值调整控制信号en4、权值读写信号 en5、读样本地址信号,训练次数count.
3.3 基于FPGA的芯片和仿真软件选型
FPGA(Field-Programmable Gate Array),即现场可编程门阵列,它是在PAL、GAL、CPLD等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。FPGA一般来说比ASIC(专用集成芯片)的速度要慢,无法完成复杂的设计,而且消耗更多的电能。但是他们也有很多的优点比如可以快速成品,可以被修改来改正程序中的错误和更便宜的造价。厂商也可能会提供便宜的但是编辑能力差的FPGA.因为这些芯片有比较差的可编辑能力,所以这些设计的开发是在普通的FPGA上完成的,然后将设计转移到一个类似于ASIC的芯片上。另外一种方法是用CPLD(复杂可编程逻辑器件备)。
芯片选型要考虑的因素有:硬件资源,例如LE个数、PLL个数、RAM个数;核心及外设电压标准、功耗;软件工具的功能对VHDL语言的支持;市场上专业开发板的支持。
本系统设计采用Altera公司Cyclonell系列的EP2C20Q240C8型FPGA.器件EP2C20Q240C8片内资源丰富,逻辑单元共18752个,最大用户输入输出引脚为142个,器件EP2C20Q240C8还内嵌RAM,共208 KB,包含4个PLL,同时支持Nios软核处理器。EP2C20Q240C8型FPGA的核心电压是1.2 V,I/O电压是3.3 V.而综合软件则使用Altera公司的QuallusⅡ6.1.
4 实验验证
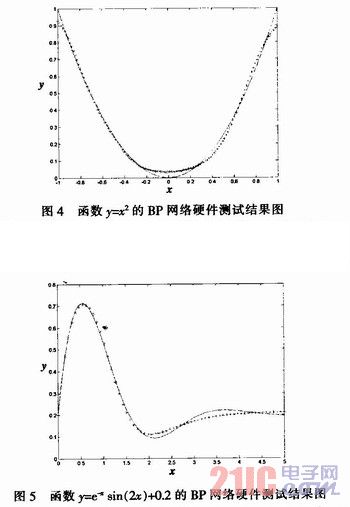
将该BP网络用来实现函数逼近,取网络为l-5-l(输入、输出层神经元数为1,隐层神经元数为5),本系统测试了很多函数,现将其中2例测试结果列出, 如图4所示,(图中实线为目标曲线,+线为逼近曲线)。由测试结果可以看出,对于函数中比较平坦的地方,该系统拟合结果不太理想,对于不同的网络结构,网 络模型的误差或性能和泛化能力也不一样,一般地,随着网络结构的变大,误差变小。通常,在隐层节点数增加的过程中,网络误差会出现迅速减小然后趋于稳定的 一个阶段,因此,合理的隐层节点数应取误差迅速减小后基本稳定时的隐层节点数。合理网络模型是必须在具有合理隐层节点数、训练时没有发生"过拟合"现象、 求得全局极小点和同时考虑网络结构复杂程度和误差大小的综合结果。设计合理的BP网络模型的过程是一个不断调整参数的过程,也是一个不断对比结果的过程, 比较复杂且有时还带有经验性。
例l:待测函数y=x2,测试结果如图4所示。
例2:待测函数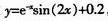 ,测试结果如图5所示。
,测试结果如图5所示。
5 结论
以BP网络为例提出了神经网络硬件实现方法。应该说明的是:这种方法并非只适合于BP网络,由于神经网络都具有大规模并行的简单运算的特点,所以可以将此方法推广至更多类型的神经网络。
本系统在参考前人工作的基础上,综合考虑了各种因素,用VHDL硬件描述语言设计并实现了该系统,从测试结果来看,本文所设计的BP神经网络不但达到了一 定的数据精度,也能满足一般场合下的速度处理要求。此尝试的成功将改变人工神经网络的研究局限于算法和应用等领域的现状,也必将极大促进神经网络研究的进 一步发展,这也将推动神经网络硬件在相关应用领域中的实用化。