摘要：分析了数字滤波器的原理，介绍了采用窗体函数法完成FIR数字滤波器，包括MATLAB仿真和DSP的实现方法。通过MATLAB仿真验证了所设计的滤波器具有良好的滤波功能，以TMS320F2812DSP为核心器件，用DSP控制器来实现FFT算法完成多点、实时控制。实验结果表明，该设计性能稳定、效果良好、实用性强。

关键词：FIR数字滤波器；MATLAB；DSP；FFT算法

随着计算机和信息技术的快速发展，数字信号处理技术在通信与电子技术、航空航天、仪器仪表等诸多领域得到了广泛应用，数字滤波器作为数字信号处理技术的一个重要工具，可用来过滤时间离散信号和数字信号。在数字信号处理中，数字滤波器占有极其重要的地位，滤波器可以用软件滤波或专用的硬件滤波两种方法实现。硬件滤波器稳定性差，易老化，精度低。用软件来实现数字滤波器的优点是随着滤波器参数的改变，很容易改变滤波器性能，从而满足设计需求。

本设计采用具有严格线性相位、稳定性好的FIR数字滤波器来实现滤波器的设计。MATLAB作为设计FIR滤波器的强有力工具，为设计应用提供了相应的工具箱，从而将复杂的程序设计简单化为函数调用，简化难度的同时还提高了效率。TMS320F2812DSP是TI公司推出的一款用于控制和数字信号处理领域的多功能、高性价比的芯片，其优良的性价比使其在数字信号的实时处理中得到了广泛的应用。本文介绍了采用MATLAB仿真技术和DSP来设计实现FIR数字滤波器。

1 数字滤波器原理

对于数字滤波器，描述系统特性用差分方程。设其输入序列为x(k)，输出序列为y(k)，则它们之间的关系可以用差分方程来表示：

y(k})+b1y(k-1)+…+bMy(k-M)=a0x(k)+a1x(k-1)+…+anx(k-N) (1)

其中，y(k)系数一般取1；b1，…bM及a0，…aN为常系数；

对于特定的系统，M和N为常数，分别代表输出最高阶数和输入最高阶数。

2 FIR数字滤波器设计方案

数字滤波器的设计有无限冲激响应滤波器(IIR)和有限冲激响应滤波器(FIR)两种选择。无限冲激响应滤波器的设计是借助模拟滤波器转换的设计方法，一般有公式和图表可查询，另外还有一些典型模拟滤波器可供选择，这种方法相对比较简单。有限冲激响应滤波器主要采用非递归结构，可以保证绝对的稳定，这有利于对谐波相位的分析。

在数字滤波器差分方程的基础上，如果全部ak=0(k=0，1，…，N)，此时系统的输出只和输入x(n-k)有关系，则以上公式成为没有反馈的递归结构。设FIR滤波器的单位冲激响应h(r)为一个N点有限长序列，其中0≤r≤N-1。

则FIR数字滤波器的传递函数可以表示为

从FIR数字滤波器传递函数表达式可以看出，其传递函数是一个Z-1的N-1次多项式，它在z平面上有N-1个零点，没有极点(有时认为在原点上有N-1个重极点)。其传递函数实际上就是单位抽样序列的z变换。

当数字滤波器的技术指标确定后，可以用一定的方法去逼近，目前FIR滤波器设计主要有3种方法：窗函数法、频率抽样法和切比雪夫最佳一致逼近法。

FIR滤波器的设计任务是根据给定的技术指标确定一个传递函数H(z)，使其频率响应满足给定的要求。这些方法设计出的滤波器特性都是在不同意义上对理想频率特性的逼近。

3 FIR数字滤波器的设计

若信号高频分量很小，信号大部分能量集中在低频处，那么谐波测量仪只要求测到20次谐波就可以了，截止频率为1 000 Hz左右，20次以上的谐波需要由滤波器滤除，为了达到更好的滤波效果，在硬件滤波的基础上又增加了数字滤波器。这里以有闭合公式可循的窗函数法为例来介绍FIR滤波器设计。

3．1 滤波系数确定方法

首先，各技术指标如下：

FIR滤波器的设计采用MATLAB数字信号处理软件包提供的专用函数来直接求取FIR滤波器系数。在MATEAB中，提供了设计滤波器的函数。采用窗函数方法的函数firl，调用格式为：b=firl(n，ωn、window)或b=firl(n，ωn)，其中n是滤波器阶数，ωn是0～1的数，ωn=ωc／2π=0．25，window为窗函数类型。由于滤波器长度N为34，因此阶数n=N-1=33，则求取滤波系数的表达式为b=firl(33，0．25)。表1为利用MATLAB计算所得的滤波系数表。

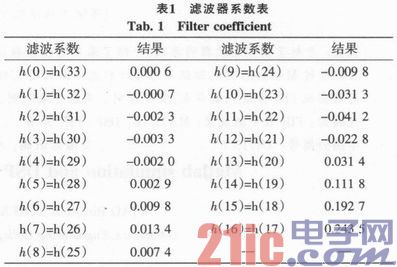
3．2 FIR数字滤波器MATLAB仿真设计

在满足各技术指标的前提下，经MATLAB仿真，图1为频率响应曲线，阻带衰减小于50 dB。图2为S=S1+S2+S3的波形，其中S1=sin(50x 2xπxt)，S2=0．15xsin(25x50x2xπxt)，S3=0．1xsin(20x50x2xπxt)。图3为滤除掉25次谐波S2和20次谐波S3后的波形图。

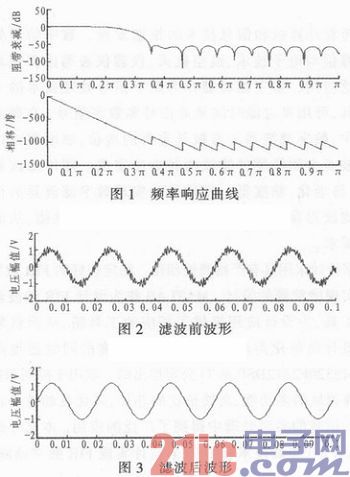
由滤波前后两个波形对比可以看出，该滤波器对20次以上谐波的滤除效果比较理想。

3．3 FIR数字滤波器的DSP实现

实现FIR滤波的核心器件是美国德州仪器公司生产的TMS320F2812DSP芯片。芯片内12位精度的A／D转换单元对输入的模拟信号进行采样，DSP读取采样值后对每一点进行FIR滤波处理，将数据存入内部存储器，为下一步进行FFT运算做准备。以下为FIR滤波器流程图。

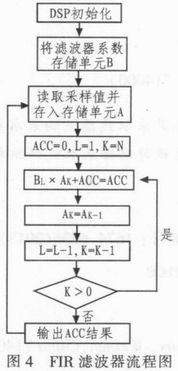
下面对程序流程作详细说明：

首先初始化DSP寄存器，分配存储单元，并定义一些变量名称，接着在数据存储区中开辟一个N单元的缓冲区，存放由MATLAB设计出的N个滤波系数。接下来读入采样值，并存入相应存储器A，然后开始滤波运算。具体运算步骤如下：

1)累加器ACC清零，初始化两个准备相乘的存储单元A与B的计数值K和L；

2)将第K个采样值AK与滤波器系数序列第L个数BL相乘(K+L=N+1)，并将乘积送入累加器进行累加；

3)将第K-1个采样值AK-1存入AK单元，此时AK中的原数值被覆盖；

4)重复(2)～(3)直至共完成N次乘加运算；

5)输出处理结果。

滤波运算采用FFT算法。DSP控制器特有的反序间接寻址，为FFT算法的实现提供了方便。间接寻址方式还可以实现增／减l或增／减一个变址量，这就很容易实现各种查表方法。

4 结束语

介绍了采用窗函数设计法用Matlab仿真技术和DSP技术来实现FIR滤波器的设计过程。Matlab仿真非常方便设计出具有严格线性相位要求的滤波器，在应用中只需对程序中滤波器的起始频率、截止频率、采样频率和窗函数等参数进行修改就可实现需要的滤波功能，实用性强。采用DSP控制器来实现FFT运算从而使设计实现实时控制。利用Matlab辅助DSP实现FIR滤波器的设计是解决滤波器从设计到实现的有效办法，这个方法可以大大缩短DSP应用程序的开发时间，提高了设计效率，具有很强的实用性。