摘要为改进滤波效果,提高去噪质量。通过分析软硬阈值去噪的原理和方法,为小波阚值信号处理提出了一种改进的去噪方法。该方法综合了软硬阈值的特点,对其参数进行优化设计,通过调节参数值以更好地获得阈值估计。针对改进后的去噪算法,通过Matlab仿真比较了传统的小波软硬阈值算法与该算法的消噪效果,结果表明,提出的方法有更好的消噪效果和稳定性。
关键词小波阈值去噪;阈值函数;信噪比;均方误差
小波变换与傅里叶变换、窗口傅里叶变换相比,它是一个时间和频率的局部变换,因而能有效地从信号中提取信息,通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析,解决了傅里叶变换不能解决的许多问题。
小波变换被誉为“数学显微镜”,是调和分析发展史上里程碑式的进展。小波理论被认为是对傅里叶分析的重大突破,是近年来信号处理领域的研究热点,许多学者将小波在理论上的研究成果应用到诸如图像压缩、特征提取、信号滤波和数据融合等方面。小波之所以在信号处理领域具有很大的优势,在于小波变换可以获得信号的多分辨率描述,同时,小波变换具有丰富的小波基可适应不同特征的信号。随着小波理论的发展,Mallat提出了模极大值重构滤波,Xu提出了空域相关滤波和Donoho提出了小波域阈值滤波来消除噪声。一般地,不同性质的噪声需要采用不同的消噪方法处理。
上述算法都存在参数的选取问题,不同的参数选取对滤波的效果会有一些差异。Donoho的传统小波阈值去噪方法的实现最简单、计算量最小。但其在理论上找到的最优通用阈值,实际应用中效果并不理想。因此,文中在Donoho的传统小波阈值去噪方法的基础上,改变了小波阈值函数的部分参数得到了一种新的小波阈值函数,既避免了硬阈值函数的不连续性,又可以自适应去噪,从而有效地保存了信号的边缘信息。仿真结果表明,改进后方法有更好的去噪性能。
1 小波阈值的去噪原理
小波变换具有一种“集中”的能力。信号经小波变换后,可以认为由信号产生的小波系数包括有信号的重要信息,其幅值较大,但数目较小,而噪声对应的小波系数幅值小。通过在不同尺度上选取一合适的阈值,并将小于该阈值的小波系数置零,而保留大于阈值的小波系数,从而使信号中的噪声得到有效的抑制,最后进行小波逆变换,得到滤波后的重构信号。
小波去噪的基本思路如图1所示。信号先经过预处理,然后利用小波变换讲信号分解到多尺度上,再对每一层小波系数进行阈值处理,最后对处理后的小波系数进行信号重构。
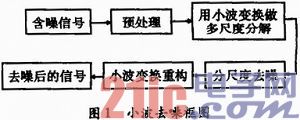
设一个含噪声的一维信号模型可以表示为f(i)=s(i)+n(i),其中s(i)为原始信号,n(i)为方差σ2的高斯白噪声,服从N(0,σ2)。
1.1 小波硬阈值去噪的步骤
(1)对信号求小波变换。
(2)除了最粗尺度信号外,将各细节信号作阈值处理,阈值t取为 ,当某位置小波变换值大于阈值时,保留原值,否则置零,用公式表示为
,当某位置小波变换值大于阈值时,保留原值,否则置零,用公式表示为

(3)利用小波变换重构,求出信号的滤波值。
1.2 小波软阈值去噪的步骤
(1)对信号求小波变换。
(2)除了最粗尺度信号外,将各细节信号作阈值处理,阈值t取为 ,当某位置小波变换大于阈值时,向着减小系数幅值的方向作一个收缩t,否则置零,用公式表示为
,当某位置小波变换大于阈值时,向着减小系数幅值的方向作一个收缩t,否则置零,用公式表示为
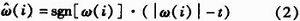
其中,sgn(x)为符号函数。
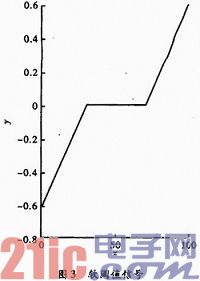
(3)进行小波变换重构,求出信号的滤波值。小波系数估计的软、硬阈值处理方法。如图2和图3所示。

2 小波阈值函数的改进
硬阈值函数构造虽然简单,但其在整个小波域内是不连续的,因此重构产生的信号会产生振荡,当噪声水平较高时,这种现象尤为明显,容易出现Pseudo-Gibbs现象。这与实际应用中经常要对阈值函数进行求导运算存在矛盾,具有一定的局限性;并在信号的边缘会产生许多人为的噪声点。在实际情况下,大于阈值的小波系数中也存在噪声信号的干扰,但硬阈值函数只对小于阈值的小波系数进行处理,对大于阈值的小波系数不加处理,这与事实不相符。
软阈值函数虽然在小波域内整体连续性好,但是由于当小波系数较大时,处理过的系数与原系数之间总存在恒定的偏差,这将直接影响重构信号与真实信悟的逼近程度,造成一定的高频信息损失,使信号的边缘变得模糊,给重构信号带来不可避免的误差。
在实际应用中,利用软阈值消噪信号比较光滑,但有着较大的信号失真。而利用硬阈值消噪对时变信号消噪效果是有限的。为克服软、硬阈值的缺点,文中将软阈值和硬阈值结合起来,在之前研究的基础上增加并优化了小波阈值函数的参数,构造了一类新的阈值函数为

其中α和β为调节因子,α,β在0和1之间选择不同的值可以改变滤波的效果。当a=0,β=0时式(3)等效于硬阈值函数,当α=1,β=1时上式等效于软阈值函数。当α,β取0~1之间的数时,随着|ω(i)|的增大, 不断变化,从而
不断变化,从而 不断变化,
不断变化, 和ω(i)的偏差绝对值逐渐减小为αt,这样可以有效避免软阈值方法中绝对值大的小波系数总存在恒定衰减的不足,用
和ω(i)的偏差绝对值逐渐减小为αt,这样可以有效避免软阈值方法中绝对值大的小波系数总存在恒定衰减的不足,用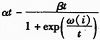 来衡量对其的衰减程度,动态减小了小波系数的衰减,从而避免了高频信息的损失,提高了信号去噪后的信噪比,增加了重构精度,改善了去噪的效果。
来衡量对其的衰减程度,动态减小了小波系数的衰减,从而避免了高频信息的损失,提高了信号去噪后的信噪比,增加了重构精度,改善了去噪的效果。
经验证α=0.4时,滤波的效果比较好。现在,关键在于β取何值合适。通过大量的仿真实验,当β=0.618时能获得更好的去噪效果,且处理起来比较方便。
3 仿真结果与评价
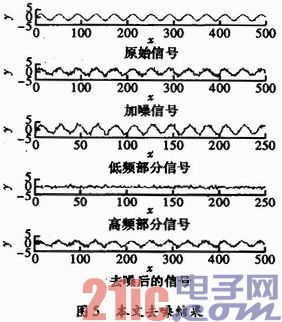
(1)为检验新阈值函数的去噪效果,利用matlab软件对一段信噪比为4,并含有高斯白噪声的信号,分别用软、硬阈值方法和文中提出的改进方法进行仿真实验。方法中的α,β分别取最优值α=0.4,β=0.618。选用的小波函数为db3,分解层数为3,并在每分解层数上按照Sqtwo log规则进行阈值的估计。去噪结果如图4和图5所示。

(2)信号去噪效果可以用信噪比(SNR)和均方误差(MSE)来描述。定义同一语音信号消噪处理后,均方误差(MSE)越小,信噪比(SNR)越大,则消噪效果越好,定义形式为

其中,s(i)是原始信号; 是由小波阈值处理后的信号。
是由小波阈值处理后的信号。
根据以上仿真和分析,3种方法对含噪声信号去噪后,信号的信噪比SNR和均方误差MSE如表1所示。

从表中的数据对比可以看出,文中提出的方法比软、硬阈值方法在信噪比SNR和均方误差MSE这两个性能指标上均有明显提高。
4 结束语
小波滤波已经应用于许多理论和应用领域,尤其在信号处理中发挥着越来越重要的作用,小渡去噪技术已成为信号处理研究的热点。文中介绍了小波阈值变换的原理以及软、硬阈值变换的原理和步骤,分析了软硬阈值变换的缺点,并且基于软、硬阈值方法对去噪能力的不同特点,提出了一种新的阈值函数,用该方法可以获得比软、硬阈值消噪更好的去噪效果和更高的信噪比,新的阈值函数可以避免高频信息的损失和软阈值方法中对绝对值大的小波系数总存在恒定衰减的不足,并且新的阈值可以提高消噪后信号的信噪比,减少信号的失真和震荡。