1 前言

随着物流、食品和石化等行业的不断发展，码垛机器人发挥着越来越重要的作用，它不仅可以准确、高效地完成码垛作业，而且可以降低工人的劳动强度，提高生产效率。

目前，国外主要机器人厂家，如ABB、FANUC等，均有较为完善的码垛机器人产品系列，垄断了国内外市场；而国内，码垛机器人的研究起步不久，还未有成熟的，产业化的码垛机器人产品出现。本文研究了ER300码垛机器人结构特点及运动空间，展现了一般码垛机器人与六自由度机器人的结构差异和运动空间形成方式。

2 码垛机器人机构分析

基于码垛任务的实际需要，码垛机器人通常具有四自由度。与一般垂直型六自由度串联工业机器人的结构不同，码垛机器人通过在肩部串联两个平行四边形结构使得腕关节旋转轴始终与地面垂直，从而使被抓持物始终处于水平状态；腕部结构简单，没有复杂的姿态调整结构。目前，码垛机器人使用较为广泛的结构之一，如图1所示：

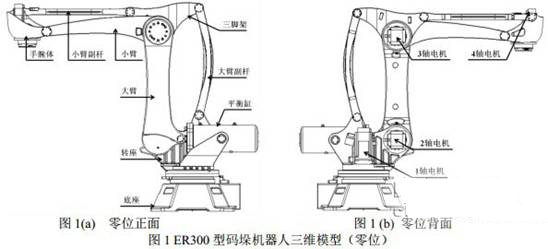
将图1中三维模型进一步简化为杆件连接（略去了1轴和平衡缸），如图2所示，A点为机器人2轴，B点为复合铰链，通过三角架分别与大臂和大臂副杆，与小臂和小臂副杆组成串联的平行四边形结构，使得运动过程中手腕体回转轴始终与地面保持垂直，从而手腕体中心D点相对小臂末端C点位置也保持不变。

此外，ER300机器人采用了将3轴电机和减速器均固定在三角架上的安装方式。该种连接方式使得三角架和大臂副杆承受了小臂、手腕体和负载等组件关于3轴的转矩M,但小臂不与大臂耦合旋转，在很大程度上简化机器人的运动方式和控制方法。

鉴于ER300码垛机器人没有复杂的耦合运动，本文不采用传统的D-H方法进行计算。为研究计算D点运动可达空间，这里将全局坐标系原点O0固定在1轴与地面的交点处，Y0与1轴重合，其余局部坐标系如图2所示

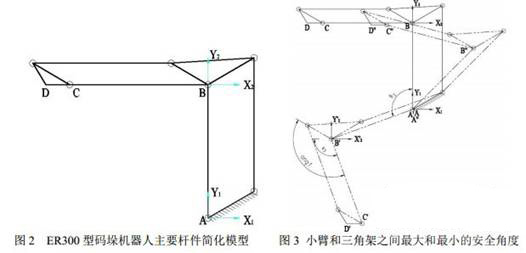
在全局坐标系中，各关节点坐标与关节旋转角之间的换算关系如下：

其中，R、H分别为1轴回转半径和底座高度；L2、L3分别为大臂和小臂长度；、分别为大臂相对Y1轴旋转角度，小臂相对X2轴旋转角度，本文规定逆时针旋转为正向；S为长。

零位时，2轴和3轴的旋转范围分别，.为保护码垛机器人末端平行四边形结构，防止杆件间发生干涉，ER300为小臂与三角架之间设定的安全角度为（如图3所示）。因此，小臂旋转角范围与大臂旋转角函数关系为：

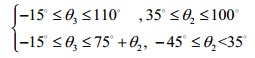
图3展现了在2轴两个极限位置时，小臂与三角架之间的最大和最小的安全角度。

3 ADAMS运动模拟

ADAMS是对机械系统的运动学与动力学进行仿真计算的经典软件。为进一步展示码垛机器人的运动空间形式，本文将solidworks建立的码垛机器人三维模型导入ADAMS,对机器人进行了运动模拟，其最大运动空间剖面轨迹如图4所示，该轨迹线反应了一般码垛机器人的最大运动空间结构。

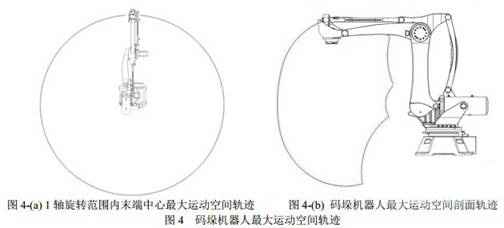
在完成上述图4-（b）的模拟中，2轴和3轴Motion驱动角速度如图5所示：

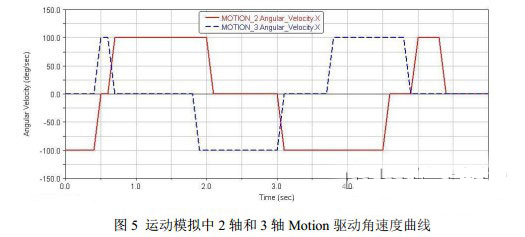
结合图4和图5可进一步看出，ER300机器人特定的结构使其在运动过程中，大小臂之间没有复杂的耦合运动，简化了机器人运动方式及控制方法。

仿真结果也显示，在机器人运动过程中，大臂副杆在某些位置承受了较大的拉力。由理论分析可知，当转矩M不变，大臂副杆的拉力F与其关于3轴的力臂L成反比例函数，从而在某些特定位置，力臂L的较小变化会导致F大幅变化。因此，在机器人设计过程中要充分保证大臂副杆及其组件的强度与刚度，以保证机器人的可靠性和准确性。

4 运动空间数值计算

为准确计算并验证码垛机器人的运动可达空间，本文采用了ER300码垛机器人的基本参数：R=400mm,H=835.5mm,L2=1250mm,L3=1300mm,W=225mm.利用matlab编程计算并绘制了码垛机器人手腕体D点的理论运动可达空间剖面，如图6所示：

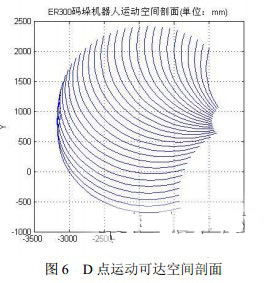
计算结果显示，当时，机器人末端中心D点达最大工作空间最高点；当时，机器人末端中心D点达最大工作空间最低点；当时，机器人达最大臂展位置，这三点位置决定了码垛机器人本体分别在垂直和水平方向上的最大码垛范围，是衡量码垛机器人工作性能的重要参数。

再与ADAMS模拟的运动轨迹点坐标计算结果对比，并分别考虑ADAMS模拟的轨迹求解精度误差和离散计算方法的误差因素，模拟结果和理论计算结果基本和设计目标一致，均能够达到最大臂展为3175mm,Y方向搬运高度3104mm的要求。

分别与ABB的IRB660-180、KUKA的KR180-2PA和KAWASAKI的ZD130S工作空间对比，结果显示在ER300的基本参数下，运动空间与上述同类机器人基本重合，能够达到市场的一般需求（臂展、码垛高度等）。

5 结论

本文通过对ER300码垛机器人机构的分析，展现了一般码垛机器人的杆件关系、运动形式；说明了该种机构优点的同时，也点出了其在设计过程中需要注意的问题；分别模拟和计算了码垛机器人的最大运动空间，验证了机器人的运动形式。

本文对码垛机器人的机构和运动分析，为该类机器人的研发提供了一定的理论依据和现实参照。