摘要:针对太阳光跟踪伺服系统中传统PID控制过程中的一些问题,通过对自适应模糊PID控制系统的分析,设计了一种双轴跟踪伺服系统自适应模糊PID控制器,同时在Simulink环境中建立了方位角跟踪传动机构仿真模型并完成了仿真。仿真结果表明,太阳光跟踪伺服系统自适应模糊PID控制器较传统PID控制器具有较强的稳定性、适应性与鲁棒性,在太阳光跟踪伺服系统控制领域具有重要的实用价值与应用空间。
关键词:自适应;模糊PID控制器;太阳光;跟踪伺服系统;Simulink仿真
0 引言
太阳能以其不竭性和环保优势已成为当今国内外最具有发展前景的新能源之一。高效采集太阳能是太阳能光伏发电的关键技术之一,本文以其广泛利用的基于步进电机的双轴跟踪伺服系统为研究对象,在传统PID控制器的基础上,结合模糊控制理论,设计一种自适应模糊PID控制器,并在Simulink环境中建立了方位角跟踪传动机构仿真模型并完成了仿真。
1 自适应模糊PID控制策略分析
在工业生产过程中,由于操作者经验不易精确描述,传统PID方法受到局限。运用模糊数学的基本理论和方法,把规则的条件、操作用模糊集表示,从而运用模糊推理即可自动实现对PID参数的最佳调整,并以此实现自适应模糊PID控制。
PID控制器能够在保证基本不影响系统稳定精度的前提下提高系统的相对稳定性,从而很好地改善系统的动态性能。其基本控制规律可描述为:
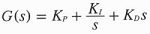
模糊控制实质上是一种非线性控制。模糊控制系统的鲁棒性强,干扰和参数变化对控制效果的影响被大大减弱,尤其适合于非线性、时变及纯滞后系统的控制。
结合PID与模糊控制两种算法的特征与优势,自适应模糊PID典型控制系统主要包括参数可调PID和模糊控制系统两部分,其中PID控制部分实现对系统的控制,自适应模糊控制部分以误差e和误差变化率作输入。它根据不同时刻的输入,利用模糊控制规则在线对PID参数KP、KI和KD进行修改,以满足控制器参数的不同要求,使被控对象具有良好的动态与静态性能,从而提高对被控对象的控制效果。
2 被控对象模型
目前,关于太阳能的伺服系统模型大多是对直流电机建模,并没有考虑到系统参数对跟踪系统的影响。本文采用的被控对象为基于步进电机的双轴跟踪伺服系统,其基本功能是使光伏阵列快速、平稳且准确地跟踪定位太阳光源。利用天文知识可以精确地获得太阳高度角和方位角。太阳光源跟踪伺服系统时刻检测光伏阵列和太阳光源的位置并将其输入到驱动运算单元,同时产生输出信号驱动两部电机,分别在水平面和铅垂面内运动,使太阳光时刻垂直入射到光伏阵列的表面上,从而达到准确和快速跟踪太阳光源的目的。图1所示是太阳能光源跟踪伺服系统的结构框图。
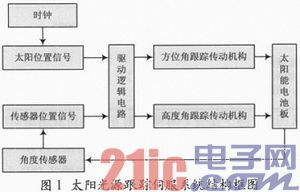
由于高度角跟踪传动机构与方位角传动机构工作时互不影响,下面以方位角跟踪传动机构为例进行建模和仿真研究。由文献可知,方位角跟踪传动机构的传递函数为:
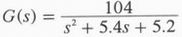
3 自适应模糊PID控制器的设计
本控制系统设计的关键是要先找出三个参数与误差e和误差变化率之间的模糊关系,要求在系统运行中不断检测e和误差变化率,根据模糊控制原理对三个参数进行在线修正以满足不同情况下对参数的不同要求,最终获得良好的动态和静态控制性能。
3.1 确定模糊控制器的结构
基于对系统的上述分析,模糊控制器采用两输入、三输出的控制器,将误差e和误差的变化率作为输入,将PID控制器的三个参数的修正值作为输出。其KP,KI,KD参数调整的算式如下:
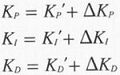
式中,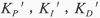 分别是参数前值;△KP,△KI,△KD分别为参数修正值。
分别是参数前值;△KP,△KI,△KD分别为参数修正值。
3.2 确定语言变量和语言值的隶属度函数
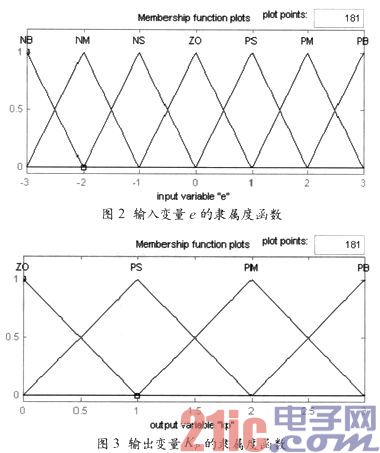
设定输入误差e的语言变量为E,误差变化率的语言变量为EC,两者的论域都为{-3,-2,-1,0,1,2,3},相应的语言值为{负大(NB),负中(NM),负小(NS),零(ZO),正小(PS),正中(PM),正大(PB)};输出KP的语言变量为△KP,KI的语言变量为△KI,KD的语言变量为△KD,三者的论域都为{0,1,2,3},相应的语言值为{零(ZO),正小(PS),正中(PM),正大(PB)}。输入输出变量的隶属度函数采用三角函数。图2所示是输入变量e的隶属度函数,输出变量KP的隶属度函数如图3所示。
3.3 建立模糊控制规则
PID参数的适应必须考虑到在不同时刻三个参数的作用以及相互之间的互联关系。对于不同的误差e和误差变化率,控制器参数的自整定原则可归纳如下:
(1)当误差较大时,为使系统具有较好的快速跟踪性能,应取较大的KP和较小的KD参数;同时为避免系统响应出现较大的超调,应对积分作用加以限制,并取较小的KI。
(2)当误差处于中等大小时,为使系统响应具有较小的超调,KP应取小一些;同时为保证系统的响应速度,KI和KD的大小要适中。
(3)当误差较小时,为保证系统具有较好的稳态特性,KP和KI应取得大一些。同时为避免系统在设定值附近出现振荡,并考虑系统的抗干扰性能,当误差变化率较小时,KD可取大些;当误差变化率较大时,KD应取小一些。
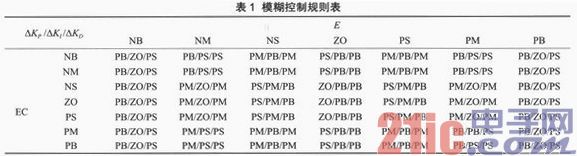
按以上原理并根据PID参数自适应原则和操作经验所列出的输出变量模糊控制规则如表1所列。
3.4 模糊量的清晰化
所谓模糊量的清晰化,就是把模糊推理后得到的模糊集转化为控制的数字值。这里采用重心法对模糊量进行清晰化。重心法是取隶属度函数曲线与横坐标围成面积的重心作为模糊推理的最终输出值,即:
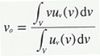
4 仿真结果分析
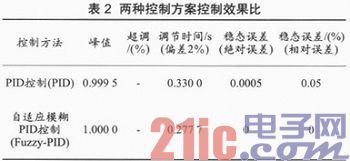
本文在Simulink环境中搭建了PID控制仿真模型和自适应模糊PID控制仿真模型。其中,KP,KI,KD保持文献中所提供的参数:KP=1.81 KI=0.4,KD=0.158。对仿真模型施加单位阶跃输入信号,仿真时间为5 s。其响应曲线如图4所示,误差变化曲线如图5所示,表2所列是其控制效果。
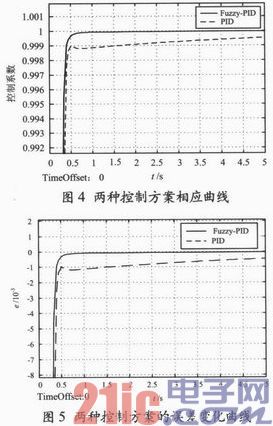
从图4、图5及表2两种控制方法的仿真结果对比来看,这种自适应模糊PID控制响应的速度较传统的PID要快。在稳态误差方面,自适应模糊PID控制较传统的PID小。综上所述,本太阳能伺服系统中的自适应模糊PID控制器具有响应时间短、稳态误差小等特点,而且系统也具有更好的适应性和鲁棒性。
5 结语
本文采用自适应模糊PID控制器对文献中提出的双轴跟踪伺服系统模型进行控制。通过在Simulink环境中的仿真结果发现,自适应模糊PID控制器较文献中传统的PID控制器具有较强的稳定性、适应性与鲁棒性,因而在双轴跟踪伺服系统的控制过程中具有重要的实用价值与应用空间。