引言

航空电子设备在生产、运输和使用过程中不可避免地要受到振动和冲击的作用。这些振动和冲击的作用可能导致电子设备的多种形式的失效，甚至破坏。这些振动和冲击引起的电子设备的破坏螺钉与螺母松脱、机箱的变形、PCB 焊点断裂剥离、器件引脚断裂等。尤其是随着PCB 不断向高精度、高密度、小间距、多层化、高速传输方向发展和大规模集成电路（VLSI）的飞速发展，它的功能更全、体积更小，封装引脚更多、更密的IC 和SOIC 不断涌现，特别是表面贴装技术（SMT）的广泛应用，都对PCB 组件提出了更高的挑战。

对航空电子设备而言，振动和冲击引起的故障会大大降低其可靠性，产生极其严重的后果。有关文献显示，航空电子产品因振动、冲击动力学环境所引起的失效率占总失效率的28.7%。在对航电设备进行的振动环境试验中，PCB 也时常有发生。通过对PCB 组件进行动力学分析、设计可以有效地降低其在环境试验中出现故障概率，提高航电产品的可靠性和质量。

动力学分析是以动态特性分析为基础的。通过对PCB 组件进行动态特性分析可以建立其动力学模型。只有建立起准确地动力学模型才可以对起进行有效地动力学分析。为此，本文试图采用有限元分析（FEA）与实验模态分析（EMA）相结合的预试验分析技术来进行某航电设备PCB 组件（图1 所示）的动态特性分析，并建立了该PCB 组件的有限元动力学分析模型。

1 有限元模态分析

作为一种成熟的数值分析技术，有限元分析技术（FEA）被广泛应用于电子设备PCB 组件的动态特性分析。并且，FEA 可以帮助工程师设计更可靠的PCB 组件，通过设计之初预测潜在的失效和疲劳。本文以某航空电子设备的PCB 组件（图1）为研究对象，其外形尺寸（长×宽×厚）为133.5mm×79mm×1.8mm，通过PCB 四个角处螺钉固定在电子设备的机壳上。该PCB 组件的外形尺寸和固定方式均与规定的标准试验PCB 相似，只是厚度大了一些。元器件和接插件采用表面贴装技术（SMT）与PCB 组装，其中元器件的封装主要为BGA、QFP 和SOP。

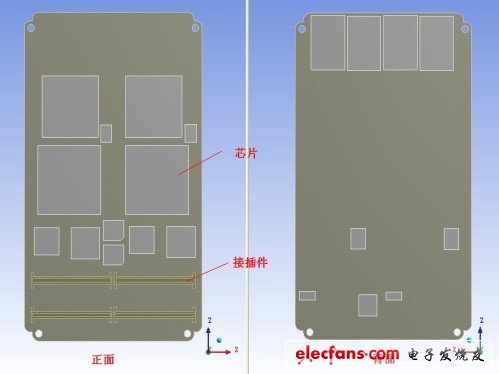
图1 对象PCB 组件

1.1 有限元分析模型

组成对象PCB 组件的各个部分的材料物理性能参数如表1 所示。根据该PCB 组件几何尺寸信息和相关材料信息，在ANSYS 中建立了有限元分析模型（图2）。由于要得到的是PCB组件整体所表现出的动态性能数据，而不是元器件本身的细节数据，因此建立模型时，对元器件和接插件进行了简化。具体地，采用矩形和正方形块来模拟元器件，接插件采用其大致外形来模拟。有限元分析模型中各部位均采用三维实体单元（SOLID187）来进行网格划分（采用实体单元进行网格划分，虽然一定程度上增大了计算量，但是从CAD 到CAE 的模型的工作量大大减少，有利于工程应用推广），并且元器件与PCB、接插件与PCB 之间的连接均采用多点约束（MPC）来模拟。同时，由于电子机壳的刚度远大于PCB 组件的刚度，在有限元模型中在四个角处的螺钉孔处施加固定支撑约束来模拟该PCB 组件与设备机壳的螺钉连接。

表1 对象PCB 各组成部分材料的物性参数

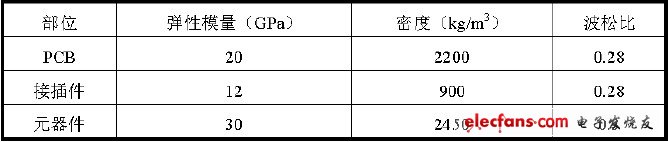
图2 对象PCB 组件的有限元模型

1.2 有限元模态分析结果

建立起对象PCB 组件的有限元模型，并采用兰索斯分块法（Block Lanczos Method）进行模态分析。模态分析就是通过求解系统的特征方程，一般多自由度系统的特征方程可以成式（1）所示的形式，来得到系统的特征值和特征向量，亦即振动系统固有频率和振型。

式中，［M］－系统的质量矩阵，有限元模态分析中由单元质量矩阵组装而成；［K］－系统的刚度矩阵，有限元模态分析中由单元刚度矩阵组装而成；{X}—系统的位移向量；ω－系统的特征值。

通过模态分析，得到了采用四颗螺钉固定的对象PCB 组件的前三阶固有频率和振型，具体见表2。该PCB 组件的第1 阶振型为一阶弯曲，第2 阶振型为扭转，第3 阶振型为正弦波状弯曲。这些振型与得到的四颗螺钉固定下JEDEC 标准板相似。

表2 有限元模态分析结果

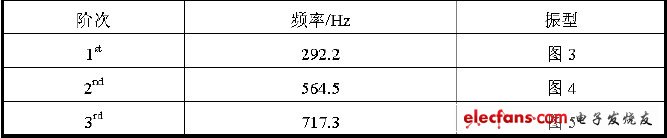
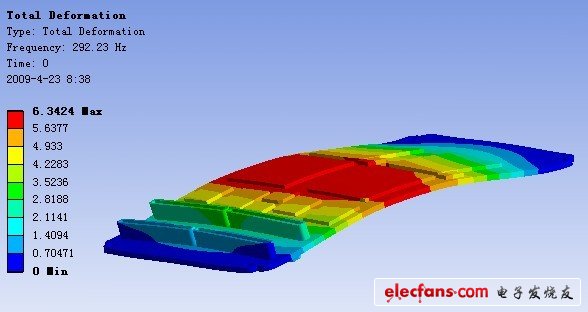
图3 PCB 组件第1 阶振型（FEA）

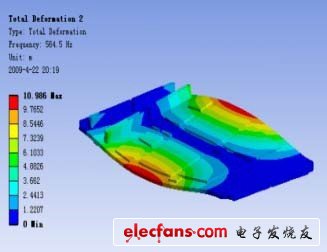
图4 PCB 组件第2 阶振型（FEA）

图5 PCB 组件第3 阶振型（FEA）

2 实验模态分析

实验模态分析是若干工程学科的综合，它通过建立试验“装置”、估计频响函数、系统识别、识别结果验证4 个步骤得到系统的模态参数：固有频率、振型、模态阻尼等。实验模态分析的结果经常被用来检验有限元分析模型的有效性和正确性。为了检验本文所建立的对象PCB 组件的有限元分析模型的有效性和模态分析结果的正确性，对该PCB 组件进行了实验模态分析。

2.1 实验模态分析系统

本文采用的模态试验系统由激振器、力传感器、夹具、试验对象、激光测振仪（IVS200）、动态信号分析仪（DP730）、数据采集记录软件（SignalCalc730）/模态分析软件（ME’Scope V4）及PC 构成，如图6 所示。

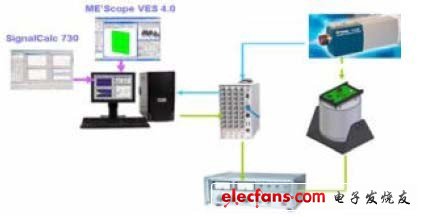
图6 试验模态分析系统的构成

为了使得实验模态分析中对象PCB 组件的边界条件与有限元模态分析中的边界条件一致，将对象PCB 组件通过4 个15mm 高的压铆螺母柱用螺钉固定在夹具板上。具体如图7 所示。实验过程采用正弦扫频激励试验对象，通过激光测振仪来采激PCB 组件的响应，有动态信号分析仪和数据处理软件来计算PCB 组件上各点的频率响应函数（FRF），最后利用模态分析软件从中辨识系统的模态参数。

图7 对象PCB 组件在夹具上的安装

2.2 实验模态分析结果

选取对象PCB 组件上距离相等的若干个点，通过逐点扫描的方式获得各点的频率响应函数（FRF），进而辨识出PCB 组件的模态参数。具体辨识结果列在表3 中。

表3 实验模态分析结果

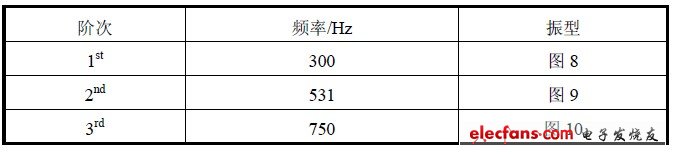
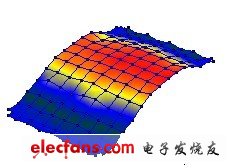
图8 PCB 组件第1 阶振型（EMA）

图9 PCB 组件第2 阶振型（EMA）

图10 PCB 组件第3 阶振型（EMA）

3 结果比较及讨论

为了检验有限元模态分析结果与实验模态分析结果的一致性，进而判断所建立的对象PCB 组件有限元模型的正确性和与实验模型的相关程度，需要将有限元模态分析结果与实验模态分析结果进行比较，具体见表4。有限元模态分析结果和实验模态分析结果的比较过程需要经历两个步骤：首先是比较二者的固有频率值，然后再对二者的模态的相关程度（MAC）进行比较。对固有频率的比较是最常用的步骤，但是如果实验模态分析的结果和有限元模态分析的结果不是按照严格按照阶次对应的话，仅对固有频率进行比较就会存在出现错误的风险。这是由于系统中的两个相同的频率值可能对应两个截然不同的振型。因此，只有同时进行以上两个步骤才能准确判断有限元分析模型与实验模型的相关程度。

表4 模态分析结果比较

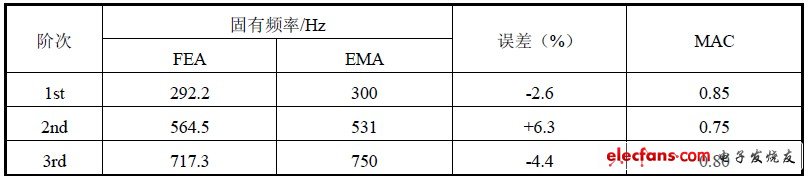
表4 显示有限元模态分析结果和实验模态分析结果具有很好的一致性。有限元模态分析得到固有频率与实验结果相比误差小于7%，二者的振型的相关程度大于0.75。并且，实验得到振型恰好与模态分析得到的振型是按阶次对应的。

4 总结

文中以航电的设备的PCB 组件为研究对象，首先建立了有限元分析模型，并采用兰索斯分块法计算了其前3 阶固有频率和振型。然后，为了检验该计算结果的正确性，并确定有限元模型与实际PCB 组件的相关程度，利用实验模态分析系统对对象PCB 组件进行了实验模态分析。最后，计算结果和实验结果比较显示：有限元模态分析结果和实验模态分析结果具有很好的一致性，文中得到的对象PCB 组件的动态特性数据是正确的、可靠的，该有限元模型可以用于后续的动力学响应分析工作。