本文作者maxfiner，毕业于西安电子科技大学，拥有信号与信息处理专业硕士学位。maxfiner曾供职于华为通信技 术公司无线通信部门，拥有多年的工程项目研发经验，同时兼备算法理论研究，仿真验证，以及对应的硬件设计实现能力；具备通信物理层开发设计各个方面的实战 经验...

从事信号处理相关工作，不可避免的用到一些数学知识。通常来说，用到啥，就回头去看啥，或者说，缺啥补啥。有一些数学知识，是频繁和反复用到的，因此有必要把它们汇总下。数学方面的东西，只看数学书籍的话，一般情况下，是相当乏味和枯燥的，但是和实际应用结合起来，就发现数学的魅力、力量和威力还是很强大的。和实际问题结合起来，数学也就变得有趣起来。在这里，暂时举出三例，后续继续丰富和完善。

一 复数的概念

复数可以说是我们从小到大一路走来，最后学到的一种数了。从历史的角度看，它也是最后引入的几个数之一，直到最近几百年才开始引入并推广应用。它是为了解方程的方便而引入的，而且一开始还一直不被人们接受，这些人中包括很多大数学家。可见一个新的事物，一个新的概念，一种新的思想，要想被人接受是很困难的，很漫长的一件事情。但是，随着时间的发展，由于它的独特价值，最终被人接受并广泛应用。复数除了解方程之外，在工程领域，最能体现复数应用价值的是两个方向，一个是量子力学，一个就是电磁学。

复数的概念在电子工程，电磁场与电磁波等领域应用极为广泛，在信号处理方向更是如此。不论是信号处理的基础理论——傅里叶变换，还是信号的基带表示和带通表示，解析表示，不论是频谱的分析，还是讨论信号的时移和相位，都离不开复数这个有力的工具的支撑。

相关概念：

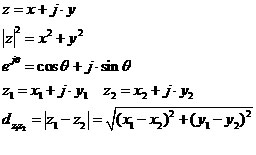
应用举例简述如下，在相关章节会分别进行更详细的介绍。

BPSK，QPSK，16QAM等调制方式，信号星座可看做信号正交分量和同相分量的复数域的表示。

发射机的EVM测试，即根据星座点在复平面上的位置进行计算，计算的目标就是实际测得的星座点和参考星座点之间的距离，或者说就是复平面上两个点的距离。

接收机存在某个频率偏移时，星座图上的星座点会以恒定速率旋转，围绕原点做匀速圆周运动，运动角速度和频率偏移大小成正比。

电路的阻抗分析、谐振分析均以复数运算为基础。

实信号的频谱是共轭对称的。频谱的镜像可用共轭成分来表示。

安捷伦和罗德施瓦茨都有矢量信号发生器，矢量信号分析仪，这些信号都是复数形式的信号。

信道估计算法，本质上可以看做是复数的除法运算。

发射机的正交上变频，接收机的正交下变频，本质上可以看做复数的乘法运算。

接收机频偏的补偿，本质上可以看做复数的乘法运算。

发射机链路和接收机链路上各个节点的功率的计算，为复数的模平方的计算，在信号功率监测，模拟自动增益控制（AAGC），数字自动增益控制（DAGC）等领域中有广泛应用。

二 信号的伸缩和平移

信号的伸缩和平移，尤其是平移，在信号处理的理论和实践中有着广泛的应用。信号时域的平移和频域的相移之间的关系，是非常奇妙而又应用广泛的一对关系。信号的伸缩和平移，从数学上来说，就是函数的伸缩和平移的应用，这是高中初等数学的范畴，应该是非常一般的，即使很久不用数学也不会忘记的一个概念和方法。但是因为它如此的重要，因此有必要单独拿出来进行一个小小的总结，从而更好的利用这一有效工具去解决各种信号处理相关的问题。这一章节专门讨论和总结平移。伸缩的讨论等到真正用到它时（比如信号的插值和抽取）再进行相应描述。

信号的平移，最简单的是记住四个字——“加左减右”。即移动量是正值，则整个信号波形向左移动，即向x坐标轴的负轴方向移动。移动量是负值，则整个信号波形向右移动，即向x坐标轴的正轴方向移动。虽然想象左右比想象上下的心理反应时间要慢些，但多多体会就会熟记于心的。

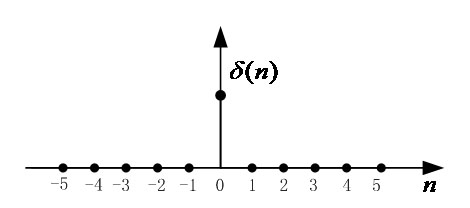
举个例子，比如单位采样信号为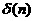不妨想一下，和单位冲击信号有何区别呢？），如下图所示：

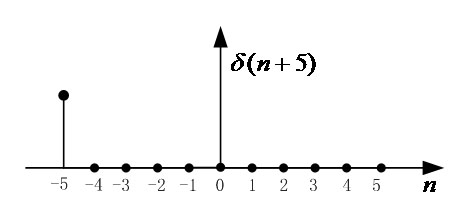
若是信号形式为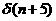则整个波形向左移动5个采样点，如下图所示：

对于一般的一个信号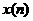可以根据单位采样信号的平移性质，表示成如下形式：

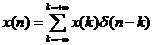
也就是说，任何一个离散信号，都可以表示成单位采样信号的线性叠加形式。从信号与系统的角度来说，这是系统线性叠加的体现。这里的系统，当然是线性时不变系统，满足齐次性，叠加性和时不变性，这是我们所有关于信号与系统的分析的前提。

三 和差化积公式

积化和差公式最普遍、最频繁的应用就是信号的上下变频处理。后续我们结合信号的基带表示和带通表示的时候会进行更细致的描述。

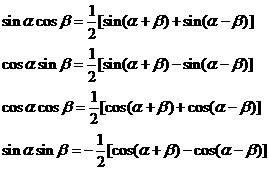
若是一下子记不住这四个公式，可以先理解第三个，然后依次类推。虽然说数学需要理解，但是实践证明，为了更好和更高效的应用，一些极其常用的概念和公式还是记牢的好。

比如诸如积化和差之类的三角公式，比如香农公式，比如2的N次方（2<N<16）。

下期开讲——精通信号处理设计小Tips（6）：卷积是怎么得到的？敬请关注！