数字滤波器分为有限冲激响应(FIR)和无限冲激响应(IIR)两种。其中，FIR数字滤波器在实现任意幅频特性的同时能够保证严格的线性相位特性。由于其单位冲激响应是有限的，没有输出到输入的反馈，因此系统是稳定系统。FIR数字滤波器在通信、图像处理、模式识别等领域有着广泛应用。

在实时性要求较高的应用场合，相比于DSP芯片或专用芯片，采用可编程芯片FPGA实现FIR数字滤波器具有高速、高精度、高灵活性的优点。数字滤波器的设计方法有多种，常用的有窗函数法、频率抽样法和最佳一致逼近法，但这些设计方法在设计滤波器尤其是高阶滤波器时工作量较大。而利用Matlab信号处理工具箱进行数字滤波器的设计，能够减少工作量，提高设计效率。文中首先使用Matlab设计滤波器系数，然后利用FPGA实现系统。

在FPGA中，进行传统乘法运算占用大量的硬件资源，分布式算法利用ROM查找表将固定系数的乘累加运算转换成查表操作，避免了乘法运算，查表后的数据执行的都是简单的加法运算，可以较大程度地提高运算速度。分布式算法分为全串行分布式算法和全并行分布式算法，全串行分布式算法资源消耗少但运算速度慢，全并行分布式算法资源消耗少但运算速度快。兼顾运算速度与资源消耗，本文采用改进并行分布式算法进行FIR数字滤波器设计。

1 FIR数字滤波器基本理论

对于FIR数字滤波器系统，其冲激响应是有限长的，系统函数可记为

式中，x(n)是采样输入序列;h(i)是滤波器系数;N是滤波器抽头数;y(n)是滤波器输出序列。

2 分布式算法

分布式算法(Distributed Arithmetic，DA)是一项重要的FPGA技术，广泛地应用在卷积、相关、DFF计算和RNS反演映射等乘积和中。有关DA算法的讨论可以追溯到1973年Croisier发表的论文，而DA算法的推广工作则由Peled和Liu完成。虽然DA算法较早被提出，但是一直到可编程门阵列的查找表结构出现，这种算法才重新受到重视，成为一种重要的FIR数字滤波器设计方法。

DA算法是一种以实现乘加运算为目的的运算方法，其与传统实现乘加运算算法的不同之处在于执行部分积运算的先后顺序不同。DA算法在完成乘加功能时是通过将各输入数据每一位产生的部分积预先进行相加形成相应部分积，然后再对相应部分积进行加权累加形成最终结果;而传统算法是等到所有乘积产生之后再进行相加来完成乘加运算。与传统算法相比，DA算法可以大幅减少硬件电路规模，易实现流水线处理，提高了电路的执行速度。DA算法原理如下。

对于有符号系统，采用补码实现，输入序列x(n)表示为

式中，y(n)是输出序列;x(n)是输入序列;h(i)是滤波器系数;B是x(n)二进制补码的位数;xb(n)是x(n)的第6位，N是滤波器抽头数。

本文采用改进并行DA算法进行FIR数字滤波器设计，通过引入倍频模块减少LUT的个数来节省资源消耗，同时保证运算速度。该算法仅使用一个LUT并结合流水线寄存器的使用来提高系统运算速度。算法原理是让输入数据每一个相同位同时寻址，将寻址内容进行相应的移位累加操作得到最终输出，算法如图1所示。

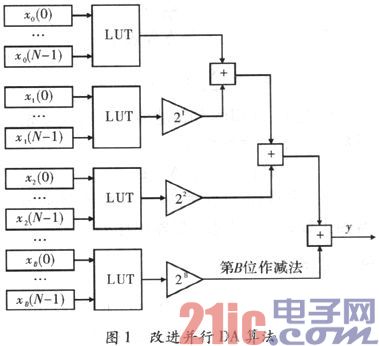
3 滤波器系数设计与量化

文中滤波器系数通过Matlab工具箱中的FDATool进行设计，滤波器设计指标如下。滤波器类型：低通;设计方法：FIR Kaiser窗，Beta= 0.5;阶数：15阶;采样频率：10 MHz;截止频率：1.5 MHz;输入数据宽度：12位;滤波器系数宽度：12位。

由于FPGA只能进行定点数运算，需要将浮点滤波器系数量化为定点数。将h(n)扩大210倍，然后表示为12位二进制补码。滤波器系数与量化补码如表1所示。

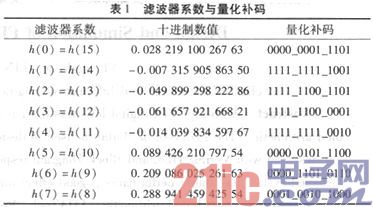
4 FPGA实现

用FPGA设计FIR数字滤波器时，利用滤波器系数的对称性，将16抽头设计转化为8抽头设计。首先将输入数据存入移位寄存器中，通过延时进行预相加，然后以预相加结果数据的相同位的值为地址进行查表操作。根据分布式算法公式，依次进行移位累加操作，但对数据最高位进行移位相减操作才能得到正确的滤波输出。整个系统由时钟控制模块，数据输入模块，查找表模块，移位累加模块以及截位模块组成。

4.1 时钟控制模块

采用的FPGA芯片是Altera公司的CycloneII系列EP2C5T144C6，其时钟晶振是50 MHz。为提高系统运算速度，由于输入数据是12位，数据输入模块一次输出8位地址，因此需要设计一个采样信号12倍频模块，即得到120 MHz信号。时钟控制模块主要包括采样信号12倍频模块和采样信号模块。其中，采样信号倍频模块利用QuartusII中PLL实现，采样信号模块利用倍频模块通过硬件描述语言Verilog HDL编程分频实现。

4.2 数据输入模块

该模块的功能是将输入数据转化为8位查找表的地址，包括移位寄存、预相加和并串转换。首先将数据存入移位寄存器中，通过延时进行预相加，最后对预相加结果进行并串转换。

4.3 查找表模块

查找表模块可以利用QuartusII中的lpm_rom实现，但需要手工计算每个地址对应的数据输出，由于输入8位地址数据，使用lpm_rom实现查找表的计算量过大，所以该模块通过硬件描述语言Verilog HDL编程实现。模块还可继续拆分为4输入或2输入查找表。

4.4 移位累加模块

系统核心模块，主要对查找表模块输出数据进行移位累加操作，由于输入12位数据，因此要进行12次移位操作，前11次移位进行加法操作，第12次移位进行减法操作。为使累加结果不溢出，要进行冗余设计。

若输入数据与滤波器系数均为B位，对于有符号系统，移位累加器长度M=2B+log2N-1，其中N为滤波器抽头数。该移位累加模块输出数据宽度为27位。

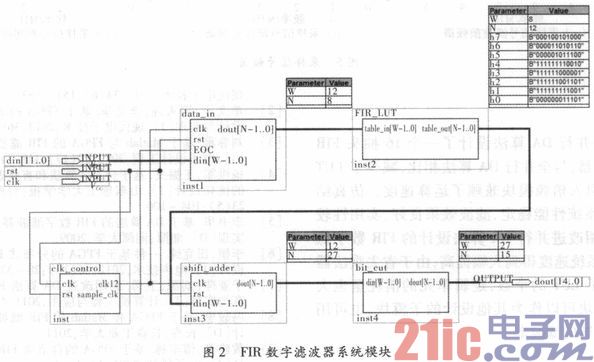
4.5 截位模块

移位累加模块输出27位数据，由于其对应的10进制数值较大，不便于分析，因此对移位累加模块的输出数据进行截位。截位模块的功能是通过移位截取27位输入数据的高15位。

5 Matlab与QuartusII联合仿真

FIR数字滤波器输入与输出均是数字信号，通过Matlab编程模拟A/D转换得到滤波器输入数据，然后将输入数据送到滤波器输入端口并进行仿真得到输出波形，最后再通过Matlab编程模拟D/A转换将输出数字信号以模拟信号波形形式展现。具体步骤如下：首先利用Matlab编写得到*.mif文件的M程序，输入0.5 MHz和2.5 MHz正弦相加信号，幅度均为15。然后用QuartusII中lpm_rom模块得到滤波器输入数据，再用QuartusII对系统模块进行仿真，将仿真波形*.vwf文件另存为*.tbl文件，系统模块仿真波形如图3所示，最后用Matlab读取该文件中的数据，得到采样信号时域波形与频谱。

6 结束语

采用改进并行DA算法设计了一个16抽头FIR数字低通滤波器，与全并行DA算法相比，减少了LUT的个数，同时引入倍频模块兼顾了运算速度。仿真结果表明，设计系统性能稳定、滤波效果良好、实用性较强。同时，利用改进并行DA算法设计的FIR数字低通滤波器，其系统速度得到大幅提高，由于省去乘法器的使用，减少了LUT的个数，逻辑单元的消耗量也大幅降低。该模块可以作为其他设计的子模块，也可用于设计更高阶数的滤波器。