摘要:本文提出了一种由传统的钳位二极管三电平逆变器和一个辅助电路组成的新型拓扑结构,目的是保证其直流母线侧两个电容电压相等。同时,在控制算法上利用该新型拓扑结构提出数学模型,提出了一种非线性鲁棒控制策略的控制器,并成功应用于APF中。
本文实现方法是由数学模型推导出状态空间模型,分析整理后得到三个单输入单输出(SISO)鲁棒控制器,分别用来负载电流的谐波补偿,控制直流母线电压和保证直流侧两个电容电压平衡,该设计的三个SISO 控制器保证非线性补偿之间的相互独立性,互不干扰。整个设计思路在matlab2010b/simulink 平台上仿真,结果表明,采用该非线性鲁棒控制算法,电网的谐波电流可以很好补偿;在负载变化下,主电路的直流母线电压保持在其参考值和电容电压保持相等,电网电流的补偿动态性能效果也非常明显。
1.引言
随着电力电子技术的发展,谐波治理已成为当前的热点问题,很多学者进行了研究。而应用最为广泛的是APF,即有源电力滤波器。在APF 的主电路中,三电平逆变器电路与传统两电平相优势有很多,首先是低纹波电流,每个功率器件仅承受1/(n-1)的母线电压(n 为电平数);其次是电平数的增加,改善了输出电压波形,减小了输出电压波形畸变(THD);还可以以较低的开关频率获得和高开关频率下两电平变换器相同的输出电压波形,无需输出变压器,大大地减小了系统的体积和损耗,另外,研究直流侧电压平衡问题也一直是热点。
本论文提出了主电路为三电平有源滤波器,针对直流侧的两电容电压不不平衡,提出了一个改进了主电路的拓扑结构,进而根据该拓扑分析其数学模型,运用鲁棒控制方法分离出三个单独的非线性控制器,同时利用李亚普洛夫判断稳定性的条件,最后在matlab 仿真平台上验证思路的可行性。
2.三电平电路模型分析
如下图 1 所示,是一个比较典型的二极管箝位的三电平为主电路的SAPF(Shunt Active Power Filter)拓扑图。谐波无功电流检测电路将负载电流iL 谐波电流和无功电流分离开,然后把它们反相并产生出补偿电流ic 的调制波信号ic*,通过驱动隔离电路时三电平逆变器产生补偿电流ic,从而抵消电网中的谐波成分,实现谐波的补偿,这就是谐波补偿的基本原理。
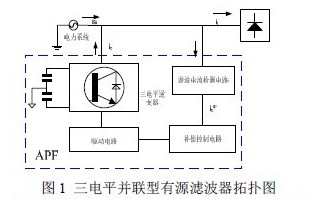
在设计APF 装置中,主电路设计非常关键,常见的三电平电路由如图2 所示当中的主电路模块(蓝色框图),至于直流侧电压往往采用一些PI 的算法实现,从而保证直流侧的两个电容电压保持平衡,但是算法效果一般。为此,提出了改进的电路拓扑图。
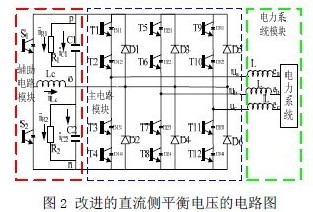
如图2所示,改进的直流侧平衡电压的电路图由传统的三个桥臂的二极管钳位主电路和一个辅助电路组成。该辅助电路设计的是由类似T 型的一个电感和两个IGBT 电路,为方便记忆,定义该模型为“T 型辅助电路”(图2 中红色框图)。设计思路是假设通过电感Lc 的电压是低于直流侧uc1 电容电压,则当辅助电路中S1 的开关闭合,电流是从电容C1 流出,而电感流进,此时若S2 开关关闭,电流转移到UC2 的电容中;相反,假设通过电感Lc 的电压是低于直流侧uC2 电容电压,则当辅助电路中S2 的开关闭合,电流是从电容C2 流出,而电感流进,此时若S1 开关关闭,电流转移到UC1 的电容中。因此,通过适当的调节占空比这些补充的开关S1,S2,就可以保证直流侧电容上下两臂电压保持平衡。
分析图2,可根据基尔霍夫电压定理有主电路的数学模型如下:

上(2)(3)式中,id,iq,ed,eq,ud,uq 分别对应abc坐标系下的ik,ek,uk(k=a,b,c)的转换在dq坐标系下的值,w 对应于三相电力系统的频率rad/s.
下面分析辅助电路,为了更好描述把不妨辅助电路进行等效。显然在电容两侧的电压设定为uc1,uc2,对应地电流分别为ic1,ic2,另外考虑到开关损耗,故在电容两侧各并联一个电阻,分别为R1,R2,如图2 所示的辅助模块,对应的电流为iR1,iR2,开关S1,S2,且要求互补,不妨假定为S1=0 表示上臂断开,S1=1 表示上臂开关闭合。因此,不难得到下面的式子。
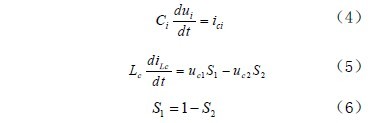
上式(4)中i=1、2 分别对应于电容两侧电压,且C1=C2=C,公式(5)对应于电感两侧的电压与电容两侧电压之间的关系,公式(6)表示两个开关状态关系。
等效后的辅助电路与主电路之间平的有功功率相等[5],于是又得到下面的公式(7)(8)。
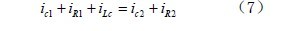

上面式子中用C 取代了C1 和C2,即C1=C2=C,Δudc=uc1-uc2,udc=uc1+uc2,注意到由abc 转换到dq 坐标系下eq 分量因为与对应的iq 电流是相垂直的,故在(11)式中没有出现eq 这个分量,即无功功率为0.下面将对上面所描述式子进行详细分析,并用推导出对应的鲁棒控制器的表达式。
上面式子中用C 取代了C1 和C2,即C1=C2=C,Δudc=uc1-uc2,udc=uc1+uc2,注意到由abc 转换到dq 坐标系下eq 分量因为与对应的iq 电流是相垂直的,故在(11)式中没有出现eq 这个分量,即无功功率为0.下面将对上面所描述式子进行详细分析,并用推导出对应的鲁棒控制器的表达式。
3.非线性鲁棒控制器的设计
3.1 d 轴电流控制器的设计
为了确保id 跟踪id*,设计了d 轴电流控制器,同时在udc 也保证与udc*保持一致,实现的表达式是根据(2)和(11)两个式子,该子系统只有一个输入ud,控制器的框图如下图3 所示。不妨令:
k1=3ed/C,k2=ed/Lc, k3=(icR1+icR2-iLC+2iLCS1)/C于是可以根据上式子把(2)(11)两个式子变为如下状态方程:
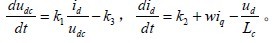
注意到上式子中k1,k2,k3 未知,即假定该参数值是未知的,但必须标称值是已知的,对应于u1,u2,u3.给定值与实际值之间的误差变量定义为:Δudc=udc*-udc ,Δid=id*-id .
同时为了保证Δudc 保持为0,设计一个udc 控制器:
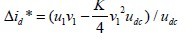

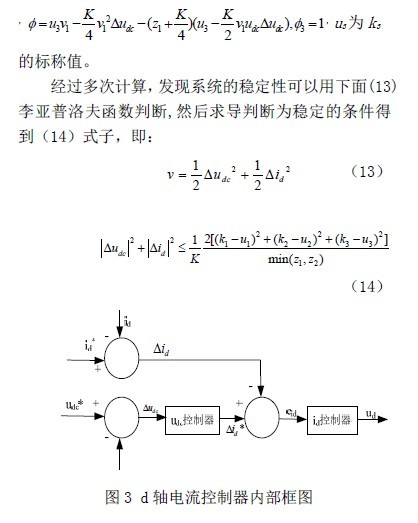
上式(14)证明了该设计的闭环系统是最终有界的,其中K 值要合理的进行选择,仿真发现该值不能太小。
3.2 q 轴电流控制器的设计
该控制器是用于iq 完全跟踪参考电流iq* ,该子系统所代表的方程是(3)式, 用于合成该控制器方程,该系统输入量为uq,输出量为iq,扰动量为eq/L-wid.在这里,一个逆推设计方法是用来寻找控制器的结构和其方程,设计如图4 所示。

上面(15)式子中k4假设不知道,但是标称值知道为u4,同时它们之间误差要使之为0,因此iq控制器简化的等式为:

3.3 直流侧电容平衡控制器的设计
考虑子系统中(9)和(10)来设计平衡电路控制器。注意到这子系统有两个外部干扰:直流母线 udc电压和有功功率在转换器的损失电流。该控制器是用来调节Δudc 到零,从而达到补偿的外部干扰。 控制输入为S1,S2=1-S1.控制器的结构和其使用反推得到递归方程方法,这种控制设计技术是利用多个控制器,基本思路是首先当前值给定值iL*与实际iL 值匹配并保持直流Δudc 为零。其次,控制输入S1 是计算驱动电流实际的iL 跟踪给定iL*值,控制输入S2 方法类似不再累赘。图5 中给出了内部结构的电容电压均衡器,下一步介绍如何控制器方程获得。为清晰起见,定义下面的参数和变量:k5=(iR1-iR2)/C 和eΔudc=Δudc*-Δudc=Δudc*,即Δudc=0.为此(9)式子可以变形为:
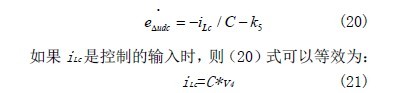
其中V4=k5*Δudc-u5+KΔudc/4,k5*Δudc 是系统的稳定条件,KΔudc/4 为系统k5 与u5 之间的补充误差值,k5,K 为正增益。如果iLc 不为控制系统的输入时,可以定义一个误差量ΔiLc=iLc*-iLc,新的变化动态子系统有如下的表达式:


4. 仿真分析
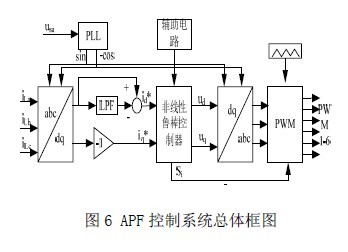
仿真在 matlab2010b/simulink 平台上验证,这里把整个系统搭建如6 所示,需说明的是非线性鲁棒控制器设计的就是控制三个输出量ud,uq,Si,用锁相环提供与电源电源相同相位,由低通滤波器(LPF)得到id的参考电流id*,iq 直接经过一个值为-1 放大器,得到参考电流iq*.仿真具体参数是:输入的电压源a 相是幅值设置为220sqrt(2),频率为50Hz,其他b,c 相只是改变一下相位,相差120°,输出滤波电感三相均设置为3.5e-3H,负载的电阻为10Ω,电感为3H.逆变器直流侧的两个电容取1100uF,udc*取800V,正增益K 设置为8,采用变步长方式ode23tb,总仿真时间为0.1s.仿真结果得到补偿后得到图7 所示的波形,补偿效果很好。当负载发生突变时,仿真设计在0.05s 处突加负载,这是电网的电流如图8 所示,经过补偿后得到如图9 所示,同时直流侧电压在负载突变的情况下很快也恢复到原来电压,如图10 所示的直流侧电压Uc1,Uc2 及它们之和的波形图。因此,整个仿真结果得出该控制器的可行性。


5 结论
本论文中提出了采用辅助电路来保证整个直流母线电容器的电压平衡,来设计有源电力滤波器,进而提出了相关的数学模型,分析后得三个单输入单输出的非线性鲁棒控制器的数学表达式,并通过李亚普洛夫判断稳定性,得到稳定的条件。每个控制器分别对应不同的作用,且系统的子模块之间的是相互独立。经过仿真结果表明了该辅助电路及鲁棒非线性控制器用来平衡电容电压,补偿谐波电流是非常有效的。为具体实现该有源滤波器的装置提供了有力的依据。