在当今的混合信号系统世界里，许多应用都需要测量和处理大量的模拟信号，包括但不限于电压、电流、温度、压力、加速度、pH值、流量和ECG等。相关应用领域包括可控环境下的实验室和医疗设备，也包括运行在恶劣工作条件下的工业设备。需要测量的模拟信号范围很大，包括ECG系统中的几微伏电压到发电站的数千伏电压等。

无论是什么应用、环境或待测量的信号量，基本的信号采集系统都包含一个放大和调节信号的模拟前端以及将模拟信号转换为数字值、然后由微处理器加以处理的模数转换器 (ADC)。模拟前端可能是一个简单的放大器，也可能是包含多级放大器和滤波器的复杂系统。

基本信号调节电路的方框图如下所示：

放大器增益

假定系统是理想状态，那么ADC输出由以下方程式表示：

这里，VIN为输入电压

A为放大器增益

VFS为ADC的范围

N为ADC的分辨率

对于ADC计数而言，微处理器根据以下方程式计算输入电压：

可惜的是，在现实世界中，没有所谓“理想”的情况，系统必须应对引入系统并影响ADC输出的误差。最重要的误差也就是我们本文将要讨论的误差——偏移误差和增益误差。

偏移误差

图2显示了范围介于+2.5V之间的8位ADC示意图。X轴表示输入电压，Y轴表示ADC计数。蓝线为理想的ADC输出。红线则为实际的ADC输出。请注意，实际输出与理想状态不同，这种差异就叫作偏移误差。

所有运算放大器的输入都存在有限的偏移电压。偏移电压被添加到输入信号上，然后被放大器增益放大并在输出处表现出来。除了放大器级之外，ADC还有自己的偏移电压，也会增加到系统误差上。偏移误差是附加误差，能轻松地从系统中移除。

增益误差

图3显示了同样范围介于+2.5V之间的8位ADC示意图。请注意，实际输出斜率与理想输出的斜率不同，这种差异就叫作增益误差。

增益误差主要是由于放大器中增益设定电阻的容差和ADC中参考电压的容差而造成的。增益误差是一种缩放型误差，也能轻松地从系统中移除。

代表实际系统的数学方程式

理想的采集系统可以借助简单的数学方程式表达，如方程式3：

这里，y是系统输出或ADC计数

mi是系统的理想增益

x是输入电压

在方程式中引入偏移误差和增益误差，则有：

这里，ma是实际系统中带有误差的增益

C是偏移误差

图4显示了存在偏移误差和增益误差的系统：

片上系统 (SoC) 是在单颗芯片上集成模拟和数字外设以及微处理器的混合信号控制器，其不仅在同一器件中集成了模拟前端所需的所有组件，如放大器、滤波器、ADC等，而且还可提供灵活的路由选项。利用这些灵活的资源，我们能精确地解决偏移误差和增益误差问题。

下面让我们讨论一些用来消除偏移和增益误差广泛采用的校准方法。每种方法都有自己的优点和缺点。根据应用不同，我们可使用一种方法、或者多种方法的组合，从而实现最高的精度。

两点校准

这种校准方法能同时解决偏移误差和增益误差。在方程式4中，如果实际增益ma和偏移C为已知，那么实际输入可用方程式5进行计算：

参数ma和C均可通过两点校准过程加以确定：

1、在模拟前端输入处施加0V电压，测量ADC输出，并记录为Offset (C)。

2、在输入处施加已知参考电压并测量ADC输出。为了实现最佳性能，参考电压应大于满量程值的90%。

3. 计算计数/电压 (ma) 或电压/计数 (1/ma) 增益。

4、将偏移和增益值存储在非易失性存储器中，并在实际测量中使用该值。

当偏移和增益值被存储之后，我们就能使用以下方法测量输入信号：

1. 测量输入ADC计数。

2. 使用偏移和增益值计算输入电压。

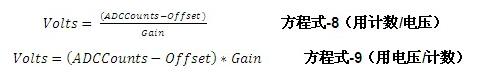
根据应用不同，用于执行偏移或刻度校准的触发器可用开关实现，或者也可通过通信接口接受命令实现。

刻度可以是被测量的实际单位的函数。举例来说，如果您测量分流器上压降的电流，那么您不必测量电压再得出电流，而是可以直接对分流器施加参考电流并通过计数/安培来计算刻度。这就消除了分流电阻容差所造成的误差问题。

缺点：

使用这种偏移和增益补偿方法有两个缺点：

1. 运算放大器的偏移有自身的温度系数，会随温度而变化。这会导致在进行校准温度以外的其它温度上会出现偏移误差。

2. 两点校准会在制造进程中多加一个步骤。