摘要随着现代电子战中电磁环境的日益复杂，军用接收机需具备同时处理多个信道信号的能力，即具备全概率截获能力。信道化接收机可将一个复杂信号分成多个信道，从而方便后续处理。文中利用一种简化的结构验证了该种信道化方案的可行性，并节省了逻辑资源。

关键词 数字下变频;多相滤波;信道化

在电子战中，传统上主要采用扫频式搜索接收机，但其截获概率受搜索速度的影响较为严重，且因其受到搜索速度与分辨率之间关系的制约，所以扫频式接收机对跳频信号的截获效果很不理想。信道化接收机是对某个频段的信号全概率接收的接收机，而基于多相结构的信道化接收机相对于传统意义上的信道化接收机对同一频段信号而言所需硬件资源更少，且更易于实现。其相对传统的信道化接收机凭借其高效的多相结构，使其在多信道处理方面得到了广泛应用，是接收机的发展趋势。

1 多相滤波结构的信道化原理

1.1 信道的划分

因实信号频谱具有对称特性，所以其频带划分较为特殊，这里只对[0，π]上的频谱进行信道划分。若划分K个信道，各信道的中心频率为ωk=kπ/K+π/2K，其中，k=0，1，…，K-1。

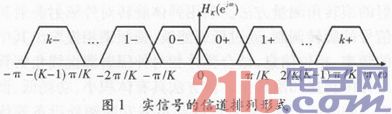
由傅里叶变换可知，低通滤波器的频谱包括正负对称的两部分。为使信道的划分如图1所示，需将滤波函数的频谱全部移到正半轴，这里对滤波器的频谱函数做如下变换

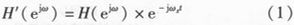
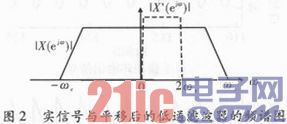
此时反映到频域如图2所示，因此，采用复FIR滤波器对输入的实信号进行滤波。

1.2 基于多相结构滤波器的信道化原理

信道化的主要过程为，先将每个信道乘以

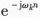
，对信号做频域的搬移，再经过低通滤波器，滤除高频分量，并将频率均降到基带，做下变频，最终进行抽取。信道化结构如图3所示。

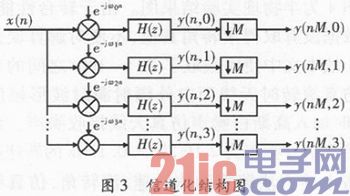
图中，ωk表示第k信道的中心频率，H(z)表示低通滤波器。但问题在于，每个信道的信号做完一系列计算之后，再作抽取，中间会有较多数据的计算损耗。因此，需要一种简化的方法使计算变得更加高效。

根据图3可知

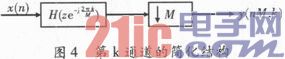
此时只剩低通滤波和抽取两部分，可用Noble等效再次化简，为此先对FIR滤波器作如下变换

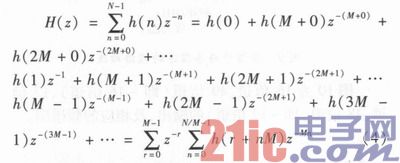
根据Noble等效，可将抽取移到FIR滤波之前，如图5所示。

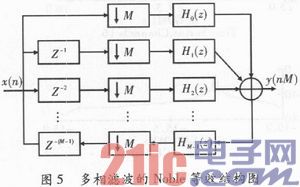
结合图5并纵观整个系统，容易发现x(n)可看成经过串并转换之后分别进入各个信道，即x(n)的第n=mM+k周期的数据进入第k信道做运算。

此时已经完成多相滤波的结构简化，回到本文的信道化方案中，根据式(3)和图4，将z用

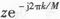
代替，则式(4)可作如下变换

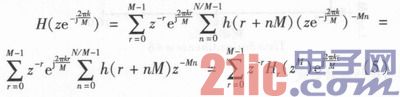
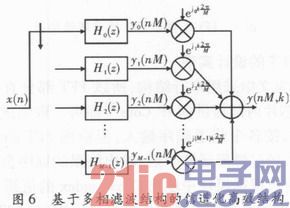
则有最终的信道化高效结构如图6所示，令每个信道FIR滤波器的输出为yr(nM)，则总输出为

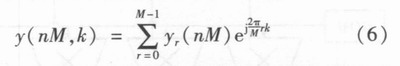
从式(6)可看出，这是一个离散傅里叶变换的形式。因此，整个信道化的过程由FIR滤波和FFT两部分组成。这大幅降低了运算量并节省了资源。

2 硬件实现

文中采用Xilinx系列芯片。假设输入信号为0～32 MHz的实信号，由奈圭斯特采样定理可知，FPGA的工作频率定为64 MHz。0～32 MHz实信号的频域在[-32 MHz，32 MHz]之间，若使每个信道的带宽为1 MHz则需划分64个信道。而做后续处理时，只计算[0，π]区间的32个信道输出的信号即可。

由于工作频率较低，而信道划分较多，所以整个过程需采用串行方式处理。FPGA内部实现的总体框图如图7所示。

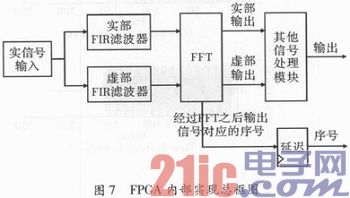
2.1 FIR滤波器的设计实现

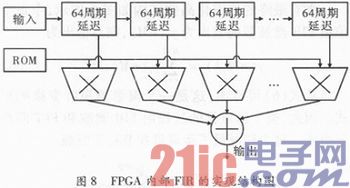
FPGA内部的FIR滤波器实现结构，如图8所示，512点的FIR滤波器，因共64个信道，所以每个信道要做8个乘法运算。每个信道FIR系数的确定及存储顺序参照式(4)，将参数存到ROM中，每个周期读取8个系数，与输入信号相乘，乘得的8个结果再做累加，则是每个信道经FIR计算的结果。因采用串行结构，故每个信道的计算结果会从输出端口，按信道序号的顺序，循环输出。

2.2 FFT的设计实现

因为文中采用串行结构，所以FFT部分直接采用Xilinx芯片内部提供的IP Core即可。数据进入FFT模块时，按各个信道顺序输入，但根据FFT的计算方法可知，经过蝶形运算后，输出结果的顺序会发生改变，此时可根据模块中输出口xK_index的值辨认某个周期输出的是第几信道的计算结果。因此在FPGA中做后续逻辑时，需注意计算结果与相应序号要保持对齐，以免计算错误。

3 Matlab仿真分析

利用Matlab进行仿真验证。采样频率为64MHz，带宽1MHz，若输入为实信号频率为15.7MHz，则信号与各信道的频谱曲线如图9所示。

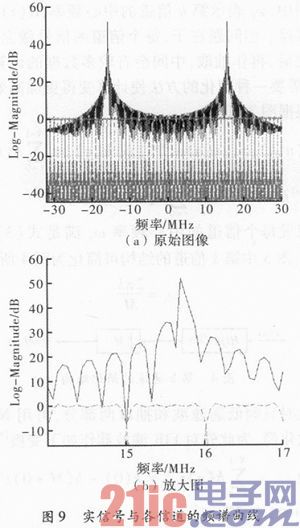
图10为16信道、49信道(即-16信道)、17信道、48信道(即-17信道)的输出，及相应的频谱图。

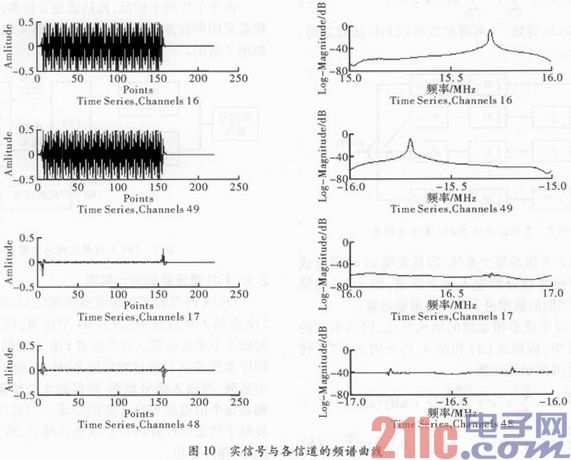
由图可见信号出现在第16信道内，信号频率均落到[0 MHz，1 MHz]之间，符合设计要求。

4 结束语

介绍了一种基于多相滤波结构的信道化方法，该方法结构简单、大幅节省了资源，并在FPGA上采用串行结构，完成了32信道的划分。这种多信道的划分和同时处理的能力，可较好地完成对目标信号的全概率截获，在电子侦查领域具有较高的应用价值。此外，文中介绍的系统工作频率较低，可采用串行结构节省资源。若信号和系统的工作频率较高，则可采用并行结构，此时若需要，也可利用语言实现FFT的并行处理结构，以提高处理速度。