摘要在雷达接收回波信号过程中，杂波信号的存在对有用信号的检测和提取会产生干扰。因此，必须抑制杂波。文中提出了一种基于最小功率准则的自适应MTI滤波器的设计，通过仿真波形看出，该方法可以有效地抑制动杂波。

现代雷达面临的任务日益复杂，这就要求提高雷达在复杂多变环境中的检测性能，然而在雷达工作的过程中，可能会碰到诸如地物、海浪、云雨及敌人施放的金属箔等杂波。杂波分为固定杂波和动杂波。对于固定杂波，需要采用凹口位于零频附近的滤波器来抑制。然而对于频谱位置有相应多普勒频移的动杂波，就需要滤波器的凹口对准杂波平均多普勒频率位置才能得到良好的抑制效果。

1 相关理论介绍

MTI技术是最早用于杂波抑制的技术之一。MTI的设计思路是使滤波器止带凹口尽量对准杂波谱的中心频率。典型的MTI系统通常采用非递归的有限冲击响应(FIR)滤波器来实现对杂波的抑制，设输入信号为x(t)，每级延迟线的延迟时间为Tr，则MTI滤波器的输出为

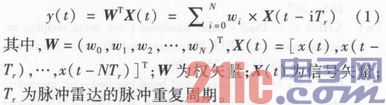
通常用一次对消和二次对消来作MTI处理，但这样的处理对静止杂波有较好的效果，但对动杂波的处理则不甚理想。随着自适应信号处理的发展，可用自适应技术来设计最佳滤波器。本文采用最小功率准则，自适应估计杂波的中心频率，使得滤波器的凹口对准杂波的中心频率从而达到抑制杂波的目的。

假定杂波比目标和噪声大得多，当滤波器加权系数为最佳时，杂波被大量滤出，输出主要为信号分量。但当权系数不是最佳时，由于杂波没有被大量滤出，而由于杂波强，则输出总功率较大。所以只要保证输出功率最小，就能使信号杂波比达到最大。

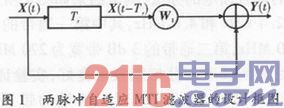
由图1可以看出

2 多普勒相位估计补偿的AMTI方法

基于以上杂波对消方法的缺点，文中介绍了一种基于最小功率多普勒相位系数补偿对消的AMTI方法。首先，采用自适应双门限进行杂波位置的判定，然后对所确定的杂波位置信号进行杂波多普勒相位估计，最后采用最小功率准则选择杂波多普勒相位补偿系数并进行杂波的自适应对消，实现框图如图2所示。

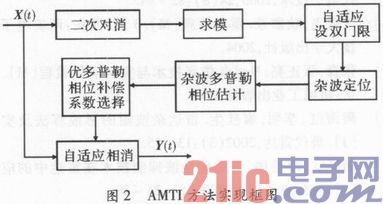
3 仿真结果

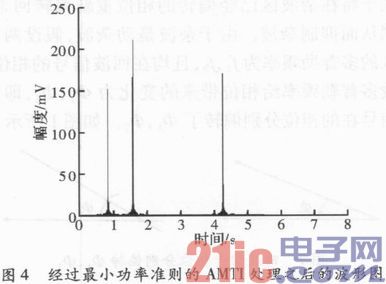
对上述理论进行仿真，雷达参数设置如下：发射信号波长0.1 m，脉冲重复频率1 kHz，脉冲宽度42μs，带宽2 MHz，杂波谱采用瑞利分布来描述，假设在雷达的探测范围中都有强杂波的影响，而在距离16 km，30 km和80.25 km有3个动目标，其多普勒频率分别为800 Hz，500 Hz和300 Hz。仿真结果如图3所示。

从图3中可以看出，目标完全淹没在强杂波中，如果仅用上述处理方法，很难检测出目标信号。

通过对图3和图4的对比，可以看出，最小功率准则的AMTI处理可以有效地抑制强杂波，较好地检测出了目标信号。

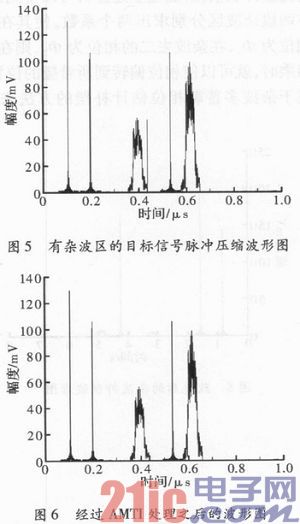
假设在雷达的探测范围里，分别在60 km和93 km处，有两段杂波区，其宽度分别为39μs和20μs，其多普勒频率分别为800 Hz和570 Hz，仿真结果如下所示。

通过图5和图6对比可知，在有两段杂波区杂波抑制过程中，基于最小功率准则的AMTI处理效果不明显，而在整个雷达探测范围里有强杂波的杂波抑制过程中，效果明显。

通过式(2)看出，通过前一回波与后一回波与系数W相乘相消来达到抑制杂波的目标的，系数W的作用相当于将在杂波区已经偏转的相位重新偏转回来，再相消从而抑制杂波。由于杂波是动杂波，假设两段杂波区的多普勒频率为f1，f2，且均在回波信号的相位上，假设多普勒频率给相位带来的变化为φ1，φ2，即在回波信号在的相位分别偏转了φ1，φ2。如图7所示。

然而如式(5)所示，用前一回波和后一回波所有的点来计算W，假设W的相位为φW，当后一回波与系数W相乘时，理想状况是在杂波区使回波的相位分别偏转φ1，φ2，这样才能在前一回波的相消过程中消去杂波，然而W的求解注定其相位φw不可能在两段杂波区分别为φ1和φ2，而只能为一个中间值，所以，得到了图6的仿真结果。

要完全抑制杂波，通过上述分析可以得到启示，如果能在两段杂波区分别求出两个系数，使其在杂波区一的相位为φ1，在杂波去二的相位为φ2，则在与后一回波相乘时，就可以使相位偏转到所希望的位置，且可通过基于杂波多普勒相位估计补偿的方法来求解系数W。

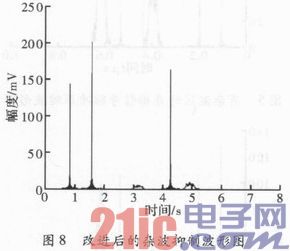
由图8可知，改进后的AMTI算法可以较好地抑制杂波，效果良好。

4 结束语

在雷达接收回波信号的过程中，杂波信号的存在对有用信号的检测和提取一直起着干扰的作用，所以必须抑制杂波，而动目标显示(MT I)技术对静止杂波有较好的抑制能力，但对动杂波则显得无能为力，采用自适应技术则可有效抑制动杂波。本文提出了一种抑制动杂波的方法，并且给出了相应的Matlab仿真波形，通过仿真波形可以看出，该方法可以有效地抑制杂波。