二维FIR滤波器的FPGA实现
时间:05-19 16:08 阅读:1651次
*温馨提示:点击图片可以放大观看高清大图
简介:对二维信号实时处理涉及大量的复数运算且对运算速度要求很高,因此二维有限长单位脉冲响应滤波器(2D—FIR)的结构比一维滤波器要复杂得多。通过对二维滤波器重要运算单元复数乘法的分析、优化减小了其所需实数乘法器的个数。采用Quartus II软件综合可以得到算法优化后的二维滤波器占用逻辑资源减少了16%,工作速度提高了13%。
摘要:对二维信号实时处理涉及大量的复数运算且对运算速度要求很高,因此二维有限长单位脉冲响应滤波器(2D—FIR)的结构比一维滤波器要复杂得多。通过对二维滤波器重要运算单元复数乘法的分析、优化减小了其所需实数乘法器的个数。采用Quartus II软件综合可以得到算法优化后的二维滤波器占用逻辑资源减少了16%,工作速度提高了13%。
关键词:现场可编程门阵列;二维有限长单位脉冲响应滤波器:复数乘法;信号处理
O 引言
二维有限长单位脉冲响应滤波器(2D—FIR)用于对二维信号的处理,如在通信领域中广泛采用2D-FIR完成对I、Q两支路基带信号的滤波[1]。由于涉及大量复数运算并且实时性要求高,如果不对算法作优化在技术上很难实现。目前主要设计方案是利用FPGA厂商提供的一维FIR知识产权核(IP),组成二维滤波器[2]。这种方案没有考滤复数运算的特点,不可能在算法上优化,而且IP核的内部代码是不可修改的,因此在不同厂商的器件上不可移植。2D_FIR的复数运算都需转成实数运算来实现的,而其中实数乘法运算占用逻辑资源远比实数加法多。通过分析复数乘法特点,减小其所需实数乘法器个数就可以减小逻辑资源占用率并提高运算速度。这种方案优点在于直接优化算法,不会受IP核限制可移植性很强。
1 2D—FlR的设计
采用FPGA设计复数FIR滤波器常见的方案[2]为:用FPGA厂商提供的4个实数FIR滤波器IP核组合成2D—FIR滤波器。很明显这种设计没有考虑复数运算的特点,2D—FIR滤波器占用资源至少4倍于实数FIR滤波器,硬件资源耗费过大,性能也会受到不小的影响。因此从算法上分析并优化滤波器的结构非常必要。
1.1 算法优化
2D—FIR滤波器结构采用卷积型,它对输入数据的处理就是进行卷积运算[3],如(1)式所示:

(1)式中各量全为复数:xρ(n)为输入数据 为滤波器抽头系数。由(1)式可以看出其运算过程是
为滤波器抽头系数。由(1)式可以看出其运算过程是 先作复数乘法运算,再将乘积结果作复数加法得到
先作复数乘法运算,再将乘积结果作复数加法得到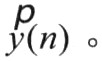 一个复数乘法由4个实数乘法和2个实数加法构成。而相同位数的实数乘法器与实数加法器相比会占更多的硬件资源,也会对电路性能产生更多的负面影响。通过优化后的复数乘法如下:
一个复数乘法由4个实数乘法和2个实数加法构成。而相同位数的实数乘法器与实数加法器相比会占更多的硬件资源,也会对电路性能产生更多的负面影响。通过优化后的复数乘法如下:
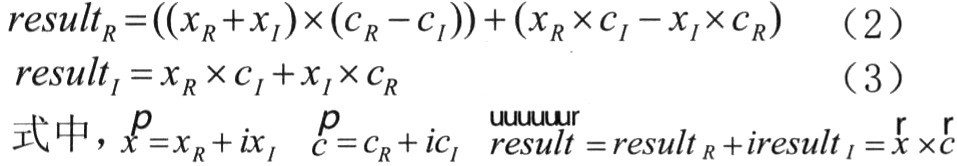
比较(2)式和(3)式可以得到两个式子中xR×CI、xI×CR是共有项,故优化后的复乘法器需3个实数乘法器和5个实数加法器。如果抽头系数为常数cR-cI,可以事先计算,还可以省一个加法器。通过Quartus II编译、分析可以看到复乘法器性能提升了近14%,同时器件资源占用却下降了17%。因为滤波器共需15个复乘法器所以总体上减小的逻辑单元非常可观。
1.2 FPGA实现
考虑到2D—FIR滤波器的运用背景,除HDTV信道中要求抽头数大于100以外抽头数定为15已能满足一般通信系统的要求,输入数据和抽头系统数据宽度都为16位。其中,输入数据整数位(含符号位)为4位,小数位为12位,抽头系数整数位为(含符号位)3位,小数位为13位,输出数据与输入数据位宽选取一样。FPGA实现浮点小数运算代价太大,解决小数运算的方法是将小数表示为带符号的整数[2],运算后再对结果进行截尾处理。
由于2D—FIR滤波器中有很多乘法和加法器,它们都是大型组合逻辑电路,所以需要在电路上进一步优化。引入多级流水线是提升电路工作速度很有效的方法[4],文献[2]所采用的转置卷积型滤波器结构实质是在乘法器之间加入了一级流水线,但相对于多级流水线其对电路性能提升并不大。本文加流水线具体的做法是用寄存器将组合电路分成若干延时相近的小型组合电路,同时将乘法和加法器分别设置为3级和2级流水线以满足流水线配平原则。FPGA选用Altera公司专用于数字信号处理的EPlS20芯片,经过Quartus II编译后从报告中看到滤波器工作频率为146MHz,占用芯片54%的逻辑资源。
2 仿真及结论
电路仿真结果如图1所示,输入数据为[1+3*i,5,0,0,0 0,0,2,3.5,1+2*i,0,0…],抽头系数在模块中设为[0.851*i,0,0,1,-i,1.15-0.4.i,0,0,0,i, 0, 0, 0, 0,图1 2D—FIR滤波器电路时序仿真结果
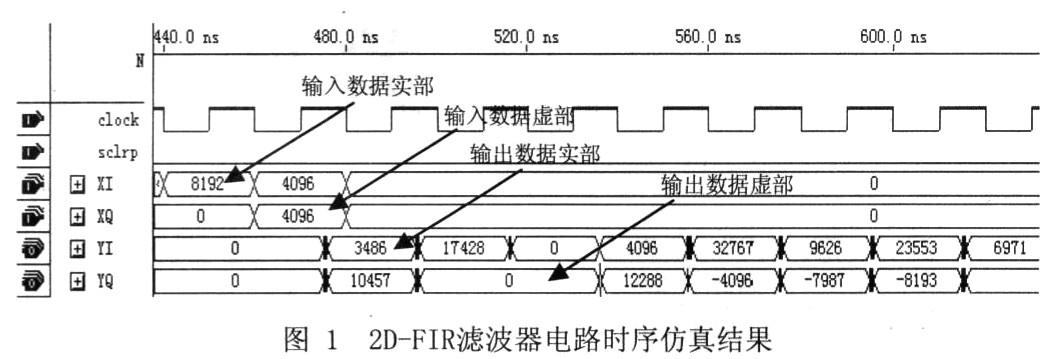
0.1*i]。为了方便验证仿真结果,事先计算出输出数据并转化为带符号位的整数[-10457+3486i,0+17428i,0,4096+12288i,32768—4096i,9626—7987i…]。从图3中的仿真结果可以看到,经过十几个时钟周期的延时后复数FIR滤波器的输出为[3486+10457 i,17428,0,4096+12288i,32767-4096i,9626-7987i…],前面两个数据与计算结果不一致是因为:复滤波器刚开始工作时内部移位寄存器默认的数据是0而不是外部输入的数据,当数据全部装载入滤波器后,计算结果完全满足设计要求。
通过对算法与电路的优化使2D—FIR滤波器的性能提高了13%,逻辑资源的占用减小了16%。文中所提出的方案比常规方法更有效,而且具有更强的可移植性。