1 引 言

癫痫的诊断主要依靠临床病史，脑电图检查可作为一种极有价值的辅助诊断手段。本文选用基于TI公司的TMS320C54X系列的DSP芯片开发平台。借助DSP快速数据处理的优点，对癫痫脑电信号进行小波变换，然后滤除小尺度(高频)成分，保留大尺寸(低频)成分，最后再对处理后的信号进行重建。实现流程如图1所示。

2 离散小波变换算法

离散小波变换的一个突破性成果是S.Mallat于1989年在多分辨分析的基础上提出的快速算法一一Mallat算法[2]。Mallat算法在小波分析中的作用相当于快速傅里叶变换(FFT)在傅里叶分析中的作用，他标志着小波分析走上了宽阔的应用领域。Mallat算法又称为塔式算法，他由小波滤波器H，G和h，g对信号进行分解和重构[3]。分解算法为：

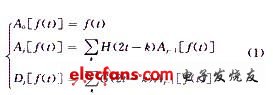
式中，t为离散时间序列号，t=1，2，…，N;f(t)为原始信号;j为层数或小波尺度，j=1，2，…，J，J=log2N;H，G

为时域中的小波分解滤波器，实际上是滤波器系数;Aj为信号f(t)在第j层的逼近部分(即低频成分)的小波系数;Dj为信号f(t)在第j层的细节部分(即高频部分)的小波系数。

式(1)的含义是：假定所检测的离散信号f(t)为A。信号，信号f(t)在第2j尺度(第j层)的近似部分，即低频部分的小波系数Aj是通过第2j-1尺度(第j-1层)的逼近部分的小波系数Aj-1与滤波器H卷积，然后将卷积的结果隔点采样得到的;而信号f(t)在第2j尺度(第j层)的细节部分，即高频部分的小波系数Dj是通过第2j-1尺度(第j-1层)的逼似部分的小波系数与分解滤波器G卷积，然后将卷积的结果隔点采样得到的。

通过式(1)的分解，在每一尺度2j上(或第j层上)信号f(t)被分解为近似部分的小波系数Aj(在低频子带上)和细节部分的小波系数D，(在高频子带上)。

重构算法为：

式中，j为分解的层数，若分解的最高层即分解的深度为J，则j=J-1，J-2，…，1，0;h，g为时域中的小波重构滤波器，实际上是滤波器系数。

式(2)的含义是：信号f(t)在第2j尺度(第j层)的近似部分的小波系数，即低频部分的小波系数Aj是通过第2j+1尺度(第j+1层)的逼近部分的小波系数Aj+1隔点插零后与重构滤波器h卷积以及第2j+1尺度(第j+1层)的细节部分的小波系数Dj+1隔点插零后与重构滤波器g卷积，然后求和得到的。不断重复这一过程，直到第2°尺度，得到重构信号。

3 小波变换的DSP实现

3.1 脑电信号在CCS 2.2上的输入与输出

CCS 2.2(Code Composer Studio)是由TI公司推出的一种针对标准TMS320调试接口的集成开发环境(IDE)，利用CCS集成开发环境，用户可以完成工程定义、程序编辑、编译链接、调试和数据分析等工作环节[4]。我们把十进制的浮点数用两个十六进制数进行表示，采用C语言实现。

再利用CCS中的File->Load Data将十六进制的数据导入到DSP的相应内存中去。

反过来，DSP处理之后的数据利用CCS的数据导出File->Save以文本文件形式保存，再用C语言进行数据逆转化，把两个十六进制数进行转化成十进制的浮点数。

其中的result数组就是十进制的浮点型，origin数组就是十六进制的浮点型。

3.2 核心汇编程序介绍

以下是以16位定点乘法实现32位浮点乘法的部分汇编程序：

3.3 实验结果与分析

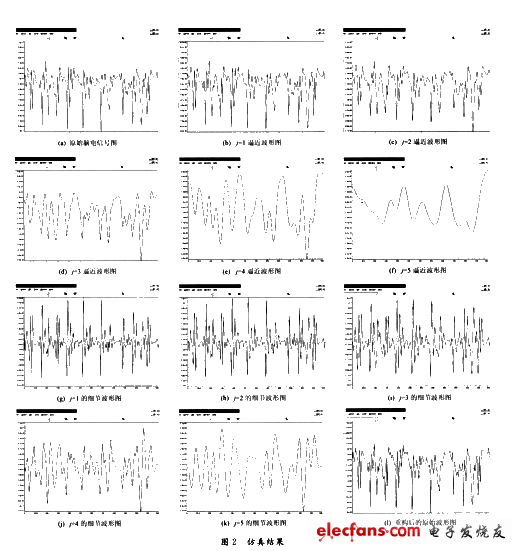
图2(a)为待处理脑电信号，经小波分解后(b)～(f)依次为各级逼近波形图，(g)～(k)则依次为对应的细节波形图。滤掉j=3的细节波形即图2(i)，再进行小波重构后得到图2(1)，从中发现，原图2(a)和重构后的图2(1)几乎看不出明显差别。

4 结 语

本文利用了DSP快速数据处理的优点，采用性价比高的定点型TMS320C54x DSP进行浮点数据处理，结果表明，处理方法可行，效果明显，文中介绍的方法具有一定的理论和实际应用价值。