摘要：介绍智能车竞赛中电磁组的设计思路，论述了基于变参数的PD算法的信号处理方法；分析了传感器布局对转角的影响，提出直接采集交流信号的寻迹方案，并验证了该方案的效果。实验表明：该处理方法实现简单，能够比较精准、快速地跟踪通电导线的轨道。

关键词：磁场；智能车；传感器；PD算法

1 设计原理

1．1 磁场理论

根据麦克斯韦电磁场理论，交变电流会在周围产生交变的电磁场。智能车竞赛使用路径导航的交流电流频率为20 kHz，产生的电磁波属于甚低频(VLF)电磁波。交变磁场分析复杂，并且赛道导航电线和小车尺寸远远小于电磁波的波长，电磁场辐射能量很小，能够感应到电磁波的能量也非常小。所以可将导线周围变化的磁场近似地看作缓变的磁场，按检测静态磁场的方法获取导线周围的磁场分布，进行位置检测。

由毕奥一萨伐尔定律可知，通有稳恒电流I、长度为L的直导线周围会产生磁场，距离导线距离为r处的磁感应强度为：

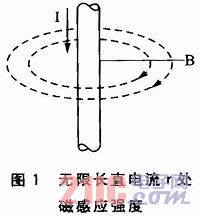
1．2 寻迹原理

基于不同物理效应的磁测量传感器很多，要根据被检测磁场的性质和要求，使用不同的磁场传感器。感应线圈对磁场的变化灵敏度较高，同时也可根据被测磁场的形态和分布选定线圈形状和几何尺寸。选用灵敏度更高的线圈作为识别信号的传感器。

本设计中导线通过的电流频率为20 kHz，且线圈较小。设线圈中心到导线的距离为r，并认为小范围内磁场分布是均匀的。再根据图1所示的导线周围磁场分布规律，利用法拉利定律，线圈中感应电动势可近似为：

即线圈中感应电动势的大小正比于电流的变化率，反比于线圈中心到导线的距离。故导线左右两端传感器的电压值可表示为：

式中，(l1+l2)为定值，计算出的pos值为以传感器轴中心为坐标原点的赛道位置值。

2 磁导航智能车系统

磁导航智能车系统主要分为主控模块、路径信息采集模块、电机驱动模块和电源模块等。磁导航智能车结构框图如图2所示。

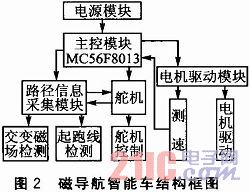
系统磁场环境为埋设在跑道中通过20kHz、100 mA交变电流的导线产生的交变磁场。

3 赛车布局分析及硬件电路

3．1 传感器布局

根据感应线圈安放位置的不同，可将感应方向分解为各分量。如图3所示，当线圈为水平安置时，线圈中检测到的主要是水平方向的磁场分量；线圈为垂直安置时，线圈中检测到的主要是垂直方向的磁场分量。通过对不同方向磁场分量的检测，可以获得磁场的强度和方向。

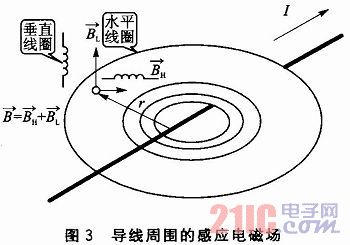
当线圈为水平安置时，检测到的感应电动势如图4所示。磁场强度B是距离x的偶函数，并且在Y轴两侧单调。当线圈为垂直安置时，检测到的感应电动势如图5所示。磁场强度B是距离x的奇函数，但在Y轴两侧没有单调关系。

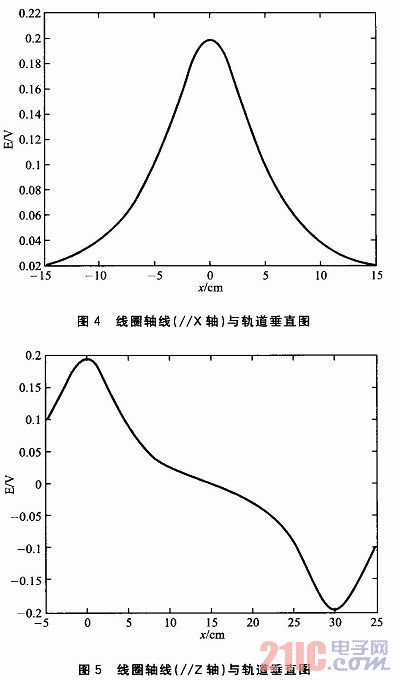
系统采用的是水平安置的方法，主要利用其单调性，软件分析更直观。设计初期，选用了单排水平安装方式1，如图6所示。

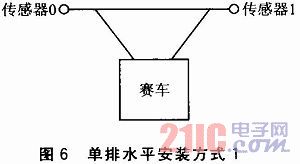
在如上布局中，只通过两端传感器的电压差来计算赛车的位置，赛车就能完成基本任务。

优势：信号采样时间短；系统的实时性好，对微小变化反应及时；算法简单，控制灵活。

劣势：因线圈在磁场中的磁感应强度会受与导线的夹角影响，使得传感器在不同位置获得的电压差值相同，造成误识别；转角不够平稳。为了解决上述问题，提出了增多传感器的方案，传感器的安装方式2如图7所示。

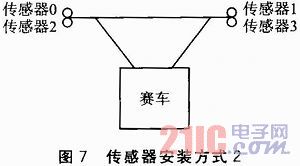
传感器0和2、传感器1和3分别成一定角度固定在赛车前方30 cm的两侧。这样有效地避免了在大S等赛道上因夹角造成的丢线问题。但速度仍受限。

笔者从布局和算法两方面入手。进一步改进，传感器安装方式3如图8所示。

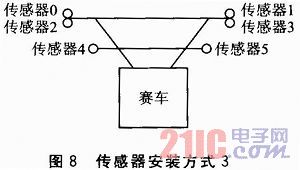
系统采用了双排的传感器排布方案。前排4个传感器，后排2个传感器。传感器0、2与传感器1、3分别位于赛车前方30 cm处，间距为25 cm；传感器4、5分别位于赛车前方20 cm处，间距为20 cm。

两排传感器用法基本相同，位于前排的传感器主要用于对赛道位置的计算；位于后排的传感器用于当小车偏离量比较大时对位置进行辅助控制，同时辅助调节速度。

3．2 信号选频放大

利用电感线圈得到的感应电动势信号太弱，需要对采集后的信号进行放大、滤波处理。对交变信号的识别主要利用的是RLC并联谐振

电路，等效电路如图9所示。

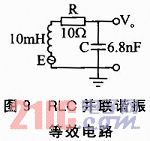
R为电感的等效电阻，E为感应电动势，C是并联谐振电容。电路谐振频率为：

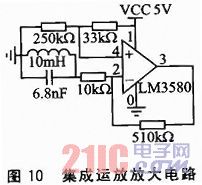
信号放大采用的是集成运放。虽然普通运放的频率响应速度较低，但在实验中发现，放大倍数对信号采集的影响不是很大，只要能够满足采样的电压要求即可。同时，使用集成运放能够有效地隔离电路，引入的干扰少。在实验中，利用集成运放进行半波放大和全波放大，发现全波放大效果更好，灵敏度较高，信号失真较小。集成运放放大电路如图10所示。

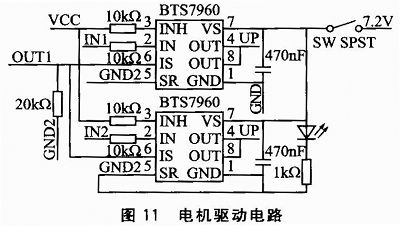
3．3 电机驱动电路

电机驱动电路选用了驱动芯片BTS7960。芯片在工作时，阻抗典型值为16 mΩ(IOUT=9 A，Tj=25℃)，可提供的最大驱动电流为43A。

4 位置分析整体思路

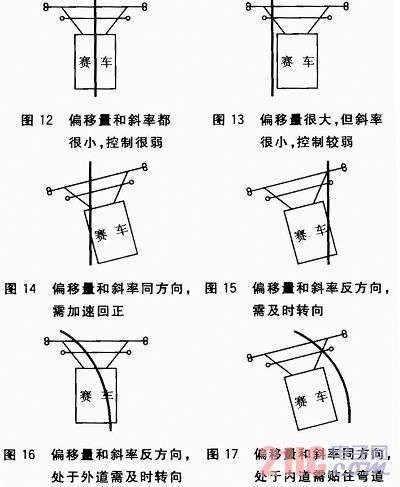
由于电磁寻迹本身的特点，得到的黑线位置是相对精确的模拟量。同时在很大程度上无法预测轨迹位置，借鉴摄像头的弯道半径计算思路，提出双排传感器的角度控制方案。舵机的反馈控制量选用智能车前方20 cm处赛道的斜率以及第一排传感器的偏移量。在实际的跑道中，赛车的偏移量、斜率以及转向的关系如图12～17所示。

4．1 数据采集

系统的主控芯片选用的微控制器是Freescale公司的MC56F8013。因为要直接采集正弦波的交流信号，而该信号的频率为20 kHz，根据采样定理：当fs.max大于信号中最高频率fmax的2倍时，采样之后的数字信号完整地保留了原始信号中的信息。系统直接利用主控芯片的片内晶

振，主频为32 MHz，A／D采样频率最大可达到2．67MHz，该系统通过分频将A／D的转换频率定为200kHz。

因采集得到的数据量较大，在处理方便且不丢失有效信号的原则下，系统仅使用信号中的最大值。为了减少最终误差，在每个处理周期，选取其中的最大值及次大值的平均值作为采样值。

4．2 数据处理

4．2．1 PD算法

在PID控制算法的基础上，选用了增量型的PID控制算法。所需公式为：

△U(k)=Kp·[e(k)-e(k-1)]+Ki·e(k)+Kd·[e(k)-2e(k-1)+e(k+2)] (8)

式中，△U(k)表示增量；e(k)为系统的控制偏差；Kp为比例增益；表示积分系数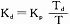；表示微分系数。

本设计去掉了PID中的积分环节，采用了变参数的PD控制器。因积分环节主要是用于消除静态误差，相对于干扰较大的舵机控制来说，它的作用并不明显，反而会降低响应速度。

4．2．2 软件设计

系统中，主要计算赛车位置的是前排传感器。通过左右两端传感器的电压来判断赛车与轨道的距离，利用差值来判断赛车偏离轨道的程度，并计算得到赛车的转角。

在压差求解中，主要利用的是左、右两端各自的传感器检测得到的电压值进行权值可变的加权。权值的变化与当前传感器采集到的电压值相关联，这样有效地避免丢失信号及误差。

AD N=AD maxN0[2]·l1+AD_maxN1[2]·l2 (9)

式中，AD_N是左或右端获得的电压值，AD_maxN0[2]、AD_maxN1[2]是一个周期中该端传感器0、1电压的最大值和次大值的平均值；l1、l2是传感器0、1此时采用的权值。

数据处理部分采用变参数的PD算法。软件设计初期，仅对最后送入舵机的转角采用了PD算法。相比仅简单利用压差计算转角，在小S弯道处赛车运行更连续、更加稳定。中期进行了改进，增加了前排传感器的压差值的PD运算，进一步提高了赛车的连续性。上述两次PD算法的参数由前排压差值及前排和后排的传感器压差得到的斜率而确定。

由于直接输出θ角对应的PWM波进行转角控制，需要建立角度与PWM占空比的精确数学关系，在实际操作中很难实现。在末期，对转角引入了增量逐次逼近控制算法。

具体做法是利用取平均值的方法将通过上述方法所得的6次转角取平均值，同时利用求得的需要输出角度与上次输出角度的差值，引入一个D环节，经过计算后得到的角度作为实际输出。经过多次实验证明，采用这种方法在直道和S弯道时可以避免频繁的大角度修正，减小系统过冲，使行驶更平稳。采用逐次逼近和PD算法的方法实现智能车转弯控制，降低对模型精确度的要求，更好地满足智能车的容错能力。

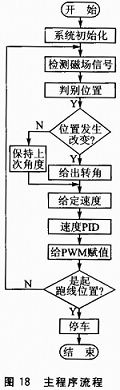
系统主程序流程如图18所示。

结语

实验结果表明，该导航方法满足竞赛要求，采用该方法的赛车在第五届“飞思卡尔”杯全国大学生智能汽车邀请赛上获得全国一等奖。

但该方法中，由于磁传感器检测到的始终是当前位置与导航线之间的相对位置信息，前方路径信息受局限，所以下一步需要考虑赛车的前瞻性，进一步提升赛车速度。