摘要：在智能车传统PID、PD控制的基础上进行改进，提出了一种更为稳定快速的循迹控制方法。智能车的方向控制和速度控制都具有非线性、大滞后的特点，传统的控制方法存在着响应时间不够及稳态误差大的缺点。通过电磁传感器的合理设计，对路径信息和车体状态进行检测，并在此基础上引入基于模糊控制的变参数PD控制和变结构控制。实验结果表明，与传统方法相比，智能车运行的稳定性和快速性都得到了很大的提高。

关键词：智能车；MC9S12XS128；模糊控制；变参数PD控制器；变结构控制器

本文是以第五届“飞思卡尔”杯全国大学生智能汽车竞赛为背景。本届比赛新增加了电磁组的比赛，在50 cm宽的赛道中心铺设有直径0．1～0．3 mm的导线，其中通有20 kHz，100 mA的交变电流。除此之外，在赛道的起跑线处还有永磁铁标志起跑线的位置。车模要通过自动识别导线所产生的电磁场进行路径检测。

从道路元素来看，赛道一般可以分成直道、转弯、S道、回环道等形式。在智能车行驶的过程中，为了选择最佳路径，减少行驶距离，在转弯处最好选择内切，小S弯甚至可以近似的走成直线。但是由于电磁传感器的局限性，不可能像摄像头一样检测到前方赛道的全貌，这就要求在算法上有所突破。

1 智能车系统的硬件组成

1．1 整体硬件结构介绍

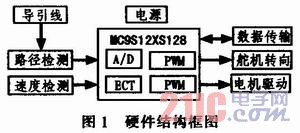
图1所示为智能车控制系统的硬件框图。系统采用飞思卡尔半导体公司的16位微处理器MC9S12XS128作为核心控制芯片，设计最小系统模块；外围电路包括路径检测模块，速度检测模块，舵机转向模块，电机驱动模块；电源模块为整个系统提供动力支持。其中速度检测模块采用光电编码器采集信号，并通过微控制器的ECT模块进行脉冲捕捉计数，测得速度值；电机驱动采用H桥，可实现电机的正反转及制动。

1．2 电磁传感器的设计

根据麦克斯韦电磁场理论，交变电流会在周围产生交变的电磁场。本智能车选用工字型10 mH电感作为磁场感应传感器。这类电感体积小，Q值高，具有开放的磁芯，可以灵敏的感应周围交变的磁场，产生响应感应电动势。图2所示为路径检测模块电路图，这里只为其中的一路。

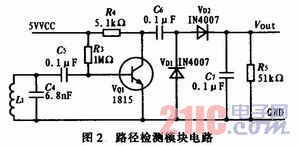
电路中L1为10 mH电感；C4为6．8 nF的谐振电容，实现20 kHz信号的选频电路；Vout为感应电动势输出端。传感器模块伸出车体约10 cm，距离地面8 cm。

由毕奥-萨伐尔定律知，通有稳恒电流的直导线周围会产生磁场，感应磁场分布是以导线为轴的一系列同心圆。圆上磁场强度大小相同，并随着距离导线的径增加成反比下降。

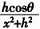通电导线周围的磁场是一个矢量场。在本设计中，根据法拉第电磁感应定律，感应电动势可近似为：。k为比例系数，与线圈摆放方法、线圈面积和一些物理常量有关。感应电动势的方向可用楞次定律来确定。对于放置在导线上方h处，与导线水平距离为x的线圈中产生的感应电动势的大小与成正比。θ是传感器所在平面与导线的夹角

图3所示为车模与赛道位置示意图，车体前部即为路径检测模块。α为车体相对于导线的偏移角度，d为车体相对于导线的偏离距离(垂直与车体中心线的横向距离)。在车模行驶的过程中，每个电感线圈距离导线的距离不同，夹角也不同，因此输出的感应电动势大小不同。

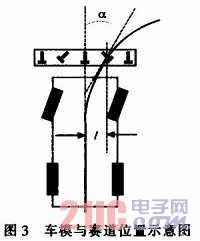
图4所示为本设计中电磁传感器的布局。每两个轴线相互垂直的电感作为一组传感器，水平放置。

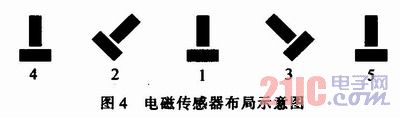
设每组传感器中，前端电感输出的感应电动势为Ey，后端电感输出的感应电动势为Ex，则：

1)对于1号位的两个电感，计算，可求得电感所处磁场的导线方向，即车体相对于导线的偏移角度α；

2)2，3号位的电感同车体中心线成45°夹角，用来确定α值的正负，即导线所处的象限。当2号位检测到的磁场强度明显大于3号位时，以2号位前后两个电感的电动势之比作为方向的参考：当时，α为负(导线处于第二，四象限)，时，α为正(导线处于第一，三象限)；3号位的判别方法与之相反。

3)计算1号位前后两个电感感应电动势平方和之根，再乘以比例系数λ，得到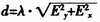，即为车体偏离导线的距离。

4)4，5号位的电感用来辅助判断d值的正负(左为负，右为正)，方法同导线方向的判别类似。

由于实际赛道中磁导线的电流在50～100 mA之间，因此每次上电智能车都要有一个15 s的自学习的过程：将车体贴近赛道做左右摆动(不超出赛道范围)，检测出不同的车体姿态下电感感应电动势的极值，并由此确定值。实验测得传感器模块距离的检测精度为1．5 cm，角度的检测误差在±5°范围内，前瞻距离可达到25 cm。实验的结果表明，这样的传感器布局对于导线的检测是比较准确的，而且它可以预测出导线的方向趋势，便于前瞻性控制算法的设计。

2 整体控制系统的设计

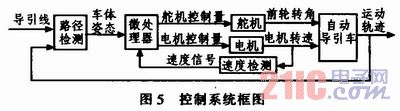
智能车的控制结构是以微处理器为核心。电机控制量、电机转速和速度检测构成一个闭环，该闭环的输入为路径检测后微处理器给定的速度值，输出控制后轮驱动；舵机控制量构成一个控制系统通道，其输入为徽处理器给定的转角值，输出控制前轮转向：最后以运动轨迹作为路径检测反馈控制器的输入，其与导线比较确定车体姿态从而构成一个大的闭环控制系统。智能车的控制系统框图如图5所示。

3 转向控制算法的设计

对舵机的控制，要保证在任何情况下，总能给舵机一个合适的偏移量，保证小车能始终连贯地沿导引线行驶，防止出现大的抖动。

舵机转向是一个双输入单输出的控制器：输入量为偏移角度α及偏离距离d，输出量为舵机的给定值。通过实验得出，系统可以依靠单个输入量来完成控制的舵机，譬如以偏移角度α作为输入，不考虑偏离距离d的作用。这种情况下系统虽然能够运行，但是控制的精度及响应速度较低。同样，在仅依靠偏离距离d的时候，系统的稳定性较差，会出现比较明显的抖动。因此，需要综合分析这两个输入量之间的耦合关系，实现更为精确的控制。

3．1 基于模糊控制的变参数PD控制器

基于模糊控制的PID参数整定就是将模糊理论应用到PID 3个参数的整定中，将模糊理论与PID控制结合起来，构成一个模糊PID控制器。本设计去掉了PID中的积分环节，采用基于模糊控制的变参数PD控制器。因积分环节主要是用于消除静态误差，相对于干扰较大舵机控制来说，它的作用并不明显，反而会降低响应速度。变参数PD控制器的结构如图6所示。图中：rin为系统的输入；yout为系统的输出；error为系统输入与输出的差；ec为误差的变化率。

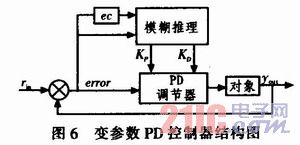
为了实现变参数PD控制，算法引入了两个新的变量：偏移角度的变化率△α和偏移距离的变化率△d。

3．2 模糊控制规则及参数的整定

在模糊控制中取误差α(或d)和误差变化率△α(或△d)为输入语言变量，以构成一个二维模糊控制器，每个语言变量取负大(NB)、负中(NM)、负小(NS)、零(Z)、正小(PS)、正中(PM)、正大(PB)七个语言值。根据各模糊子集的隶属度赋值表和各参数模糊控制模型，建立转向模糊规则表。

参数的调整就是寻求Kp、KD与△α、△d之间的关系。智能车在运行中不断检测α、d和△α、△d，然后查询模糊规则表选择合适的Kp、KD参数进行控制。实际控制中，当△α，△d增大时，表明车体有偏离导线的趋向，这时候增加Kp、KD，阻止车体的继续偏离；当△α，△d减小时，表明车体正逐渐趋近于导线，这时候就要减小Kp、KD。

设计中，系统首先采用基于模糊控制的变参数PD控制器分别实现单个输入量下的控制量输出，然后实验得出的线性耦合关系将两个输出量耦合为一个量控制舵机。

图7所示为转向控制算法框图。UA为纯偏移角度控制时舵机的给定量，UL为纯偏离距离控制时舵机的给定量，SG为最终的舵机给定量。通过实验得到的耦合关系为：SG=0．6UA+0．4UL。这时的舵机响应速度快，直道的跟踪效果很好，通过弯道时可以看到比较明显的内切。

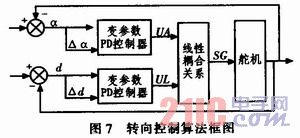
4 速度控制算法的设计

智能车要完成起动、加速、减速、制动等动作。直线行走、拐弯和停车时要求不同的车速，因此速度必须采用闭环控制。智能车的速度与转向是两个独立的被控量，但它们都是根据偏移角度α及偏离距离d来确定输出给定量的。

根据智能车速度控制的特点，设计采用了变结构控制方法。变结构系统是指在控制过程(活瞬态过程)中，系统结构(或叫模型)可发生变化的系统。变结构控制对加给系统的摄动和干扰有良好的白适应性。对于车速的控制，当偏差较小时，采用PID控制，提高稳态精度；当偏差较大时，采用PD控制，以便加快响应速度；当偏差大于可调节范围时，采用Bang-Bang控制。图8所示为速度控制算法框图。

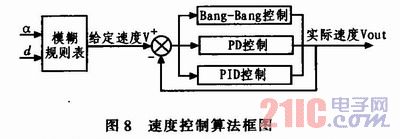
不同的偏移角α及偏离距离d通过查询速度模糊规则表得到给定速度等级V。系统实时检测电机的实际速度值，同当前的设定值做比较，根据误差范围的不同分别采用PID控制、PD控制和Bang-Bang控制。当速度误差在±5％时采用PID控制；当速度误差在±5％～±10％时采用PD控制；当速度误差大于±10％时采用Bang-Bang控制。

5 结论

基于电磁传感器的智能车的设计，可以检测出车模相对于导线的偏移角度α及偏离距离d，并以此作为控制的输入量。通过变参数的PD控制和变结构控制分别实现舵机和电机的精确控制。整体调试后车模速度由传统控制方法下的1．8 m／s提高到目前的2．3 m／s，转弯处可以看到比较明显的内切。实验结果表明，这种控制方法相对于单一的PID控制具有响应时间快，稳态性能好，抗干扰能力强的特点。