摘要：两轮自平衡智能车要求车模两轮驱动实现其直立行走。直立车的硬件设计和软件设计与四轮车相比更加复杂，在“飞思卡尔”杯全国大学生智能汽车竞赛中，直立车故障多，近一半的参赛队伍完不成比赛。直立自平衡智能车主要简化为倒立摆模型，把倒立摆理论引入并通过PID控制，能得到良好的控制效果。

0 引言

近年来，国内外有很多关于两轮自平衡直立电动车的研究，甚至已经生产出相应的代步产品。随着现代科技的发展，对于自平衡的响应速度和精确度提出了更高的要求。“两轮自平衡直立车”的制作，其核心技术就是自平衡系统的开发。直立车模可以简化成倒立的单摆模型。通过传感器获得角速度和角加速度的值，运用PID控制算法实现对其的控制。

1 理论分析

1.1 倒立摆理论模型分析

首先，直立智能车若只直立在原地可以简化成一级倒立摆模型，我们可以从单摆入手，对单摆受力分析如图1所示。

F=-mgsinθ (1)

根据受力分析，当单摆受外力拉离平衡位置时，会受到mgsinθ作用使单摆能够回复到平衡位置，而空气中的阻尼力与mgsinθ的合力驱使单摆稳定在平衡位置，合力越大，单摆稳定得越快，所受干扰的影响也就越小。

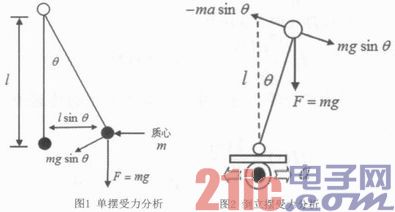
直立的车模可以看成是倒放在可以移动的车轮上的单摆，由于车轮与车体存在相对加速度，因此在非惯性系下分析车模的受力情况，对倒立摆模型受力分析如图2所示。

车模除了受重力的分力mgsinθ外，还受额外的惯性力-macosθ和空气的阻力，因此倒立摆所受的恢复力(此处不计空气阻力)为：

F=mgsinθ-macosθ (2)

由于θ较小，因此可以进行线性化。

为使倒立摆能够稳定下来，而且由于空气的相对阻尼力较小，还应对系统施加额外的阻尼力，因此式(2)可变为：

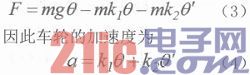
式中θ为车模倾角，θ'为车模的角速度，k1、k2为比例系数。

1.2 直立车系统稳定性分析

对直立车模进行数学建模，依据自动控制理论分析车模通过闭环控制保持稳定的条件。

将直立车模简化为放置在可以左右移动的车轮上的简单倒立摆。假设外力干扰引起车模产生角加速度x(t)。沿着垂直于车模地盘方向进行受力分析。

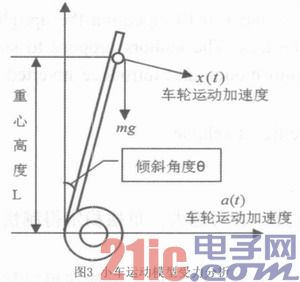
由图3推导出车模倾角与车轮运动加速度a(t)以及外力干扰加速度x(t)之间的运动方程

由式(10)可以看出，当k1≥g，k2≥0时，满足系统稳定的条件，此时直立车模可以稳定。

2 直立智能车系统设计

2.1 硬件电路设计

在上面介绍了车模直立控制数学模型，车模倾角以及倾角速度的测量成为控制车模直立的关键。车模倾角和倾角速度的测量可以分别通过加速度传感器和陀螺仪实现。

2.1.1 三轴加速度计

三轴加速度计可以测量智能车倾角的加速度。直立车模所采用的是加速度传感器MMA7361。该传感器体积小、质量轻、测量精度高、抗干扰能力强、性价比高，MMA7361可以同时输出3个方向上的加速度模拟信号。

2.1.2 陀螺仪

我们选用了村田公司出品的ENC-03系列的陀螺仪，陀螺仪可以测量智能车倾角的角速度。但是此款陀螺仪有一点缺陷是温飘过大，需要我们在软件中进行补偿。

2.2 系统软件设计

通过三轴加速度计和陀螺仪模块分别检测车模的角度和角速度，这似乎只需要加速度计就可以获得车模的倾角，再对此信号进行微分便可以获得倾角速度，但在实际车模运行过程中，由于车模本身的震动和摆动等因素所产生的加速度会产生很大的干扰信号，它叠加在测量的加速度信号上使得输出的信号无法准确反映车模的角度，这些噪声可以通过数据平滑滤波将其滤除，但是平滑滤波一方面会使信号无法实时反映车模倾角变化，减缓对车模车轮的控制，另一方面也会将车模角速度变化信息滤掉，上述两方面的滤波效果都使得车模无法保持直立。

角速度传感器陀螺仪输出的车模角速度受到车体振动的影响小，因此车模的角度可通过对角速度积分得到。但如果角速度信号存在微小的偏差和漂移，经过积分运算之后形成累积误差，这个误差会随着时间延长逐步增加，最终导致电路饱和，使角度信号存在偏差。为消除角速度积分产生的累积误差，利用加速度计获得的角度信息对此进行校正，使积分的角度逐步跟踪到车模运行的真实角度。如下图4所示为车模直立控制算法框图。

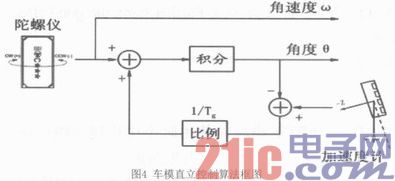
最后，采用PD算法控制车模直立。其公式为

nSpeed=CarAngle*P+CarGyro*D (11)

式中nSpeed为车模速度输出值，CarAngle为车模角度，CarGyro为车模角速度，P为比例参数，D为微分参数。

3 结语

两轮智能车控制系统是一种典型实时精确控制、且自身不稳定的随动控制系统。本文详细介绍了两轮自平衡小车的直立控制原理及设计，包括加速度传感器使用电路及方法、通过角度传感器的反馈量实现小车的平衡控制方法;加速度计和陀螺仪等传感器的选取;硬件电路的设计方法、软件算法的主要控制程序等，可靠稳定地使小车达到2.2m/s。