摘要：在汽车底盘测功机研究中，由于汽车底盘测功机是一个复杂的时变非线性、大惯性系统。传统的PID控制对于非线性、时变性的系统难以达到控制精度的要求，而模糊自适应PID控制具有在线自动调整的功能，从对传统的PID与模糊自适应PID比较的基础上，分析了参教对系统性能的影响，并利用MATLAB软件中的模糊工具箱对连续系统进行了仿真，离散系统采用编程仿真，比较结果表明，模糊自适应PID控制器具有良好的跟踪性能，超调量小、控制精度高、调节速度快，可以实现对PID参数的最佳调整。

关键词：模糊控制；自适应PID；MATLAB；SIMULINK

智能PID控制器把古典的PID控制与先进的专家系统相结合，实现系统的最佳调整。这种控制必须精确的确定系统的模型，首先将操作人员长期实践积累的经验知识用控制规则模型化，然后运用推理可对PID参数实现最佳调整。

文中在汽车底盘测功机控制的基础上，针对常用的工业对象模型，该系统模型具有变参数、强干扰、大滞后等特点，将模糊控制与自适应PID控制相结合，设计了模糊自适应PID控制器，能够实现对kp、ki、kd的自动在线调整。其仿真结果表明模糊自适应PID控制系统性能优于PID控制，且具有响应时间短，控制精度高，超调量小，稳定性好等优点，能够适应复杂对象的要求。

1 模糊自适应PID控制器

1．1 PID控制原理

PID控制系统原理如图1所示。将偏差的比例、积分和微分通过线性组合构成控制量，对被控对象进行控制。

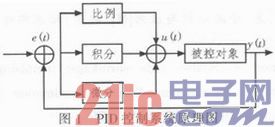
对于连续时间类型，PID控制系统的标准方程为：

式中，u(t)为PID控制器的输出，t为采样时间，kp为控制器的比例增益；e(t)为PID控制器的偏差输入，即给定值与测量值之差；TI为控制器的积分时间常数；TD为控制器的微分时间常数。

1．2 模糊自适应PID控制器原理

自适应模糊PID控制器是以误差e和误差的变化率ec作为输入，可以满足不同时刻的e和ec对PID参数自整定的要求。其结构图如图2所示。

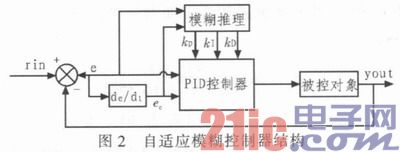
从系统的稳定性、响应速度、超调量和稳态精度等各个方面来考虑，kp、ki、kd的作用如下。

1)比例系数kp的作用是加快系统的响应速度，提高系统的调节精度，kp越大，系统的响应速度越快，系统的调节精度越高，但易产生超调，甚至会导致系统不稳定。

2)积分系数ki的作用是消除系统的静态误差。ki越大，系统的静态误差消除的越快，但ki过大，在响应过程的初期会产生积分饱和现象，从而引起响应过程的较大超调。

3)微分作用系数kd的作用是改善系统的动态特性，其作用主要是在响应过程中抑制偏差向任何方向变化，对偏差变化进行提前预报。但kd过大，会使响应提前制动，从而延长调节时间，而且会降低系统的干扰性能。

1．3 模糊自适应PID控制系统的设计

设计模糊自适应PID控制系统的核心是设计模糊控制器，在设计模糊控制器的过程中，确定模糊控制器的结构、建立模糊规则并选定近似推理算法是两个核心工作，与之配套的是设计模糊化模块、选择模糊子集的隶属度函数、设计清晰化模块并选择清晰化方法。其中根据积累的人工操作经验或测试数据，建立模糊控制规则是设计最为核心的工作。

1．3．1 量化因子和比例因子

量化因子和比例因子除了进行论域变换，使前后模块匹配之外，在整个系统中还有一定的调节作用。因为它的变化相当于对实际测量信号的放大或缩小，直接影响着采样信号对系统的调节控制作用。文中为了便于比较模糊自适应PID与经典的PID控制效果，将kp、ki、kd 3个因子不再变化，而是通过改变模糊论域和量化因子、比例因子的方法改变输出量。

1．3．2 模糊论域及隶属度函数的确定

E为输入误差e的语言变量，EC为误差变化率的语言变量。{-3，-2，-1，0，1，2，3}为E和EC的论域，它们的模糊子集为{NB(负大)，NM(负中)，ZO(零)，PS(正小)，PM(正中)，PB(正大)}。它们的模糊子集为{NB(负大)，NM(负中)，ZO(零)，PS(正小)，PM(正中)，PB(正大)}。kp、ki、kd的量化范围为(-0．3，0．3)，(-0．06，0．06)，(-3，3)。其隶属度曲线如图3所示。通过各曲线的比较，隶属度曲线采用双高斯型曲线。kp、ki、kd的隶属度曲线和图3相似，只是论域范围不同。

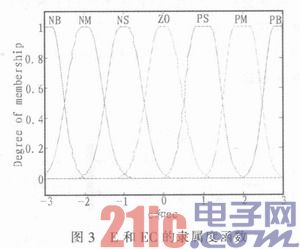
1．3．3 解模糊方法

模糊推理采用广泛应用的Mamdani算法，其合成方式直接采用极大极小运算。本仿真在对其他解模糊方法尝试的基础上，通过比较选出最优方法——最大隶属度中取小方法即som法。

设有n个点的隶属度都取最大值，即A(uj)=max(A(u))，j=1，2，…n，则取绝对值最小的点min(|uj|)=|uk|作为模糊集合的代表点。

1．3．4 模糊控制规则

kp、ki、kd的模糊控制规则表建立好以后，根据模糊论域和隶属度函数可以求出各个子集的隶属度，根据各模糊子集的隶属度赋值表和各参数模糊控制模型，应用模糊合成推理设计PID参数的模糊矩阵表，查表修正参数带入下式计算：

其中，kp'、ki'、kd'为设置的初始值，{ei，eci}p、{ei，eci}i、{ei，eci}d为通过模糊调整后的调整值。参数调程规则表如图4所示。

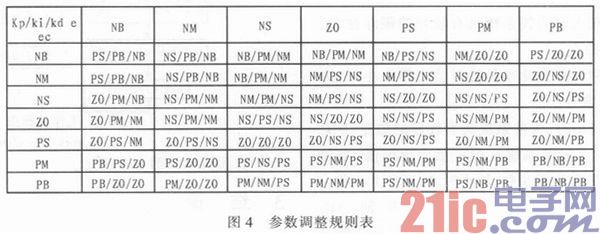
2 模糊自适应PID控制仿真及结果分析

2．1 SIMULINK仿真

打开MATLAB的SIMULINK工具箱，利用SIMULINK内的子模块库设计仿真电路，设计时调整好各个模块的参数，如各种数值算法、仿真时间、仿真步长等。为了便于调整，对其中的部分模块进行了封装，封装成不同的子模块。最后可将结果送入模拟示波器给予显示，或送到工作空间，如仿真结果不满意，可适当调整量化因子和比例因子，再调整模糊规则和隶属度函数。

仿真时采用的系统函数为工业常用的仿真系统，其系统函数为：

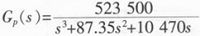
仿真图如图5所示，仿真时间为50 s，是对连续控制系统进行的模拟。仿真前首先在MATLAB的Command Window中输入sub_1=readfis(‘sub_1’)，使模糊控制规则读入到工作空间，然后双击Fuzzy Logic Controller，添加sub_1(模糊控制规则)到模糊逻辑模块。为了便于比较，将模糊自适应PID控制与经典的PID控制在同一模块中仿真。

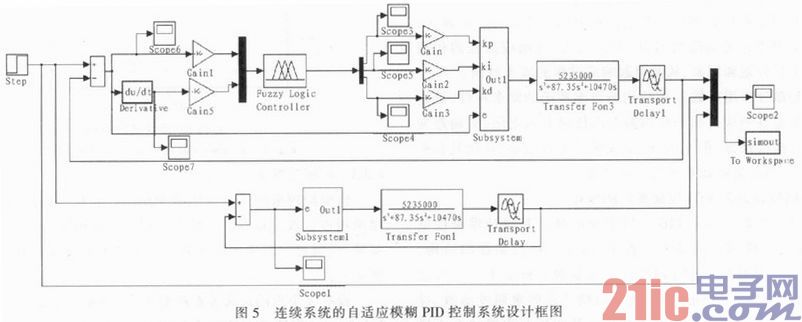
若将系统函数改成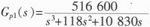：时，并加大延迟时间为2 s，其各控制曲线图如图6所示。

其参数整定原则如下：

1)当误差绝对值较大时为使系统具有较好的跟踪性能，应取较大kp的与较小的kd。

2)当误差绝对值和误差变化率的绝对值中等大小时，为使系统超调较小，kp应取得小。

3)当误差绝对值较小时，为使系统具有较好的稳定性，kp与ki均应取大些，同时为避免系统在设定值出现振荡，当误差变化率绝对值较大，kd可取得小些，较小时，kd可取大一些。

具体调整规则如下：先整定kp、令ki、kd均为零，使kp由小到大，找出最佳响应曲线，确定好kp的最优值，在此基础上将ki有小到大，找出静态误差最小时的最佳ki值，然后，观察曲线的超调量大小，若超调量过大，使kd由小到大逐步调节，边调节边观察超调量的大小，找出最佳的kd，而使超调量最小，若超调量在允许的范围内，可令kd=0，反复上述过程，找出最佳的kp、ki、kd。

2．2 软件编程仿真

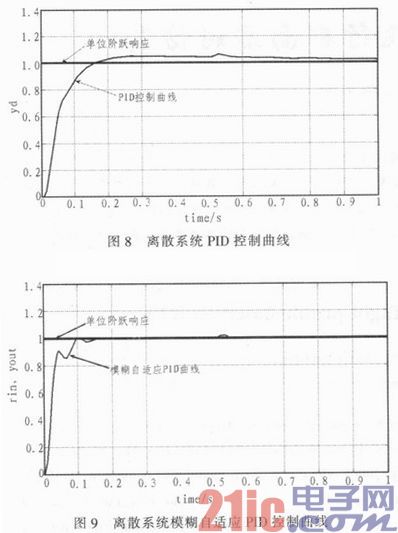
利用MATLAB提供的运行环境，编写M文件，仿真时间为1 s，采样时间为1 ms，将模糊PID控制和PID控制分别进行仿真，在第500个采样时间控制输入加入1．0的脉冲干扰，其工作流程图如图7所示。

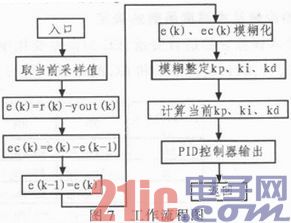
仿真结果如图8，9所示。

3 结论

在经典PID控制的基础上设计了模糊自适应PID控制系统，该系统基于大滞后、时变、非线性等复杂环境，从上图的SIMULINK和软件编程仿真结果可以看出，PID参数的调节对系统的性能影响很大，良好的参数设置使得模糊自适应PID控制器具有响应速度快、超调量小、控制精度高等优点，具有良好的跟踪性能，较好的抗干扰性能，较强的鲁棒性能，可以达到系统控制精度的要求。在控制系统中被广泛应用，为下一步应用于汽车底盘测功机作准备。