地面上铺设载流导线,通以一定频率和幅值的周期性交变电流,作为引导智能车行进的迹线。用大电感作为传感器,配以一定的电路,获得相应的电压。这是一种较新的循迹方式,在第五届“飞思卡尔”杯全国大学生智能车竞赛上出现。目前有两种主要的迹线信息解算方法,一是通过整流滤波之后查表,使电压与距离对应;二是用一排密集电感作为传感器,靠近迹线的电感显高电压,远离迹线的显低电压。由于大赛之前尚无精确的数学模型求解迹线信息,本文将试图向这方面努力。
1.传感器排布与赛道信息解算的数学模型
假设载流导线无限长直,电流为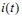 。不妨假设电感为理想电感,即空间尺寸可忽略不计,电感铁芯工作在线性区[1]。
。不妨假设电感为理想电感,即空间尺寸可忽略不计,电感铁芯工作在线性区[1]。
空间一点某一方向上的磁感应强度为 ,由毕奥--萨伐尔定律[2]得
,由毕奥--萨伐尔定律[2]得 ,其中
,其中 由空间位置决定,
由空间位置决定, 。不妨将称
。不妨将称 为空间函数,电感不同的放置方式,对应不同的
为空间函数,电感不同的放置方式,对应不同的 。若迹线为无限长直的导线,则相同的电感放置方式下,
。若迹线为无限长直的导线,则相同的电感放置方式下, 的表达式不变。
的表达式不变。
设 为电感的开路感应电动势,由法拉第电磁感应定律[3]得:
为电感的开路感应电动势,由法拉第电磁感应定律[3]得: ,其中
,其中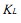 由电感的参数决定,是常数。
由电感的参数决定,是常数。
将 进行拉氏变换得
进行拉氏变换得 ,其中
,其中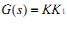 ,
,
将 进行拉氏变换得
进行拉氏变换得 ,其中
,其中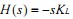 。
。
将电感到A/D转换之间的电路设计为线性时不变系统,设其传递函数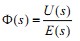 ,则
,则
在小车起跑前测得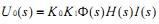 ••••••(1)
••••••(1)
在小车起跑后测得 ••••••(2)
••••••(2)
式(2)除以(1)得
发现电路的传递函数和电流等与空间函数无关的项都被消去了。对于不同的电感排布方式,只要先得出空间函数,然后运用该方法就能得出其对应的迹线信息解算表达式。这也正是本文要做的工作。为方便起见,将该方法称为“法一”。
这种方法有几个优点:一是表达式与电路传递函数无关,即与电路无关,这就使得电路设计从理论上讲极其简单,只需满足线性时不变;二是表达式与赛道电流无关,这就使得该方法推导的模型从理论上讲具有极强的适应性;三是该方法推导的模型运用起来简单高效。
1.1 双一电感测距
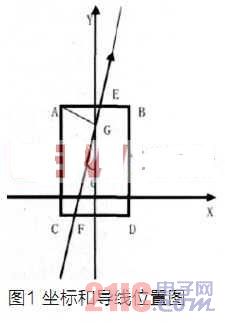
如图1,两电感A和B水平放置,二者轴线与x轴平行,相距 ,离地高度
,离地高度 。记
。记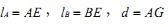 。下面将用到文献[4]的方法,以避免开根号。
。下面将用到文献[4]的方法,以避免开根号。
A电感的变量用下标A表示,B电感的变量用下标B表示。为了方便运用法一,不妨令 。
。
显然 , 易得
, 易得 ,
,
那么 ,其中
,其中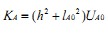
不妨假设 较小,可以忽略。则
较小,可以忽略。则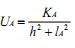 ••••••(3)
••••••(3)
同理得 ,其中
,其中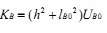 ••••••(4)
••••••(4)
 ••••••(5)
••••••(5)
联立(3)、(4)、(5),解得。注意 是有正负的。
是有正负的。
实验数据如表1。所有单位均为标准点位,电压是示波器读取的峰峰值,误差是未取绝对值的相对误差。
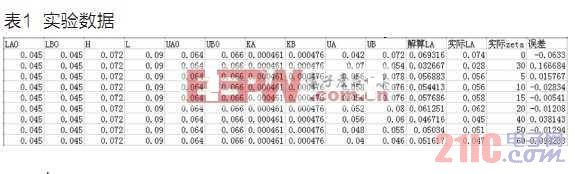
结论:除第二组外,其他组的误差都小于10%,大部分小于5%,且与赛道无明显关系。说明该数学模型正确,同时也佐证了法1.1的正确性。